22. Условие существования оптимального решения задачи линейного программирования

Теорема 1. Пусть исходная задача решается на максимум. Если для некоторого опорного плана все оценки _j неотрицательны, то такой план оптимален. Доказательство. Так как Z= ₀ — и по условию _j0 , то Z достигает максимального значения при =0. Это возможно лишь при x_m+1=0, x_m+2=0, ..., x_n=0, т. е. опорный план (b₁, b₂, ..., b_m, ) оптимален.

Теорема 2. Если исходная задача решается на минимум и для некоторого опорного плана все оценки _j неположительны, то такой план оптимален.

Доказательство аналогично предыдущему случаю.

Сформулированные теоремы позволяют проверить, является ли найденный опорный план оптимальным.

23. Метод прямого перебора решения злп

Метод прямого перебора – метод, когда перебирают угловые точки и подставляют в целевую функцию любое базисное решение системы линейных уравнений (координаты угловой точки). Из них выбираем минимальное.

Если известна функциональная связь целевой функции Y и искомой переменной X, то можно последовательно вычислить значения целевой функции для некоторых значений искомой переменной. Вычисления повторяются до тех пор, пока не будет найден min (max) значения целевой функции

Y=f(x₁, ..., x_i, ..., x_n, u₁, ..., u_j, ..., u_m),

x_i=x_0i+x_ik (k=0, 1, 2, ..., l).

Этот метод может быть использован для решения задач исследования операций, если имеются одна искомая переменная или несколько с небольшим диапазоном изменения искомых переменных.

Особенность и преимущества метода прямого перебора заключаются: 1) в независимости поиска от вида и характера целевой функции; 2) в цикличности поисковой процедуры; 3) в определении глобального экстремума целевой функции; 4) в простоте алгоритма и программы оптимизации; 5) в малом объеме необходимой машинной памяти.

В случае большой области изменения искомой переменной и (или) наличия более чем одного экстремума исследуемой функции использование этого метода неэффективно.

24. Основная идея симплекс-метода решения злп и ее теоретическое обоснование

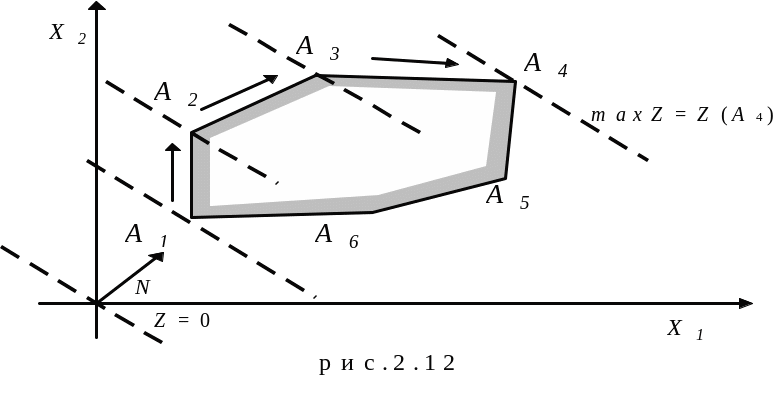
Его суть в следующем. Если известны какая-нибудь крайняя точка и значение целевой функции, то все крайние точки, в которых целевая функция принимает худшее значение, заведмо не нужны. Отсюда естественно стремление найти способ перехода от данной крайней точки к смежной по ребру лучшей, от нее к еще лучшей (не худшей). Для этого нужно иметь признак того, что лучших крайних точек, чем данная крайняя точка, вообще нет. В этом и состоит общая идея наиболее широко применяемого симплексного метода ( метода последовательного улучшения плана) для решения ЗЛП. Итак, симплексный метод предполагает : 1) умение находить начальный опорный план; 2) наличие признака оптимальности опорного плана; 3) умение переходить к нехудшему опорному плану.

Теоретические обоснования симплекс-метода.

Любую ЗЛП можно представить в эквивалентном предпчтительном виде:

max(min) , (2.58)

(2.59)

(2.60)

Выразим базисные переменные х₁, х₂, ..., x_m из равенств (2.59) через свободные х_m+1, х_m+2, ..., x_n и подставим их в целевую функцию. После группировки подобных членов получим

Z=(c₁b₁+c₂b₂+...+c_mb_m)–((c₁a_1,m+1+c₂a_2,m+1+...+c_ma_m,m+1)–c_m+1)x_m+1+(( c₁a_1,m+2+

+c₂a_2,m+2+ ... +c_ma_m,m+2)–c_m+2)x_m+2+...+((c₁a_1n+c₂a_2n+ ... +c_ma_mn)–c_n)x_n (2.61)

Введем обозначения:

₀= c₁b₁+c₂b₂+...+c_mb_m=с_бА₀ ,(2.62)

_j=(c₁a_1j+c₂a_2j+...+c_ma_mj)–c_j= с_бА_j–c_j , (2.63)

где с_б=(c₁, c₂, ..., c_m) — вектор коэффициентов целевой функции при базисных переменных; А₀=(b₁, b₂, ..., b_m)^T —  вектор-столбец свободных членов; А_j=(a_1j, a_2j, ..., a_mj)^T — вектор-столбец коэффициентов при переменных х_j.

С учетом равенств (2.61)—(2.63) задача (2.58)—(2.60) примет вид:

max(min)Z= _{0 –} (2.64)

(2.65)

(2.66)

где₀= с_бА₀ ;_j=с_бА_j–c_j

Задачу (2.64)—(2.66) записывают в таблицу, которая называется симплексной (табл.1). Последнюю строку называют индексной строкой (строкой целевой функции), число ₀= с_бА₀ — значение целевой функции для начального опорного плана х₀, т.е. ₀=Z(х₀). Числа _j=с_бА_jc_j называются оценками свободных переменных.