52. Условный экстремум функции

Условный экстремум функции z = f(x,y) называется экстремум, найденный при условии, что первые x и y связанны уравнением

53. Метод неопределенных множителей Лагранжа.

Можно решить, если все равенства: Z=f(x₁, x₂, ..., x_n) – мах(1)

при ограничениях g_i(x₁, x₂, ..., x_n)=b_i, i=1, ..., m.

Для решения задачи составим функцию

F(x₁, x₂, ..., x_n, ₁, ₂, ..., _m)= f(x₁, x₂, ..., x_n)+ (2)

определим частные производные и приравняем их к нулю. В результате получим систему уравнений

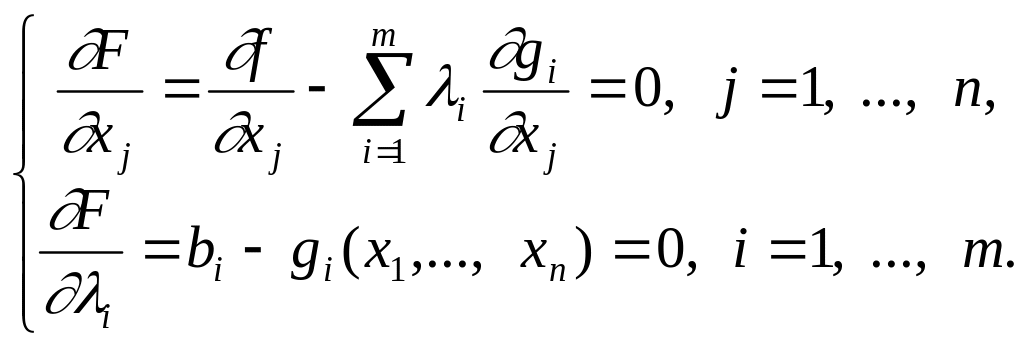(3)

Функция (2) называется функцией Лагранжа, а числа _i — множителями Лагранжа. Если функция Z=f(x₁, x₂, ..., x_n) в точке X⁽⁰⁾=( ) имеет экстремум, то существует такой вектор , что точка является решением системы (3). Следовательно, решая систему (3), получаем множество точек, в которых функция Z может иметь экстремальные значения. Таким образом, определение экстремальных точек задачи (2) методом множителей Лагранжа включает следующие этапы:

1. Составление функции Лагранжа.

2. Нахождение частных производных от функции Лагранжа по переменным x_j и _i и приравнивание их к нулю.

3. Решая систему уравнений (3), находят точки, в которых целевая функция задачи может иметь экстремум.

4. Среди точек, подозрительных на экстремум, находят такие, в которых достигается экстремум, и вычисляют значение функции (1) в этих точках.

54. Определение выпуклой и вогнутой функции

Функция f(x₁, x₂, ..., x_n), заданная на выпуклом множестве X, называется выпуклой, если для любых двух точек X₁ и X₂ из X и любого 01 выполняется соотношение

Функция f(x₁, x₂, ..., x_n), заданная на выпуклом множестве X, называется вогнутой, если для любых двух точек X₁, X₂ из X и любого 01 выполняется соотношение

Если f (X) — выпуклая функция, то –f (X) — вогнутая функция, и наоборот.

55. Общая постановка задачи выпуклого программирования. Теорема о существовании решения задачи вп(формулировка)

Постановка задачи выпуклого программирования.

Рассмотрим задачу нелинейного программирования:

f (x₁, x₂, ..., x_n)max(min) (1)

g_i (x₁, x₂, ..., x_n)b_i (i=1, ..., m), (2)

x_i0 (j=1, ..., n), (3)

ОДЗ (2) обладает свойством регулярности, если найдется такой вектор х_к, что функции g_i (х_к)b_i (i=1, ..., m)ЗНЛП наз-ся задачей выпуклого программирования, если функция (1) либо выпукла, либо вогнута, а все функции g_i выпуклы.

Теорема:любой локальный экстремум задачи ВП является глобальным. (глоб – экстремум на всей ф-ии, лок – экстремум на отрезке ф-ии)

56. Седловая точка функции Лагранжа.

Функция Лагранжа L:

L(x₁, x₂, ..., x_n, y₁, y₂, ..., y_m)= f(x₁, x₂, ..., x_n)+

(только для ЗВП, для других нет смысла)

Седловая точка функции Лагранжа – это вектор [X⁽⁰⁾, Y⁽⁰⁾]:

L( , ) <= L( , ) <= L( , )

57. Теорема Куна-Таккера (формулировка)

Для задачи выпуклого программирования, множество допустимых решений которой обладает свойством регулярности, план X⁰ тогда и только тогда является оптимальным решением, когда существует такой вектор У⁰ (у⁰_i>=0, i=1,m), такой что точка (X⁰, У⁰) — седловая точка функции Лагранжа. Она ведет к системе аналитических уравнеий.

62. Определение сепарабельной функции.

Функция f (x₁,x₂,…,x_n) наз-ся сепарабельной, если она может быть представлена в виде суммы функций, каздая из которых зависит только от одной переменной:

то есть заменяем функцию ломанными линиями

66. Постановка задачи параметрического программирования и принцип ее решения.

Это задача ЛП, в которой либо c_j, либо a_ij не conct, а зависимая от каких-либо параметров.

В общем виде:

t – параметр

Общая идея решения:

1) фиксируют t (t, как правило, задают; )

2) решаем задачу симплекс-методом

3) устанавливаем отрезок , в котором решения сохраняются, то есть находим дельта т.

Фиксируют t₁

70. Связь проблемы выбора с задачами ЛП, НЛП, ИГР.

Задача принятия решений принадлежит к самому распространенному классу задач, с которыми сталкивается человек. Вся наука МО решает задачи выбора. Проблема состоит в нахождении экстремумов целевой функции при наличии системы ограничений и условий неотрицательности некоторых переменных.