32. Леммы и теоремы двойственности (без док)

Исходная задача: найти максимум функции

(2.73)

при условиях

(2.74)

(2.75)

Двойственная задача: найти минимум функции

(2.76)

при условиях

(2.77)

Ле1: Если Х — некоторый план исходной задачи (2.73)—(2.75), а Y— произвольный план двойственной задачи (2.76),(2.77), то значение целевой функции исходной задачи при плане Х всегда не превосходит значения целевой функции двойственной задачи при плане Y, т.е. Z(X)Z^*(Y).

Ле2: Если Z(X^*)=Z^*(Y^*)для некоторых планов X^* и Y^* задач (2.73)—(2.75) и (2.76),(2.77), то Х^* — оптимальный план исходной задачи, а Y^* — оптимальный план двойственной задачи.

Теорема1: (первая теорема двойственности). Если одна из пары двойственных задач (2.73)—(2.75) или (2.76),(2.77) имеет оптимальный план, то и другая имеет оптимальный план и значения целевых функций задач при их оптимальных планах равны между собой т.е. Z_max=Z*_min..

Если же целевая функция одной из пары двойственных задач не ограничена [для исходной сверху, для двойственной снизу], то другая задача вообще не имеет планов.

Теорема2:  (вторая теорема двойственности). План Х^*=(х^*₁, х^*₂, ..., х^*_n) задачи (2.73)—(2.75) и план Y^*=(y^*₁,y^*₂,...,y^*_m) задачи (2.76), (2.77) являются оптимальными планами этих задач тогда и только тогда, когда для любого j выполняется равенство

.

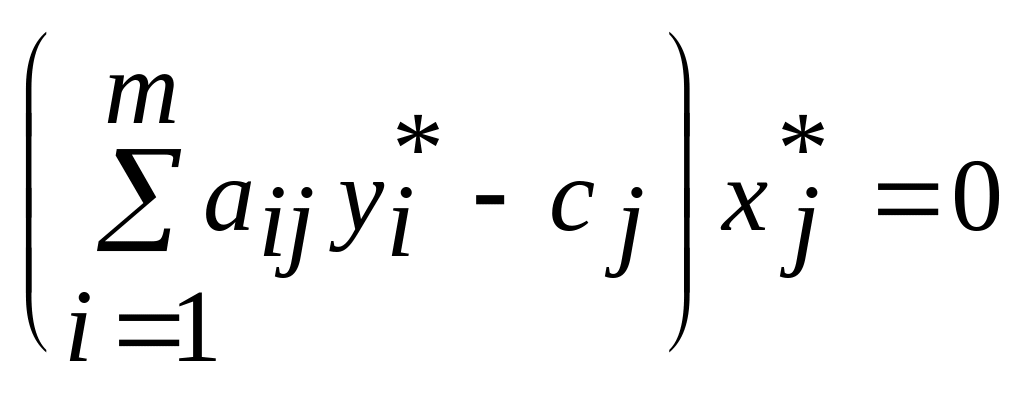33. Применение двойственных задач

34. Связь между решениями прямой и двойственной задачи на примере пары симметричных задач

Исходная задача: найти максимум функции

(2.73)

при условиях

(2.74)

(2.75)

Двойственная задача: найти минимум функции

(2.76)

при условиях

(2.77)

Каждая из задач двойственной пары (2.73)—(2.75) и (2.76),(2.77) фактически является самостоятельной задачей линейного программирования и может быть решена независимо одна от другой. Однако при определении симплексным методом оптимального плана одной из задач тем самым находится решение и другой задачи.

35. Экономическая интерпретация двойственных задач (на примере). Экономический смысл 1-ой теоремы двойственности

Х^* = (х₁^*, х₂^*,…, х_n^*) – план производства

У^* = (у₁^*, у₂^*,…, у_n^*) – набор цен оказался оптимальным, тогда прибыль от продукции, найденная при «внешних» (известных заранее) ценах с₁, с₂,…, с_n равна затратам на ресурсы при «внутренних» (определенными только из решения задачи) ценах у₁, у₂,…, у_m.

Для всех других планов х и у обеих задач прибыль от продукции всегда меньше или равна затратам на ресурсы.

36. Оптимальные двойственные оценки и их смысл в задаче об использовании ресурсов.

Компоненты оптимального решения двойственной задачи наз-ся оптимальными двойственными оценками исходной задачи (скрытые доходы). Они определяют степень дефицитного ресурса. Числовое значение двойственной оценки показывает, на сколько единиц вырастает прибыль при увеличении запаса данного ресурса на 1.

Перераспределение оптимального плана производства можно взять из соответствующего столбца симплекс-таблицы.

Ненулевые значения доп. У показывают, что производить данный вид соответствующей продукции – выгодно.