38. Метод искусственного базиса

Если ограничения ЗЛП можно преобразовать к виду AXA₀ при А₀0, то система ограничений всегда содержит единичную матрицу. Многие ЗЛП, имеющие решения, не содержат единичной матрицы и не приводятся к указанному виду. В этом случае для решения задач применяется метод искусственного базиса. Рассмотрим общую ЗЛП.

Найти минимальное значение линейной функции Z=C₁x₁ + C₂x₂ + ... +C_nx_n при ограничениях

где b_i  0 и система ограничений не содержит единичной матрицы. Для получения единичной матрицы к каждому равенству прибавим по одной переменной х_n+i  0 (i=1,2,..., m), которые назовем искусственными, и рассмотрим расширенную задачу, связанную с отысканием наименьшего значения линейной функции при ограничениях

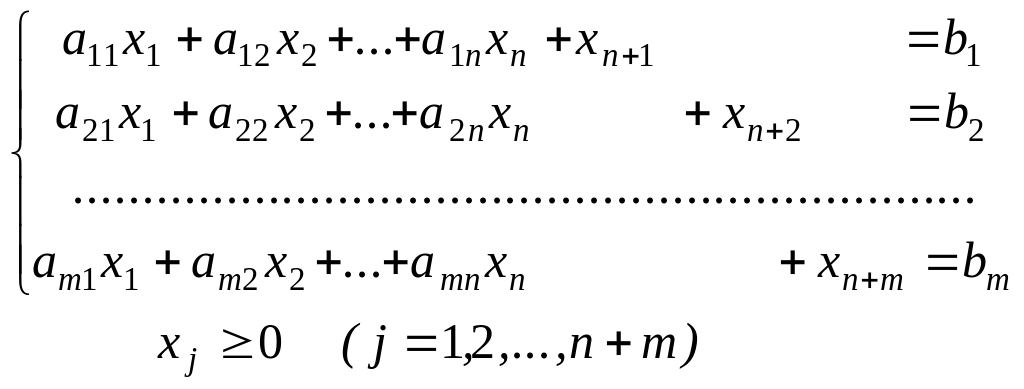
Величина М предполагается достаточно большим положительным числом, если задача решается на отыскание минимального значения линейной функции, и достаточно малым отрицательным числом, если находится максимальное значение линейной функции. Единичные векторы A_n+1, A_n+2, ..., A_n+m, соответствующие искусственным переменным, образуют искусственный базис.

39. Основные понятия теории игр

Теория игр представляет собой математическую теорию конфликтных ситуаций. Ее цель — выработка рекомендаций по разумному поведению участников конфликта.

Конфликтными называются ситуации, в которых сталкиваются интересы двух (или более) сторон, преследующих разные (иногда противоположные) цели, причем выигрыш каждой стороны зависит от того, как себя поведут другие.

Каждая непосредственно взятая из практики конфликтная ситуация очень сложна и ее анализ затруднен наличием многих несущественных факторов. Чтобы сделать возможным математический анализ конфликта, строится его математическая модель. Такую модель называют игрой. От реального конфликта игра отличается тем, что ведется по определенным правилам.

конфликтующие стороны условно называются игроками, одно осуществление игры — партией, исход игры — выигрышем или проигрышем.

В игре могут сталкиваться интересы двух или более участников; в первом случае игра называется парной, во втором — множественной.

Ходом называется выбор игроком одного из предусмотренных правилами игры действий и его осуществление. Ходы бывают личные и случайные. При личном ходе игрок сознательно выбирает и осуществляет тот или другой вариант действий (пример — любой ход в шахматах). При случайном ходе выбор осуществляется не волей игрока, а каким-то механизмом случайного выбора

Цель — оптимизация поведения игрока в игре, где (может быть, наряду со случайными) есть личные ходы. Такие игры называются стратегическими.

40. Антагонистические игры, седловая точка

Игра называется игрой с нулевой суммой, если сумма выиграшей всех игроков равна нулю (т.е. каждый игрок выигрывает только за счет других). Самый простой случай — парная игра с нулевой суммой — называется антагонистической.

Рассмотрим такую игру, в которой участвуют два игрока А и В, имеющие противоположные интересы: выигрыш одного равен проигрышу другого. Так как выигрыш игрока А равен выигрышу игрока В с противоположным знаком, мы можем интересоваться только выигрышем а игрока А. Цель игрока А — максимизировать свой выигрыш а, в свою очередь, цель игрока В — минимизировать эту же величину, которая является для него проигрышем. Пусть у игрока А имеется m возможных стратегий А₁, А₂, ..., А_m, а у игрока В — n возможных стратегий В₁, В₂, ..., В_n (такая игра называется игрой m  n). Выбор стратегии каждым игроком производится при полном незнании выбора другого игрока. Предположим, что для каждой пары стратегий А_i, В_j выигрыш a_ij нам известен. Тогда в принципе можно составить прямоугольную таблицу (матрицу), в которой перечислить стратегии игроков и соответствующие выигрыши.

Таблица 4.1.

Ai	Bj	B1	B2	...	Bn
A1		a11	a12	...	a1n
A2		a21	a22	...	a2n
...		...	...	...	...
Am		am1	am2	...	amn

Игра, представленная таким образом, называется матричной, а полученная таблица — платежной матрицей. Само по себе приведение игры к матричной форме уже может составить трудную задачу, а иногда и практически невыполнимую из-за необозримого множества стратегий. Заметим, что если игра приведена к такому виду, то многоходовая игра фактически сведена к одноходовой — от игрока требуется сделать только один ход: выбрать стратегию.

Пусть игрок А выбирает некоторую стратегию А_i; тогда в наихудшем случае (например, если выбор станет известным игроку В) он получит выигрыш, равный . Предвидя такую возможность, игрок А должен выбрать такую стратегию, чтобы максимизировать свой минимальный выигрыш  :

 .

Величина  — гарантированный выигрыш игрока А — называется нижней ценой игры. Стратегия А_i, обеспечивающая получение , называется максиминной.

Игрок В, выбирая стратегию, исходит из следующего принципа: при выборе некоторой стратегии В_j его проигрыш не превосходит максимального из значений элементов j-го столбца матрицы, т. е. меньше или равен . Рассматривая множество для различных значений j, игрок В, естественно, выберет такое значение j, при котором его максимальный проигрыш  минимизируется:

 .

Величина  называется верхней ценой игры, а соответствующая выигрышу  стратегия В_j — минимаксной. Нижняя цена игры всегда не превосходит верхней цены игры. Если ==v, то число v называется ценой игры.

Фактический выигрыш игрока А при разумных действиях партнеров ограничен нижней и верхней ценой игры. Игра, для которой =, называется игрой с седловой точкой.

Для игры с седловой точкой нахождение решения состоит выборе максиминной и минимаксной стратегий, которые являются оптимальными.

Стратегии игроков, для которых вероятности u_i и z_i отличны от нуля, называются активными.