Практикуемая математическая модель пространственной засечки

В предыдущем параграфе была рассмотрена модель и ее решение на случай, когда всевозможные погрешности измерений, которые порождаются влиянием атмосферы и погрешностями часов на спутнике и приемнике отсутствуют.

В практике же данные погрешности принимаются в виде составляющих самих величин псевдодальностей и геометрических дальностей. Иными словами они вводятся в уравнения в явном виде.

Поправки за данные погрешности можно учесть с использованием моделей погрешностей, определить их в качестве дополнительных неизвестных в процессе решения переопределенной системы уравнений, можно на некотором этапе искусственно исключить их. Одно при этом остается неизменным фактом – они реально воздействуют на результаты измерений и необходимо тем или иным образом их учитывать.

С учетом сказанного далее приведем детализированную модель пространственной засечки в виде соотношения измеряемых псевдодальностей и геометрических дальностей.

Это те же уравнения поправок, которые рассмотрены в предыдущем параграфе с тем отличием, что далее в них используются обозначения, принятые в литературе по космической геодезии с детализацией этих уравнений дополнительными элементами в виде поправок и неизвестных. Поправки как правило определяются по математическим моделям, а дополнительные неизвестные могут быть добавлены в уравнения по мере необходимости.

В спутниковых технологиях используются измерения двух видов величин: псевдодальности и фазы. Псевдодальность – это расстояние между спутником i и приемником A, получаемое при умножении значения скорости света с на измеренную по показаниям часов спутника и приемника временную задержку в распространении сигнала. Эта задержка искажена ошибками в показаниях часов, влиянием среды распространения, задержками в аппаратуре спутника и приемника и другими факторами, которые в аналитическом представлении задачи рассмотрим, а в практических вычислениях для простоты рассмотрения опустим. Псевдодальности измеряются по сигналам точного кода на частотах диапазонов L1 и L2 и по сигналам стандартного кода на диапазоне L1.

Воспользуемся моделью псевдодальности в упрощенном виде.

     (3.1)

где t – номинальное время приема (системное время, время GPS или ГЛОНАСС); – ионосферная задержка; – тропосферная задержка; dtⁱ и dt_A – поправки часов спутника и приемника; – геометрическая дальность; – погрешность измерения псевдодальности, имеющая порядок одного метра и более (шум измерений псевдодальности). В левой части уравнения (3.1) находятся измеренные или известные с некоторыми погрешностями величины.

Упрощенную модель фазовых измерений можно представить в виде выражения.

   (3.2)

Здесь – погрешность измерения фазы или шум измерений. Он имеет порядок 1 – 2 мм, откуда видно, что фазовые измерения значительно точнее кодовых, .

С использованием фазовых измерений измеренная спутниковым приемником в момент первого наблюдения фаза равна разности между фазой принятого от спутника сигнала несущей волны и сигнала, созданного в приемнике. Когда сигнал спутника принимается, может измеряться только дробная часть фазы, то есть целое число волн , называемое начальной неоднозначностью фазы, неизвестно. При последующих наблюдениях приемником дополнительно фиксируется число целых циклов частоты, накопленных от начального наблюдения. Фазу в циклах выражают в единицах расстояния умножением на длину волны.

Уравнения (3.1), (3.2) как математические модели определяют связь псевдодальностей, которые можно получить непосредственно, с истинной геометрической дальностью. Их соотношение определяется прежде всего поправочными элементами погрешностей. И если будет известно их значение вместе с измеренной псевдодальностью, то задача определения самой геометрической дальности будет решена. Совокупность геометрических дальностей можно использовать для решения пространственной засечки. В этом заключается прямое решение задачи местоопределения наземного пункта. Однако такой подход приемлем в том, случае, если в наличии имеются необходимые измерения. Это даст однозначное значение местоопределения, но с соответствующей точностью, которая не сможет удовлетворить подавляющую массу потребностей. Поэтому необходимо использовать как можно больше избыточных измерений, что влечет за собой извлечение окончательного результата с вероятностных позиций.

Но обязательным условием данного решения является наличие математического аппарата на решение этой задачи. Как правило, подобный аппарат реализуется путем линеаризации уравнений (3.1) и (3.2), что и было достигнуто в предыдущем параграфе.

Далее так же как и в предыдущем параграфе для обобщенной модели приведем необходимые выкладки решения задачи.

Для кодовых измерений (абсолютные местоопределения) будет справедливо выражение, которое уже получено выше (3.1)

Здесь геометрическая дальность это та же исходная функция, которая линеализируется и рассмотрена выше. По ней составлена система уравнений поправок (3.2.4).

Напомним, эти уравнения как и в параметрическом способе имеют следующий вид:

, в котором

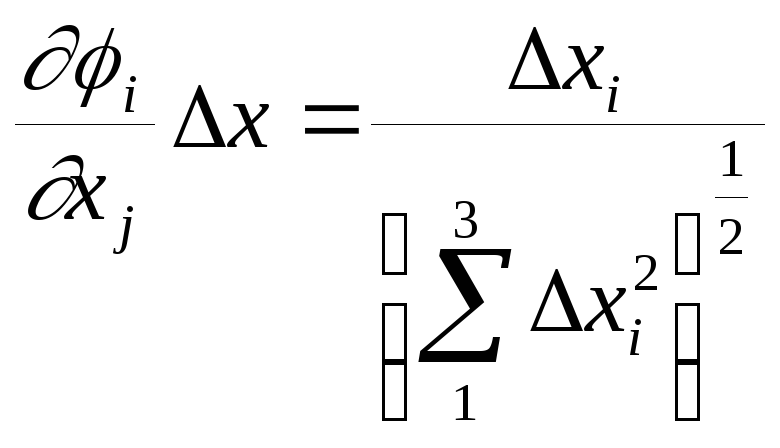соответсвуют выражению (3.2.3)

Представим (3.1) в ином виде,- в виде выражения связи псевдодальности с геометрической дальностью:

(3а)

Геометрическую дальность линеализируем разложением в ряд Тейлора и подставляем обратно в (3а).

(3.8)

или

где - сумма производных, которые еще называются направляющими косинусами, - свободный член уравнения поправки (3.8) как разность между известным значением геометрической дальности и псевдодальности.

После введения дополнительных обозначений данное уравнение можно представить короче:

(3в)

где - суммарная поправка за искажения атмосферы и часов, определяемая по модельным данным и часам.

Для множества измерений составляется система уравнений (3.в)

и так же как задача предыдущего параграфа решается по методу наименьших квадратов параметрическим способом с тем отличием, что здесь в системе присутствуют дополнительные элементы, присущие практическим задачам.

Для фазовых измерений:

     (3.9)

Таким образом, одновременные наблюдения не менее, чем четырех спутников GPS (рис. 3), позволяют определить и координаты пункта и время. Описанный метод определений координат называется абсолютным методом. Точность этого метода обычно невысокая и составляет в среднем 50 -100 м. 

В дифференциальном методе одно и то же созвездие спутников наблюдают не менее двух приемников (рис. 4). Один из них, базовый, находится в точке с известными истинными координатами  и непрерывно определяет свои координаты по псевдодальностям. Разность истинных и измеренных координат базового приемника дает значение дифференциальной поправки:

 

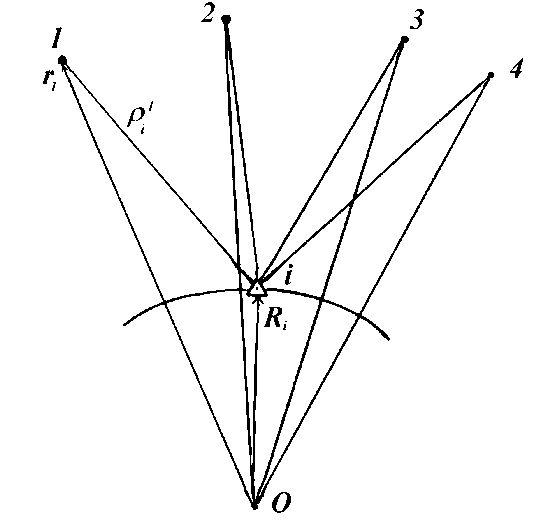
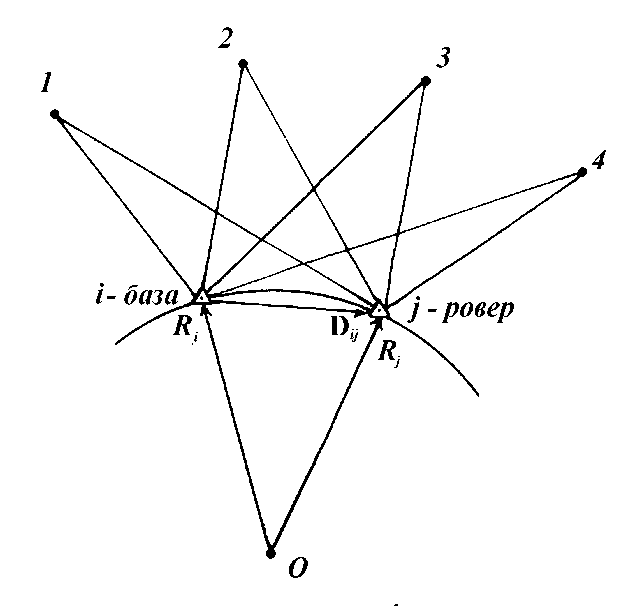
Рис. 3. Абсолютный метод Рис. 4. Дифференциальный метод . (33) Полевой приемник (ровер) находит свои координаты по тем же спутникам и, используя дифференциальную поправку, исправляет их: . (34) Точность измерений будет тем выше, чем сильнее будут коррелированы ошибки измерений. В фазовых геодезических приемниках измеряется не только псевдодальность, но и разность фаз на частоте несущей между принятым сигналом и сигналом, созданным в приемнике. Точность фазовых измерений значительно выше, чем кодовых, относительная ошибка стороны обычно получается на уровне 10^-6 и меньше.