Интегралы орбитального движения

При решении практических задач, связанных с использованием ИСЗ, требуется знать положение спутника в пространстве в произвольный момент времени. Для этого, из решения 3х дифференциальных уравнений второго порядка, необходимо найти x,y,z-искомые координаты спутника, которые выражаются функциями от независимого переменного t и 6ти произвольных постоянных (параметров орбиты).

В связи с этим, рассмотрим движение спутника по эллиптической орбите, т.е. установим 6 параметров, из которых 5 определяют пространственное положение орбиты, а 6ой определяет мгновенное положение ИСЗ в пространстве и является функцией времени.

Для этого построим эллиптическую орбиту так, чтобы один из фокусов эллипса совпадал с точкой О (центр масс Земли). Рассмотрим движение спутника с массой вокруг Земли. Землю будем считать точечной массой или шаром с массой со сферически симметричным распределением плотности. В таком гравитационном поле отвесные линии являются прямыми, направленными к центру сферы. Массу спутника будем считать ничтожно малой по сравнению с массой Земли. В дополнении к этим условиям, будем также считать, что на движение спутника не влияют никакие другие силы, кроме притяжения Земли. При таких условиях задача о движении спутника в небесной механике называется ограниченной задачей двух тел.

Начало инерциальной системы координат поместим в геоцентр . В этой системе положение спутника будем задавать его радиусом-вектором , скорость – вектором , а ускорение – вектором а:

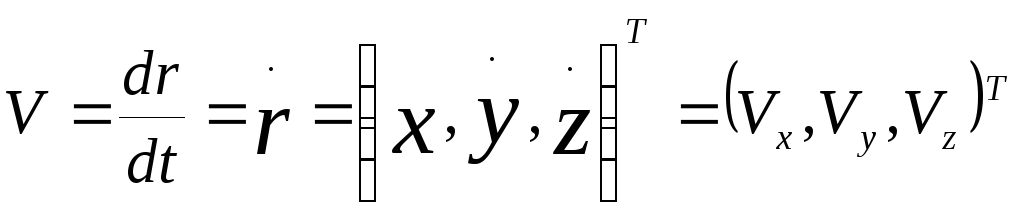
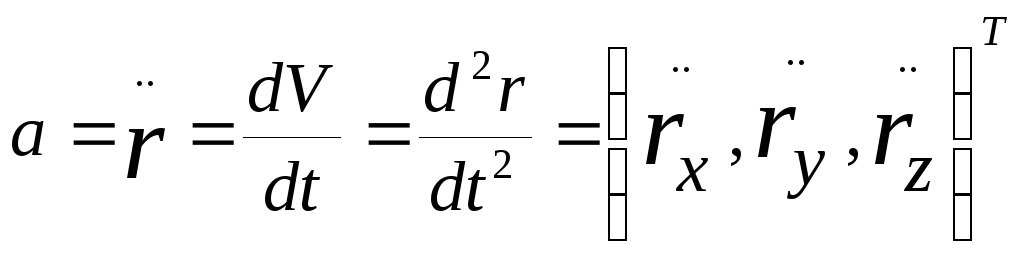
Точками над символами обозначается дифференцирование по времени, то есть одна точка – производная первого порядка, две точки – производная второго порядка и т. д.

Центральное гравитационное поле Земли характеризуется потенциалом

Вызывающее в движении спутника ускорение, равное по абсолютной величине

где геоцентрическая гравитационная постоянная, а расстояние спутника от геоцентра. Вектор ускорения , который, как и вектор силы , направлен по радиусу-вектору к центру масс Земли, получаем путём умножения на единичный вектор , то есть

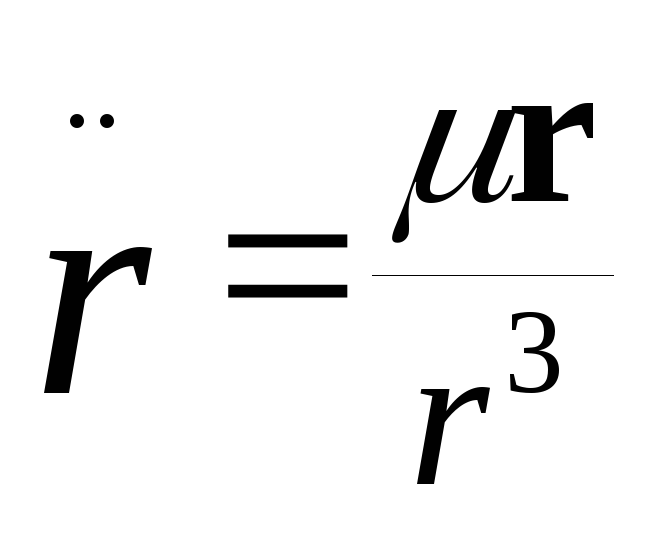
Полученное дифференциальное уравнение описывает невозмущённое, или Кеплерово, движение. Это уравнение в координатной форме записывается в виде системы обыкновенных дифференциальных уравнений 2-го порядка:

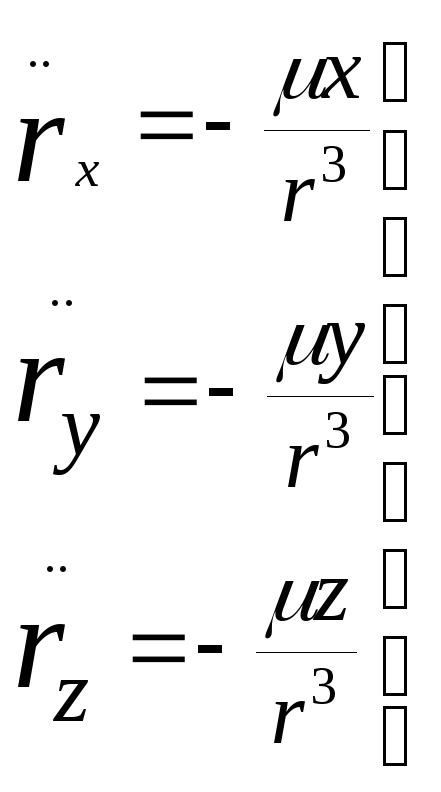
Данные уравнения должны иметь шесть независимых постоянных интегрирования, которые позволяли бы вычислять на любой момент положение и скорости спутника.

Первые интегралы определяющие закономерности невозмущённого движения.

1. Векторный интеграл площадей:

–

Орбита в пространстве

Орбита в плоскости орбиты

Постоянный вектор С является вектором кинетического момента спутника, направленным по нормали к плоскости отбиты, а его компоненты являются проекциями кинетического момента на координатные оси. Вектор С задаёт ориентировку плоскости орбиты в пространстве. Орбитальное движение происходит в плоскости, проходящей через центр, а сама отбита является плоской кривой.

2. Интеграл энергии:

где постоянная энергии. Умножение уравнения на даёт:

откуда видно, что полная энергия равная сумме кинетической и потенциальной энергий остаётся постоянной.

3. Векторный интеграл Лапласа:

Постоянный вектор называется вектором Лапласа. Он находится в плоскости орбиты и направлен в ближайшую к центральному телу точку орбиты спутника , называемую перигеем. Противоположная ему, наиболее удалённая от геоцентра точка орбиты, называется апогеем , а соединяющая их линия называется линией аспид. Линия, по которой пересекаются плоскости экватора и орбиты, называется линией узлов. В восходящем узле спутник пересекает плоскость экватора, переходя из южного полушария небесной сферы в северное. В нисходящем узле спутник переходит из северного полушария в южное.

Первые интегралы связаны соотношениями: