Аналитические решения спутниковых наблюдений с использованием математической модели Обобщенная математическая модель задачи пространственного определения спутниковыми методами
Решение любой задачи требует ее постановки и в первую очередь модели самой задачи. В качестве такой модели можно использовать некоторую функцию, которая представляла бы связь измеренных, т.е известных величин с неизвестными.
При
обработке геодезических измерений
используют коррелатный и параметрический
методы. В GPS
используют параметрический метод. При
этом подходе прежде всего необходимо
составить уравнение, связывающее
измеряемую величину с определяемыми
параметрами. В спутниковой геодезии
измеряемые величины и определяемые
параметры связаны основным соотношением,
иллюстрируемым рисунком.
Будучи записанным в векторном виде, это соотношение имеет вид :
В этом выражении R - геоцентрический вектор пункта Р; ρ - топоцентрический вектор спутника S; r - геоцентрический вектор спутника. Геоцентрический вектор спутника получают из его эфемерид. Геоцентрический вектор пункта является тем, что необходимо получить, работая в навигационном режиме. При выполнении геодезических измерений получают разность геоцентрических векторов пунктов. Будучи по геометрической сути системой дальномерной, GPS позволяет из измерений получать длину вектора ρ, то есть его модуль r. Уравнение (4) принимает вид
(2.3)
Именно это соотношение используют при обработке результатов измерений. Для этого его выражают в координатной форме, линеаризуют и выполняют все остальные процедуры, предусмотренные совершенным механизмом способа наименьших квадратов. Спутниковые измерения имеют много общего с другими геодезическими методами. Есть, однако, и особенности. Проявляются они на этапе постобработки и при разрешении многозначности фазовых измерений.
Рассмотрим, каким образом можно определить точное местоположение пункта наблюдения с использованием уравнения (2.3)
В качестве исходной функции согласно теории параметрического способа примем геометрическую дальность. Геометрическая дальность (2.3) представляет собой истинное расстояние между спутником и приемником. Подлежащие определению координаты пункта скрыты в геометрической дальности, которую можно явно записать как
,
(3.2)
где
–
компоненты вектора геоцентрического
положения спутника в эпоху t; XА,
YА,
ZА
– три неизвестных координаты пункта
наблюдений, образующих вектор RА
в земной геоцентрической системе.
Практическая реализация уравнения (2.3) чаще всего связывается с линеаризацией уравнения (3.2).
Выполним линеаризацию данной функции с составлением уравнения поправок вида (4.5.4).
Линеаризация функции геометрической дальности
Для удобства дифференцирования в целях линеаризации представим (3.2) в следующем виде.
,
где (3.2.1)
-
вектор квадратов разностей координат
пункта наблюдения А и спутника i.
Здесь функция представлена как степенная
сложная. Это нам скоро пригодится.
Далее согласно формуле Тейлора
выполняем
дифференцирование (3.2.1)
Данная функции является сложной степенной. Поэтому используем для этого правило дифференцирования степенной и сложной функции. Напомним, что производная степенной функции равна
,
а производная сложной функции
(3.2.2)
т.е. в нашем случае
С
учетом всего этого
,
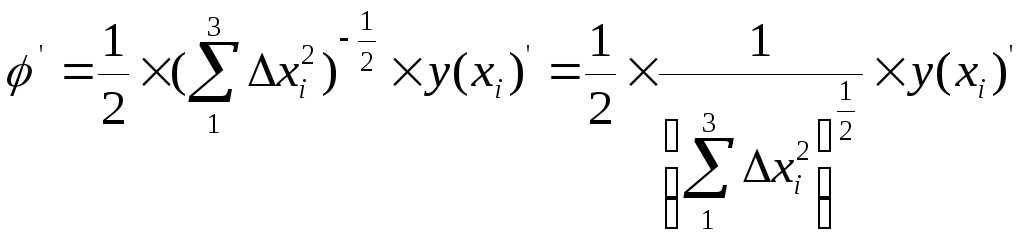а
Подставляем полученные выражения для производных в (3.2.2)
(3.2.3)
Последнее
выражение – результат линеаризации
исходной функции независимых параметров
(3.2) в виде первой производной функции
по i-му
аргументу. При этом
–
разности координат пункта и спутника.
На словах это звучит так: поправка к величине определяемого параметра равна сумме произведений первых производных исходной функции по всем ее аргументам на поправку параметра в сумме со свободным членом уравнения поправки.
На
текущий момент нами определены производные
функции по ее аргументам. Далее необходимо
определиться с поправками к координатам
наземного пункта. Обозначим этот вектор
поправок как
.
Так же нужно определить свободный член
получающихся в результате линеаризации
разложением исходной функции в ряд
Тейлора уравнений поправок, так же как
в обосновании параметрического способа.
Как они могут быть представлены?
-
это вектор поправок в координаты
определяемого пункта
=
,
но пока только по одному измерению,
соответственно по одному уравнению.
А
- не что иное, как различие между измеренной
и вычисленной величиной самого вектора
геометрической дальности. Измеренную
дальность еще называют псевдодальностью
с обозначением
как дальность предварительного
приближенного определения местоположения
пункта А относительно i-го
местоположения к-го спутника.
Иными
словами
.
Последние обозначения соответствуют i-му наблюдению либо j-го спутника, либо j-го спутника в момент времени t. Это значит, что в обработке наблюдений могут участвовать как наблюдения разных спутников, так и одного спутника в разные моменты.
Дальше можно приступать к составлению необходимой для решения задачи пространственного определения местоположения системы уравнений поправок.
Для случая наблюдения совокупности n спутников совокупность уравнений поправок можно представить в следующей матричной форме, как это представляется в параметрическом способе.
(3.2.4)
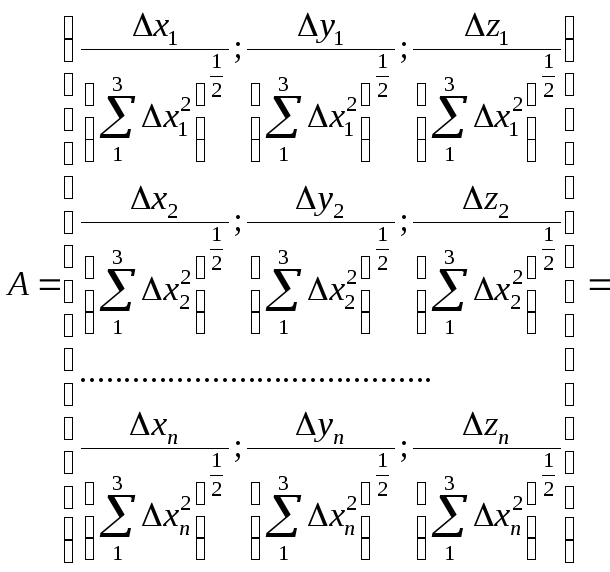
, где элементы матрицы А составляются согласно (3.2.3).
,
элементы которой в числителях представлены разностями координат между пунктом наблюдения А и i-м спутником в текущий момент времени (эпоху). А в знаменателях
=
-
это геометрическая дальность до спутника.
В
целом же элементы матрицы А вида
в разных источниках
обозначаются по-разному, но везде
называются направляющими косинусами
вектора между наземным пунктом и
спутником.
V
- вектор поправок, образующийся в
результате не достаточно точного знания
приближенного вектора дальности
в сравнении с геометрической дальностью
.
Задача (3.2.4) решается по методу наименьших квадратов параметрическим способом.
Из системы (3.2.4) составляется система нормальных уравнений
, (2.10)
решение данной системы приводит к определению вектора неизвестных
(2.11)
При
этом
,
,
где
Р – матрица весов измерений.
В литературе геометрические дальности рассматриваются как истинные значения. С ними сопоставляются и исправляются якобы измеренные величины в виде псевдодальностей. В действительности это достаточно условное разделение измеренной и истинной величины. Дело в том, что геометрическая дальность образуется в результате использования тех координат станции, которые на текущий этап обработки получены по тем же псевдодальностям. Иными словами эти величины и, в частности их ошибки, коррелированны.
Как быть? Где истина? А истина в случае абсолютных определений, - в приближениях. Каждое уточненное значение псевдодальности на очередном шаге определения местоположения можно принимать за геометрическую дальность, а измеренную дальность – за псевдодальность.
Важно заметить, что не так это нужно рассматривать в случае относительных измерений в силу того, что точно известны координаты базовой станции. По ее координатам всегда можно относительно, но точно определить координаты определяемой станции, из чего следует, что геометрическая дальность является и для нее величиной детерминированной через точные координаты базовой станции с добавлением к ним своих, грубых, но одинаково ошибочных псевдодальностей.
Далее, сейчас, когда основная операция лианиризации завершена, можно позволить себе дополнить систему уравнений и учетом дополнительных величин и введением дополнительных неизвестных, в том числе и учетом неточности знания всех поправок за искажения внешней среды и часов. Это один вариант, естественно соответствующий текущему изложению.
Можно использовать другой вариант. Составить уравнение псевдодальности со всеми необходимыми для удовлетворительного местоопределения поправками. Далее лианизировать в данном уравнении ту его часть, которая представляет псевдодальность и подставить лианизированный результат обратно в уравнение.
Необходимая совокупность уравнений системы (3.2.4)справедлива для случая детерминированных, т.е. однозначно определяемых величин. Это означает, что в системе уравнений входит необходимое число уравнений, равное числу определяемых неизвестных.
Действительно же практикуется избыточное число измерений, предполагающее избыточность числа уравнений. Из этого следует, что совокупность уравнений поправок имеет избыточную численность с вектором поправок, что порождает задачу решения избыточного числа уравнений по методу наименьших квадратов.