Вопрос № 24. Определение операции умножения матриц. Примеры. Свойства умножения. Перестановочные матрицы. Примеры.

Умножение 2-х матриц: умножение А на В возможно тогда и только тогда, когда число столбцов А равно числу строк В; произведением матрицы А размера mxk на матрицу В размера kxn называется матрица С размера mxn, каждый элемент которой равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы

Пр.: А∙В =

С11=1*0+2*1+(-3)*(-2)= 8

С12= 1*6+2*(-1)+(-3)*4= -8

С21=0*0+4*1+7*(-2)= -10

С22= 0*6+ 4*(-1)+7*4= 24

Св-ва умножения матриц:

1. АВ≠ВА

2. А(ВС)=(АВ)С

3. А(В+С)=АВ+АС

В тех случаях, когда АВ=ВА, то говорят, что матрицы А и В перестановочные (они коммутируют).

Пр.: АВ =

ВА =

-1≠3⇒ АВ≠ВА

№25 Системы двух линейных ур-ий с двумя неизв. Имеют вид:      ax+by=c       dx=ey=f где a,b,c,d,e,f-заданные числа,x,y-неизвестные.Числа a,a,d,e-коэффициенты при неизвестных;с,f-свободые члены.Решение этой системы может быть найдено двумя основными методами(подстановка,сложение /вычетание) Определители второго порядка,соотв. Данной матрице,наз.число,обознач. символом            |a11     a12| detA= |             |            |a21      a22| и определяемое рав-вом detA=a11a22-a12a21 Диагональ,образ. эл-тами  a11  и  a12,наз. главной Диагональ,образ. эл-тами  a12   a21 ,наз. Побочной

Теорема. (Правило Крамера)

            Теорема. Система из n уравнений с n неизвестными

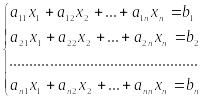
в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:

 

x_i = _i/, где

 = det A,  а _i – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов b_i.

_i =

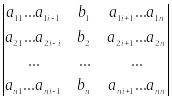
     Пример.

 

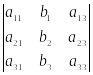A = ;   ₁= ;  ₂= ;   ₃= ;

 

x₁ = ₁/detA;       x₂ = ₂/detA;        x₃ = ₃/detA;

№26 Определители третьего порядка наз. число квадратной матрицы третьего порядка,обозн. cимволом       |a11  a 12  a 13 | A= |a21  a 22  a23 |       |a31  a32   a 33| и определяемое рав-вом detA=a11a22a33+a12a23a31+a13a21a32-a31a22a13-a21a12a33-a11a32a23 Диагональ,образ. эл-тами а11,а22,а33,наз. главной Диагональ,образ. эл-тами а31,а22 и а13,наз. Побочной

Теорема (разложение определителя по строке или столбцу).

Определитель равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения. Иначе говоря, имеет место разложение d по элементам i-й строки

d = a_{i 1} A_{i 1} + a_{i 2} A_{i 2} +... + a_{i n} A_{i n}   (i = )

или j- го столбца

d = a_{1 j} A_{1 j} + a_{2 j} A_{2 j} +... + a_{n j} A_{n j}    (j = ).

В частности, если все элементы строки (или столбца), кроме одного, равны нулю, то определитель равен этому элементу, умноженному на его алгебраическое дополнение.

Билет №27. Перестановки чисел 1,2,3,..., n. Инверсии. Подсчёт числа инверсий и четность-нечетность перестановки. Определители произвольного порядка.

Перестановка – упорядоченный набор чисел 1,2..n, трактуемый как биекция на множестве {1,2,…n}, в котором числу 1 ставят в соответствии i-тый элемент из набора N – порядок перестановки.

Перестановка является четной, если число инверсий четно. Нечетной, если число инверсий нечетно.

Инверсией в перестановке π порядка n называется всякая пара индексов i,j такая, что и π(i) > π(j). Чётность числа инверсий в перестановке определяет чётность перестановки.

Билет №28. Обратная матрица(определение, единственность ).Необходимое и достаточное условие её существования (с доказательством).

Матрица B называется обратной матрицей для квадратной матрицы A, если АВ=ВА=Е (Обратная матрицы для матрицы А обозначается A^-1 .) Если определитель матрицы равен нулю, то обратная к ней не существует. Если обратная матрица существует, то она единственна.)

Обратная матрица существует тогда и только тогда, когда определитель матрицы А не равен нулю.

(A^-1 ) ↔ (detA≠0)

Det(AB)=detA∙detB

detE=det(A∙ A^-1 )=det A^-1 ∙detA=1 → detA≠0

Билет №29. Матричная запись системы линейных уравнений. Решение систем n линейных уравнений с n неизвестными при помощи обратной матрицы.

Системой m линейных уравнений с n неизвестными называется системой вида.

Где аij коэффициент при xj

Х1, х2…хn – неизвестные

B1, b2…bm – свободные члены

можно представить в матричном виде

Х – вектор неизвестных, В – вектор свободных членов

и тогда всю систему можно записать так:

AX = B,

где A имеет смысл таблицы коэффициентов a_ij системы уравнений.

Если m = n и матрица A невырожденная, то решение этого уравнения состоит в нахождении обратной матрицы A ^{- 1}, поскольку умножив обе части уравнения на эту матрицу слева

A ^{- 1}AX = A ^{- 1}B

A ^{− 1}A — превращается в E (единичную матрицу). И это даёт возможность получить столбец корней уравнений

X = A ^{- 1}B.

Билет №30. Теорема Крамера для систем n линейных уравнений с n неизвестными (доказательство для п=3).

Если определитель отличен от нуля, следовательно, можно применить правило Крамера:

Если определитель матрицы не равен нулю, то система имеет решение и притом единственное. Это решение задается формулой: