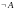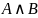Вопрос № 1. Высказывания (определение высказывания и примеры высказываний). Операции над высказываниями (определения операций отрицания , конъюнкции , дизъюнкции 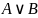, примеры составных высказываний, содержащих эти операции).

Высказывание – повествовательное предложение, о к-ом можно говорить истинно оно или ложно. (пр. три – целое число).

Отрицание – отрицанием высказывания А наз.высказывание, принимающее значение 1, если А=0, 0, если А=1. Обозн-ся (¬А) , (пр. А – 1ый экзамен сдан; (¬А) – 1ый экзамен не сдан)

Конъюнкцией высказываний А и В называется высказывание, принимающее значение 1, если А=В=1 и 0 во всех остальных случаях – бинарная операция. Обозн-ся . (А – 1ый экз сдан, В – 2ой экз сдан,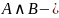 сданы оба экза).

Дизъюнкцией называется высказывание, принимающее значение 0, если А=В=0 , 1 во всех остальных случаях. Обозн-ся . (А – 1ый экзамен сдан, В – 2ой экзамен сдан, - сдан хотя бы 1 экз.)

Вопрос № 2. Высказывания. Определение операций импликации и эквивалентности. Свойства логических операций

Импликация (следствие) – истинна всегда, кроме случая, когда из истины следует ложь (1→0)

Эквивалентность (равносильность ↔) – истинно когда оба либо 0, либо 1.

Св-ва логических операций:

1. ¬(¬А)↔А

2. (АvВ)↔(ВvА)

3. (АvВ)vС↔Аv(ВvС)

4. (А^В)↔(В^А)

5. (А^В)^С↔А^(В^С)

6. ¬(АvВ)↔(¬Аv¬В)

7. ¬(А^В)↔(¬А^¬В)

8. (А→В)↔(¬В→¬А)

9. (В→А)↔(¬А→¬В)

10. ((А→В)^(В→С))→(А→С)

11. ((А↔В)v(В↔С))→(А↔С)

Вопрос № 3. Высказывания, зависящие от параметра (предикаты). Примеры. Высказывания, содержащие кванторы общности 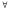и существования . Примеры таких высказываний. Отрицание высказываний, содержащих кванторы (формальная конструкция и её смысл).

Предикат – это то, что утверждается или отрицается о субъекте суждения.

Пр.: пусть Х›5

А(Х): Х›5

А(1): 1›5 – ложь, 8›5 – истина

Кванторы – логические символы, к-ые обозначают операции, ограничивающие мн-во истинности предиката.

Кв-р общности(∀) – каждый, любой, всякий

Кв-р существования(∃) – сущ-ет по крайней мере один

Правила отрицания кванторов

¬(∀ х ) = ( ∃х ) ¬Р(х)

¬(∃х) Р(х) = (∀х) ¬Р(х)

Примеры высказываний с кванторами:

1. х –одноклассник (Х – весь класс)

А(х): х поступили в ВУЗ

∃(х): А(х) – найдётся хотя бы один однокл, к-ый поступил в ВУЗ

2. А(Х), х∊Х(х∊ множ-ву параметров),∀х: А(х) (Для каждого х из Х выск.А(х)-истинно)

Отрицание высказываний с кванторами:

¬∀⇒∃; ¬∃⇒∀;

Пр.: В: (∀х: А(х)); ¬В: (∃Х:¬АХ)

Вопрос № 4. Понятие множества (по Кантору), символ принадлежности , пустое множество. Способы задания множеств. Примеры множеств, заданных различными способами. Равенство множеств, определение подмножества, символ включения , понятие несобственного подмножества. Примеры.

Множество (по Кантору) – многое, мыслимое как единое.

Элементы мн-ва – объекты, составляющие это мн-во.

Способы задания мн-в

1. Перечислением своих элементов: А=[a, b, c,…]

2. Через описание ограничительного св-ва. А=[х| Р(х)]- А мн-во таких элементов х, к-ые обладают св-ом Р(х).

Принадлежность(∊) – элем-т х явл. эл-ом мн-ва А

Пустое мн-во(∅) – мн-во, не содержащее ни одного эл-та.

Равенство мн-в – мн-ва А и В равны, если они состоят из одних и тех же эл-тов.

Подмн-во – подмн-во В наз.подмн-ом А, если все эл-ты мн-ва В принадлежат мн-ву А.

Включение (⊂) – если каждый эл-т х мн-ва Х явл.эл-ом мн-ва У, то говорят, что мн-во Х содержится во мн-ве У.

Несобственное подмн-во – когда непустое подмн-во В совпадает с мн-ом А.

Вопрос № 5. Определения операций над множествами (объединение 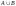, пересечение 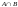, разность 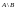). Понятие универсального множества, операция дополнения .

Иллюстрация операций с помощью диаграмм Венна. Примеры.

Объединение (А∪В) – все элементы мн-ва А и все эл-ты мн-ва В, вместе взятые составляют новое мн-во.

Пересечение (А∩В) – так называются два мн-ва, эл-ты к-ых принадлежат как мн-ву А так и мн-ву В.

Разность (А\В) – мн-во, сост.из всех эл-ов А, не принадл.мн-ву В

Универсальное мн-во – содержащее все мыслимые объекты. Всякое мн-во рассматривают как часть большого мн-ва, например, треугольники, квадраты, окружности, можно считать подмн-ами плоскости, целые числа – подмн-ами действит.чисел.

Дополнение – мн-во всех тех эл-ов из УМ, к-ые не принадл.ему. (Если В – подмн-во А, то разность А и В также называют дополнением мн-ва).

Вопрос № 6. Определение эквивалентности множеств. Мощность множества. Примеры множеств, имеющих одинаковую мощность. Связь понятий равенства и эквивалентности. Множество натуральных чисел (аксиомы Пеано). Определение конечного множества. Объединение конечных множеств.

Эквивалентность мн-в – если между мн-ами А и В установлено взаимнооднозначное соответствие/каждому эл-ту мн-ва А сопоставлен один и только один эл-т мн-ва В и наоборот/

Объединение конечного (счётного) мн-ва счётных мн-в счётно.

Мощность мн-ва – это обобщение понятия количества (числа) эл-ов мн-ва, к-ое имеет смысл для всех мн-в, включая бесконечные.

Пр.: мн-во чётных целых чисел Е имеет такую же мощнсть, что и мн-во целых чисел Z. Определим так:

P: E→Z так P (X)= X/2 – биекция, поэтому |Z|=|E|.

Если мн-ва равны, то они эквивалентны, а если мн-ва эквив., то это незначит, что они равны.

Аксиомы Пеано:

1. 1 есть натуральное число;

2. Следующее за натур.ч-лом есть натур.ч-ло;

3. 1 не следует ни за каким натур.ч-лом;

4. Всякое натур.ч-ло следует только за одним натур.ч-лом;

5. Аксиома полной матем.индукции: если нек.высказывание истинно для n=1 и если из того, что оно верно для n следует, что оно верно для n+1, то оно верно для любого натурального х

Конечное мн-во – мн-во, состоящее из конечного числа эл-ов./ говорят, что мн-во А конечно, если оно эквивалентно нек.отрезку натур.ряда/

Мощность конечного м-ва совпадает с ч-лом его эл-ов

Объединение конечного мн-ва – счётно.

Вопрос № 7. Бесконечные множества. Счетные множества. Примеры счетных множеств.

Объединение счетных множеств. Необходимое и достаточное условие бесконечности множества (с доказательством).

Бесконечное мн-во – мн-во, не явл-ся конечным. Пр.: мн-во натур.чисел.

Св-ва:

1. Всякое подмн-во бесконечного мн-ва конечно или счётно;

2. Сумма любого конечного или счётного мн-в есть счётное мн-во

3. Всякое бесконечное мн-во содержит счётное подмн-во.

Счётное мн-во – эквивалентное натуральному ряду. Это такое бескоенчное мн-во, элементы к-го можно «пронумеровать» при помощи мн-ва натур.чисел, при к-ом каждый эл-т мн-ва получит свой единств.номер.

Пр.: мн-во всех натуральных/ рациональных чисел.

Св-ва объединений счётных мн-в:

1. Объедин.2-ух счётных мн-в – счётно;

2. Объедин.счётного числа счётных мн-в – счётно.

Необходимое и достаточное условие бесконечности мн-ва (теорема): всякое мн-во бесконечно тогда и только тогда, когда оно эквивалентно некоторому своему подмн-ву; (≠∅).

(А – беск.)⟷ (∃В : В≠А; В≠∅; В⊂ А; В∼А)

Док-во теоремы: рассм.мн-во А

⊐А – бесконечно. Докажем, что оно эквив.нек.своему истинному подмн-ву;

∃В: {b1, b2, … ,bn, bn+1}; В⊂А

По лемме у мн-ва А сущ.счётное подмн-во. Счётное подмн-во разобьём на 2

В1 {b1; b3; b5; …; bn+1;…}

B2 {b2; b4; b6; …; b2n;…}

B=B1∪B2, B1∩B2=∅

Очев.,что В1∼В2=В

Представим мн-во А след. сп-бом: А= В∪(А\В)

Рассм.мн-во А\В2; А\В2=В1∪(А\В)

Докажем, что ( А\В2) ∼А

А=В∪(А\В); А\В2=В∪(А\В)

Очев,что (А\В)∼(А\В)

}⇒ А∼(А\В2)

В∼В1

Заметим, что мн-во (А\В2) – беск., как объединение счётного мн-ва В1 с мн-ом (А\В).

ч.т.д.

Вопрос №8. Понятие иррационального числа. Доказательство иррациональности 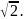Множество вещественных (действительных) чисел Несчетность множества вещественных чисел из интервала (0;1)(с доказательством). Континуальные множества. Примеры.

Иррациональное число-вещественное число,кот. не явл. рациональным,т.е кот. не может быть представлено в виде дроби m/n, где m-целое число, n-натуральное число

Док-во того,что √2 -иррацианальное число

Цель Евклида состояла в доказательстве того, что число √2 не представимо в виде дроби. Поскольку Евклид использовал доказательство от противного, первый шаг состоял в предположении, что верно противоположное утверждение, т.е. что число √2 представимо в виде некоторой неизвестной дроби. Запишем эту дробь в виде p/q, где p и q — два целых числа.

Прежде чем приступать к самому доказательству, необходимо напомнить некоторые основные свойства дробей и четных чисел.

1) Если взять любое число и умножить его на 2, то произведение должно быть четным. По существу, это определение четного числа.

2) Если квадрат некоторого числа четен, то и само число должно быть четным.

3) Наконец, дроби можно сокращать: 16/24 это то же самое число, что и 8/12. Чтобы убедиться в этом разделите числитель и знаменатель дроби 16/24 на общий множитель 2. Кроме того, число 8/12 это же самое, что и 4/6, а 4/6 это же самое, что и 2/3. Дробь 2/3 не подлежит дальнейшему сокращению, так как 2 и 3 не имеют общих множителей. Дробь невозможно сокращать до бесконечности.

Помнению Евклида число √2 не представимо в виде дроби. Но поскольку Евклид использовал доказательство от противного, он начал с предположения, что дробь p/q, равная числу √2, существует, а затем исследовал, к каким последствиям приводит такое предположение:√2 = p/q.

Возводя обе части равенства в квадрат, получаем:2 = p²/q.²

После несложного преобразования запишем это равенство в виде:2q²= p².

Из 1) мы знаем, что число p² должно быть четным. Кроме того, из 2) нам известно, что число p также должно быть четным. Но если p четно, то, как следует из 1), его можно записать в виде 2m, где m — некоторое другое целое число. Подставляя p = 2m в равенство для p², получаем:2q ²= (2m)² = 4m².

Сокращаем правую и левую части равенства на 2:q² = 2m.²

Число q² должно быть четным. Значит, и само число q должно быть четным. Но если это так, то q можно записать в виде q = 2n, где n — некоторое другое целое число. Возвращаясь к исходной записи числа √2, получаем:√2 = p/q = 2m/2n.

Дробь 2m/2n можно сократить, разделив числитель и знаменатель на 2:√2 = m/n.

Мы получаем дробь m/n, которая проще, чем p/q (имеет меньший числитель и знаменатель). Теперь мы как бы снова оказались находимся на исходной позиции, и, проделав с дробью m/n все, что мы проделали с дробью p/qn, получим в результате еще более простую дробь, например, g/h. Проделав с этой дробью тоже самое, приведем ее к еще более простой дроби t/f, и т.д. Аналогичную процедуру можно проделывать бесконечное число раз. Но из 3) мы знаем, что дробь невозможно упрощать бесконечно — всегда существует простейшая дробь. Но наша исходная гипотетическая дробь p/q, насколько можно судить, не подчиняется этому правилу. Следовательно мы получили противоречие. Итак, мы можем утверждать, что число √2 не представимо в виде дроби, а это означает оно является иррациональным числом.

Мн-во вещественных чисел-является бесконечным, состоит из рациональных и иррациональных чисел.Рациональные-десятичные, периодические дроби, представленные в виде p/q,q>0,p и q-целые числа.Иррациональные-десятичные непериодические дроби,например,√2,³√5 и тд.

Континуальное мн-во- мн-во эквивалентное мн-ву всех действит. чисел, заключ. между 0 и 1.

Вопрос №9. Определение бинарного отношения на множестве. Отношение эквивалентности. Примеры эквивалентностей. Связь отношения эквивалентности и разбиения множества на классы (теорема с доказательством).

Бинарное отношение эл-тов на мн-ве-мн-во упорядоченных пар эл-тов.

Отношение эквивалентности(~)-это бинарное отношение,для кот. Выполнены следующие условия:

1)рефлексивность: a~a для любого a в X

2)симметричность: если а~b,то b~a

3)транзитивность:если a~b и b~c ,то a~c

Например,множество пар целых чисел, которые имеют одинаковый остаток при делении на одно и то же число

Каждому отношению эквивалентности соотв. разбиение мн-ва на классы и каждому разбиению мн-ва на классы определяет соответствие.

Вопрос №10. Отношение порядка. Упорядоченность множества рациональных чисел. Упорядоченность вещественных чисел (с использованием Дедекиндова сечения).

Отношение порядка-бинарное отношение R на мн-ве X называется отношение порядка или отношение частичного порядка, если имеют место рефлексивность Vx(xRx), транзитивность VxVyVz(x||y ^y||x=>xRz), антисимметричность VxVy(xRy^yRx=>x=y)

Дедекиндово сечение(узкая щель)-один из способов построения вещественных чисел и радиональных.Введён Дедекиндом.Мн-во вещественных чисел определяется как мн-во дедекиндовых сечений.На них возможно проводить операции сложения и умножения.

Разбиение мн-ва рациональных чисел Q на два подмн-ва A и B такие,что a<b для любых aA и bB,A не имеет максимального эл-та.

Например,

вещественному числу √2 соотв. дедекиндово сечение, определяемое A={xQ|x<0;0;x²=<2} и B={xQ|x>0;x²>2}

Интуитивно можно представить,что для того,чтобы определить √2,мы рассекли мн-во на две части:все числа,что левее √2,и все числа,что правее √2 ;соотв.,√2 равен точной нижней грани мн-ва B

Вопрос №11. Определения отображения множеств. Определения образа элемента и образа множества, прообраза и полного прообраза элемента, прообраза множества. Примеры.

Отображение.Пусть даны два мн-ва X и Y. Такое соотв-ие,при кот. каждому эл-ту xX cоотв.(единственный) эл-т yY,наз. Отображение мн-ва X в мн-во Y;в частности, сели каждый эл-т yY соотв. по крайней мере одному эл-ту xX,то таоке соотв. наз. Отображением X на Y.

Если эл-т x cоотв. y,то y наз. образом эл-та,а x-прообразом эл-та y.

Записывается x->y или y=f(x).Мн-во A всех эл-тов xX, имеющих один и тот же образ y=Y,наз. полным образом эл-та y

Примеры.

1)Пусть D-мн-во действит. чисел.Соотв. x->|x| будет отображением мн-ва D в себя же и отображенеим D на мн-во неотрицат. чисел.Прообразом числа 0 будет один 0,число y>0 имеет два прообраза +y и -y

2)Поставим в соотв. каждой точке квадрата её проекцию на основание.Получим отображение квадрата на отрезок.Полным прообразом каждой точки основания юудет мн-во всех точек квадрата,лежащих на перпендикуляре к основанию,восстановленном в данной его точке.

Вопрос №12 Определения инъекции, сюръекции, биекции. Примеры отображений, обладающих (или не обладающих) указанными свойствами.

Инъекция:отображение F:X->Y наз. инъекцией(вложением,взаимно однозначным отображением в мн-во Y),если разные эл-ты мн-ва X переводятся в разные эл-ты мн-ва Y

Формально значит,что если два образа совпад.,то совпад. их прообразы(F(x)=F(y)=>x=y)

Инъективность явл. необход. усл. биективности(достаточно вместе с сюръективностью)

Примеры.

1)F:R_>0->R,F(x)=lgx-инъективно

2)F:R₊->R_+,F(x)=x²-инъективно

3)F:R->R_+,F(x)=x²-не является инъективным (F(-2)=F(2)=4)

Биекция.Ф-ция f:X->Y наз. биекцией (и обозн. F:X<->Y),если она:

1)переводит разные эл-ты мн-ва X в разные эл-ты мн-ва Y(инъективность).

Vx1X,Vx₂X(f(x₁)=f(x₂)=>x₁=x₂)

Биекцию также наз. взаимно однозначным отображением.Мн-ва,для кот. сущ. Биекция,наз. равномощными.

Примеры.

1)f(x)=x,f(x)=x³-биективные ф-ции из R в себя.Любой моном одной переменной нечётной степени явл. биекцией.

2)f(x)=e^x-биективная ф-ция в R₊=(0, +бесконечность).Но если её рассм. как ф-цию в R,то она уже не будет биективной(у нуля и отр. Чисел не будет прообразов).

3)f(x)=sin x не явл. биективной ф-цией,если считать её определённой на всём R.

Cюръекция.Отображение F:X->Y наз. сюръективным(сюръекцией,отображением на Y),если каждый эл-т мн-ва Y явл. образом хотя бы одного эл-та мн-ва X, т.е. VyYxX:y=F(x)

Для случая числовых ф-ций это выражается как «ф-ция,прин. Все возм. Знач.»

Примеры.

1)F:R->[-1;1],F(x)=sin x-сюръективно

2)F:R->R_+, F(x)=x²-сюръктивно

3)F:R->R,F(x)=x²-не явл. сюръекцией

Вопрос № 14. Определение числовой функции как частного случая отображения. Определение графика функции. Примеры функций и их графиков. Некоторые свойства (чётность-нечетность, периодичность, монотонность, ограниченность). Примеры

функций обладающих (или не обладающих) указанными свойствами.

В матем.числовая функция – это функция области, определения и значений к-ой являются подмножествами числовых множеств — как правило, множества действительных чисел или множества комплексных чисел.

Пусть дано отображение. Тогда его графиком Г называется множество.

График функции — множество точек, у которых абcциссы являются допустимыми значениями аргумента x, а ординаты — соответствующими значениями функции y.

Пр.: лин.ф-ция, У=2х+1

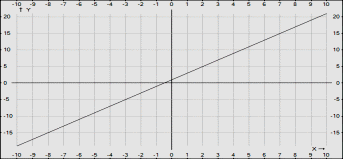
Нечётная функция — функция, меняющая знак при изменении знака независимого переменного/ функция, симметричная относительно центра координат.

Пр.: Синус .

Тангенс .

Чётная функция — это функция, не изменяющая своего значения при изменении знака независимого переменного / функция, симметричная относительно оси ординат.

Пр.: Косинус .

Периодическая функция ― функция, повторяющая свои значения через какой-то ненулевой период, то есть не меняющая своего значения при добавлении к аргументу фиксированного ненулевого числа (периода).

Пр.: Все тригонометрические функции являются периодическими.

Монотонная функция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательно, либо всегда неположительно. Если в дополнение приращение не равно нулю, то функция называется строго монотонной.

Пр.: Парабола f(x) = x² строго убывает на и строго возрастает на .

Вопрос № 15 Определение комплексного числа как упорядоченной пары вещественных

чисел. Вещественная и мнимая части комплексного числа. Мнимая единица. Комплексно-сопряженное число. Определение равенства комплексных чисел. Примеры.

Определение. Комплексным числом z называется выражение , где a и b – действительные числа, i – мнимая единица, которая определяется соотношением: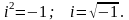 При этом число a называется вещественной частью числа z (a = Re z), а b- мнимой частью (b = Im z).Если a =Re z =0, то число z будет чисто мнимым, если b = Im z = 0, то число z будет действительным. Определение. Числа и 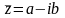называются комплексно – сопряженными.

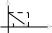A(a;b)

B

a

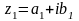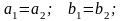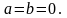Определение. Два комплексных числа и называются равными, если соответственно равны их вещественные и мнимые части: Определение. Комплексное число равно нулю, если соответственно равны нулю вещественная и мнимая части. Понятие комплексного числа имеет геометрическое истолкование. Множество комплексных чисел является расширением множества вещественных чисел за счет включения множества мнимых чисел. Комплексные числа включают в себя все множества чисел, которые изучались ранее. Так натуральные, целые, рациональные, иррациональные, вещественные числа являются, вообще говоря, частными случаями комплексных чисел. Если любое вещественное число может быть геометрически представлено в виде точки на числовой прямой, то комплексное число представляется точкой на плоскости, координатами которой будут соответственно вещественная и мнимая части комплексного числа. При этом горизонтальная ось будет являться вещественной числовой осью, а вертикальная - мнимой осью.

Таким образом, на оси ОХ располагаются вещественные числа, а на оси ОY – чисто мнимые.С помощью подобного геометрического представления можно представлять числа в так называемой тригонометрической форме.

Мнимая единица — число, квадрат которого равен отрицательной единице. Обозначается как латинская i или j. Она позволяет расширить поле действительных чисел до поля комплексных чисел.

Степени i :