Замечательные пределы
Первый замечательный предел:
Доказательство:
При
справедливы неравенства
.
Разделив
все части этого неравенства на
>
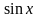0, получим
или
.
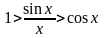Это неравенство, доказанное для любых
из интервала (0;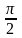
),
верно для любого
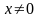из
интервала (-
;
)
в силу четности функций, входящих в это
неравенство.
А
раз
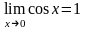и
,
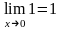то
.
Второй замечательный предел:
.
Чтобы приблизительно представить себе поведение функции при малых
приведем таблицу значений этой функции:
|
1/2 |
1/3 |
1/4 |
0.01 |
0.001 |
|
2.25 |
2.37… |
2.44… |
2.7047… |
2.7169… |
Из этой таблицы видно, что с уменьшением функция увеличивается. Оказывается, что это имеет место для всех >0, а из этого следует, что функция имеет предел.
Доказательство:
.
Рассмотрим два случая:
1.
Пусть 
.
Каждое значение x заключено между двумя
положительными целыми числами: 
,
где 
—
это целая часть x.
Отсюда следует:
,
поэтому
.
Если
,
то 
.
Поэтому, согласно пределу
,
имеем:
.
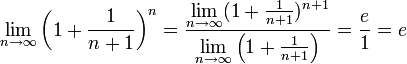
По признаку (о пределе промежуточной функции) существования пределов
.
2.
Пусть 
.
Сделаем подстановку − x = t,
тогда
.
Из
двух этих случаев вытекает, что 
для вещественного
x.
Эквивалентные функции. Символика о и о
Определение:
функция
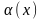называется
бесконечно
малой
при
,
если
= 0.
функция называется бесконечно большой при , если
=
.
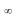Теорема (критерий эквивалентности):
Пусть
,
-бесконечно
малые функции при
.
-
.
Тогда
~
при
.
Доказательства:
(
).
Пусть
~
,
,
то есть
.
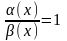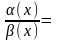
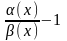=0,
то есть .
(
).
.,
.
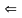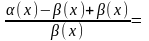
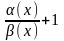=1.
Теорема (о замене на эквивалентные):
Пусть
функция
~
,
~
при
и существует
,
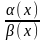тогда существует и
=
.
То есть выражение или функцию можно
заменять на эквивалентное.
=
*
*
=
.
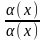Классификация разрывов
Определение: Точка а называется точкой устранимого разрыва функции y = f{x} , если предельное значение функции в этой точке существует, но в точке а функция f(x) или не определена, или ее частное значение f(a) в точке а не равно предельному значению.
Определение: Точка а называется точкой разрыва 1-ого рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу правое и левое предельные значения.
Определение: Точка а называется точкой разрыва 1-ого рода, если в этой точке функция f(x) не имеет по крайней мере одного из односторонних предельных значений или если хотя бы одно из односторонних предельных значений бесконечно.
Первая теорема Вейерштрасса
Теорема: Если функция непрерывна на сегменте, то она ограничена на нем.
Пусть
.
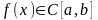Тогда
ограничена
на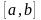
.
Доказательство:
Докажем, что
.
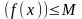Предположим
противное, то есть
.
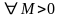
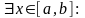
Возьмем
=1,2,3…
Получим
:
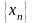1)
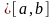
2)
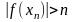
Из этих определений
получаем
.
=>
-
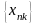подпоследовательность последовательности
:
.
-
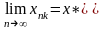непрерывна в точке
=>
.
-
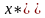подпоследовательность последовательности
:
=>
.
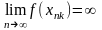Противоречие.