7. Свойства пределов, связанные с арифметическими операциями над последовательностями

Пусть 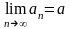, 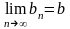. Тогда:

1) существует

2) существует

3) если 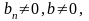то существует .

Доказательства:

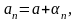
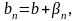где и - бесконечно малые последовательности.

1)

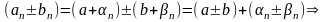
2 ) =

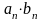бесконечно малая бесконечно малая

бесконечно малая

3) 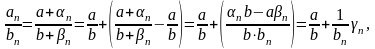где

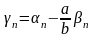- бесконечно малая последовательность.

.

8. Свойства сходящихся последовательностей: предельный переход в неравенствах

- сходящаяся : .

Любой элемент 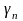сходящейся последовательности можно представить в виде:

= a + , где - элемент бесконечно малой последовательности

Теорема: Сходящаяся последовательность имеет только один предел

Доказательство: Пусть a и b – пределы сходящейся последовательности . Тогда, используя специальное представление для элементов сходящейся последовательности , получим = a + , = b +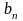 , где , - элементы бесконечно малых последовательностей. Вычитая одно из другого получим - = a – b, т.к. , - элементы бесконечно малых последовательностей => - = 0 => a = b

Теорема: Сходящаяся последовательность ограничена

Теорема: Сумма сходящихся последовательностей, есть сходящаяся последовательность, предел которой, равен сумме пределов исходных последовательностей. (то же самое с разностью и произведением и частным).

Теорема: (о предельном переходе в неравенство):

Если элементы сходящейся последовательности, начиная с некоторого номера удовлетворяют неравенству ≥ b ( ≤ b), то и предел a этой последовательности удовлетворяет неравенству a ≥ b (a ≤ b).

Доказательство: Пусть все элементы , по крайней мере начиная с некоторого номера, удовлетворяют неравенству ≥ b. Требуется доказать неравенство a ≥ b. Предположим, что a < b. Поскольку а – предел последовательности , то для положительного ε = b – a можно указать номер N такой, что при n ≥ N выполняется неравенство | - a| < b – a. Это неравенство эквивалентно следующим 2ум неравенствам: - (b – a) < - a < b – a. Используя правое из этих неравенств, мы получим < b , а это противоречит условию теоремы. Случай 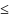b рассматривается аналогично. Теорема доказана.

9. Монотонные последовательности. Признак сходимости монотонной последовательности

Определение: -монотонно возрастающая (монотонно убывающая), если ( ). Если неравенства строгие, то последовательности строго возрастающие (убывающие).

Теорема: Если возрастающая (убывающая) последовательность ограничена сверху (снизу), то она сходится.

Доказательство: Так как последовательность { } ограничена, то множество ее элементов имеет точные верхнюю и нижнюю грани X и X’. Докажем, что если { } – возрастающая последовательность, то ее пределом будет указанная точная верхняя грань X’; если же { } – убывающая последовательность, то ее пределом будет указанная точная нижняя грань X . Мы ограничимся случаем возрастающей последовательности, поскольку для невозрастающей последовательности рассуждения аналогичны.

Поскольку X’ – точная верхняя грань множества элементов последовательности { } , то для любого ε > 0 можно указать элемент такой, что > X’ – ε и ≤ X’ (любой элемент не больше верхней грани X’, ≤ X’ ). Сопоставляя указанные неравенства получим неравенства 0 ≤ X’ - < ε . Так как { } - возрастающая последовательность, то при n ≥ N справедливы неравенства ≤ ≤ X’. Отсюда следует, что при n ≥ N выполняются неравенства 0 ≤ X’ - ≤ X’ - . Выше мы отвечали, что X’ - < ε, поэтому при n ≥ N справедливы неравенства 0 ≤ X’ - < ε, из которых вытекает неравенство

| - X’ | < ε. Таким образом, установлено что, X’ – предел последовательности { } . Теорема доказана.