18. Бесконечно малые и бесконечно большие функции. Односторонние пределы

Определение: Функция y = f(x) называется бесконечно малой в точке x = a при (x a), если

Если функция y = f(x) имеет равное b предельное значение в точке a , то функция

(x) = f(x) – b является бесконечно малой в точке a

= 0

Определение: Функция y = f(x) - бесконечно большая, при , если

Функция y = f(x) называется бесконечно большой в точке а справа (слева), если для любой сходящейся к а последовательности значений аргумента x, элементы который больше а (меньше а), соответствующая последовательность f(x₁) , f(x₂),…, f(x_n) значений функции является бесконечно большой последовательностью определенного знака

Определение: Односторонние пределы

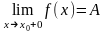, если .

, если .

19. Непрерывность функции в точке. Примеры непрерывных функций

Функция f(x) называется непрерывной в точке а, если предельное значение этой функции в точке а существует и равно частному значению f(a)

Функция f(x) называется непрерывной в точке а, если для любой сходящейся к а последовательности значений аргумента х соответствующая последовательность f(x₁) , f(x₂),…, f(x_n) значений этой функции сходится к числу f(a)

Функция f(x) называется непрерывной справа (слева) в точке а , если правое (левое) предельное значение этой функции в точке а существует и равно частному значению f(a)

Определение 1: Функция непрерывна в точке , если .

Определение 2: Функция непрерывна в точке , если , .

Определение 3: Функция непрерывна в точке , если .

20. Свойства непрерывных функций, связанные с арифметическими операциями. Локальная ограниченность непрерывной функции

Свойства непрерывных функций:

Теорема 1 (локальная огр.): Пусть функция непрерывна в точке , тогда .

Теорема 2 (отделимость от 0): Пусть функция непрерывна в точке и , тогда . .

Теорема 3 (арифметика непрерывных функций): Пусть , непрерывны в точке , тогда:

1). непрерывна в точке .

2). непрерывно в точке .

3). Если , то непрерывно в точке .

(Доказывается на основе арифметики предела фуекции)

21. Непрерывность сложной функции

Теорема: если функция непрерывна в точке , а функция непрерывна в точке то сложная функция непрерывна в точке .

Доказательство:

Возьмем число >0. Так как функция непрерывна в точке то можно подобрать такое число , что

для любого , такого, что . (1)

А так как функция непрерывна в точке , то для положительного числа можно подобрать такое число , что

для любого , такого, что . (2)

Возьмем любое число такое, что . Тогда в силу (2) число удовлетворяет неравенству , и поэтому в силу (1) 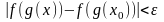. Так как все эти вычисления проведены для любого >0, то непрерывность функции в точке доказана.

22. Непрерывность обратной функции. Непрерывность элементарных функций

Пусть функция y = f(x) задана на сегменте [a, b] , и пусть множеством значений этой функции является сегмент [α, β]. Пусть, далее, каждому y из сегмента [α, β] соответствует только одно значение x из сегмента [a, b], для которого f(x) = y. Тогда на сегменте [α, β] можно определить функцию x = , ставя в соответствие каждому y из [α, β] то значение x из [a, b], для которого f(x) = y. Функция x = называется обратной для функции y = f(x).

Теорема: Пусть на сегменте [a, b] задана строго монотонная непрерывная функция y = f(x), и пусть α = f(a), β = f(b). Тогда эта функция имеет на сегменте [α, β] (или [β, α], если β<α) строго монотонную и непрерывную обратную функцию x =

Доказательство: Множеством значений функции y = f(x) является сегмент [α, β] , а тогда, на сегменте [α, β] существует обратная строго монотонная функция x = , множеством значений которой является сегмент [a, b] и которая поэтому непрерывна на сегменте [α, β]

Простейшими элементарными функциями обычно называют линейную (y=kx+b), квадратичную (y=ax²+bx+c), степенную (y=xⁿ, где n целое число, не равно 1), показательную (y=a^x,где a больше 0 и не равно 1), логарифмическую (y=log_a x, где a больше 0 и не равно 1), тригонометрические (y=sin x, y=cos x, y=tg x, y=ctg x), обратные тригонометрические (y=arcsin x, y=arccos x, y=arctg x, y=arcctg x).