14. Понятие функции. Способы задания функции

Если каждому значению переменной х из множества { X } ставится в соответствие по известному закону некоторое число y , то говорят, что на множестве { X } задана функция

y = y(x) или y = f(x).

Множество { X } всех значений, которые может принимать данная переменная величина, называется областью изменения этой переменной величины.

Переменная x называется аргументом, а множество { X } областью задания функции

y = f(x).

Число y, которое соответствует данному значению аргумента x, называется частным значением функции в точке x . Совокупность всех частных значений функции образует вполне определенное множество {Y}, называемое множеством всех значений функции.

Способы задания функции:

• Аналитический способ – посредством формул

• Табличный способ – посредством задания таблицы отдельных значений аргумента и соответствующих им значений функции

• Способ интерполяции – заключается в замене функции между ее табличными значениями какой-либо простой функцией

• Графический способ – посредством графика

15. Предел функции. Эквивалентность двух определений. Примеры

(Предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении аргумента к данной точке.

Определение 1 (Гейне):

Значение   называется пределом (предельным значением) функции   в точке  , если для любой последовательности точек  , сходящейся к  , но не содержащей  в качестве одного из своих элементов (то есть в проколотой окрестности   ), последовательность значений функции   сходится к 

Определение 2 (Коши):

Значение   называется пределом (предельным значением) функции   в точке  , если для любого наперёд взятого положительного числа ε найдётся отвечающее ему положительное число   такое, что для всех аргументов  , удовлетворяющих условию  , выполняется неравенство  .

Теорема: Определение 1 <=> Определение 2.

Имеем .

.

Возьмем произвольную = =>

.

Обозначим 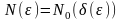. Тогда

0< .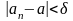

Т.обр.

., то есть

16. Свойства пределов функций, связанных с арифметическими операциями и предельным переходом в неравенствах

Арифметические операции:

Теорема: Если существуют 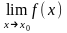и , то:

1). .

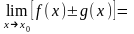
2). = ( - постоянная).

3). * .

4). ,

если .

Доказательство:

Доопределив по непрерывности функции и

в точке ,допустим = и 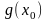= (это изменение функций не влияет на их пределы).

В точке будут непрерывны функции , , , 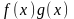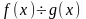(так как = ). Поэтому в силу равенства = получим:

1). = .

2). = =

3). = * .

4). = .

17. Локальная ограниченность функций имеющих предел. Критерий Коши существования предела функции

Теорема: (Локальн. Огр.): Пусть , тогда

, :

.

.

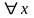
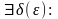
Возьмем Тогда .

Критерий Коши о существовании предела функции.

Определение (условие Коши). Будем говорить, что функция f(x) удовлетворяет в точке a условию Коши, если для любого положительного числа   найдется положительное  (ε), что для любых x₁,x₂, удовлетворяющих условию

0<|x₁-a|< , 0<|x₂-a|< ,

справедливо неравенство

|f(x₁) - f(x₂)|<ε.

Теорема (Критерий Коши): Для того, чтобы существовал предел функции f(x) в точке a ( lim_x ® af(x) = A ) необходимо и достаточно, чтобы f(x) удовлетворяла в точке a условию Коши.