Число e
Сложно
доказать, что функция
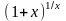при
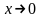имеет
предел. Этот предел обозначается буквой
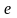в
честь открывшего его петербургского
математика Леонарда Эйлера. Установлено,
что это- иррациональное число и что
=2,718281828459….
Формула, определяющая число
по
традиции называется второй замечательный
предел.
.
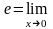Также число
-основание
натуральных логарифмов.
Рассмотрим
.
Докажем, что эта последовательность возрастает и ограничена сверху:
1. Ограниченность.
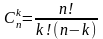-биноминальный
коэффициент
.
+
<
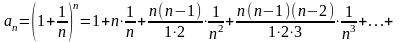
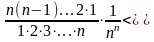
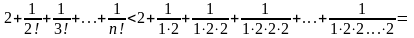
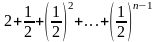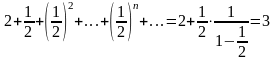
2. Монотонность.
+
.
…
.
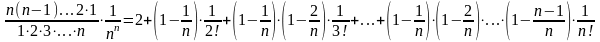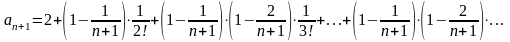
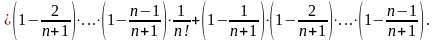
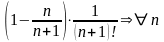
По теореме о монотонности последовательности - сходится.
Принцип вложенных отрезков.
Пусть
=
,
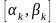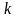=1,2,…,
причем
…,
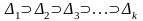то есть
,
.
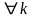
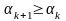Тогда
,
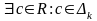то есть
.
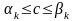Доказательство.
Рассмотрим
,
,
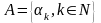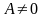ограничено
сверху, так как любое
является верхней границей
множества
в силу вложенности отрезков.
.
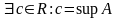Тогда:
а)
-
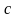верхняя граница
,
то есть
.
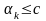б)
-
наименьшая из всех границ, то есть
.
.
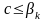Замечание: Если в условиях леммы хотя бы один из концов исключить, то аналогичная лемма будет не верна.
.
(
]
] ] ]
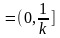0 1/3 1/2 1
Подпоследовательности. Частичные пределы. Теорема Больцано-Вейерштрасса
Определение:
Пусть дана некая последовательность
.
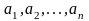Рассмотрим произвольную возрастающую
последовательность целых положительных
чилел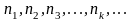
Выберем из последовательности {
},
элементы с номерами
и расположим их в таком же порядке как
:
получим
(
)
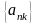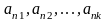- подпоследовательность
последовательности
.
Определение:
Если
,
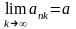то
-
частичный
предел
последовательности
.
Теорема (о частичных пределах сходящейся подпоследовательности): Пусть ,
тогда
.
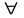Доказательство:
Возьмем произвольный
,
тогда
.
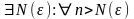
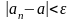Возьмем произвольную
.
Обозначим
.
Тогда
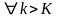имеем:
.
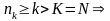
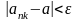Таким образом:
.
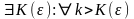Замечание: Понятие частичных пределов для сходящихся последовательностей не нужно.
Теорема Больцано-Вейерштрасса: Из всякой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
Доказательство: Так как последовательность ограничена, то она имеет хотя бы одну предельную точку X. В таком случае из это последовательности можно выделить подпоследовательность, сходящуюся к точке X.
Точка X
называется
предельной точкой последовательности
{
},
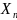если из этой последовательности можно
выделить подпоследовательность,
сходящуюся к X.
Критерий Коши сходимости последовательности.
Теорема (критерий Коши): Числовая последовательность сходится тогда и только
тогда, когда она фундаментальна.
Замечание: Условие необходимости (=>), условие достаточности (<=), критерий- условие
необходимости и достаточности (<=>).
1) Необходимость: (=>).Пусть .
Возьмем произвольный
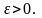Тогда
.
.
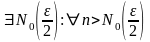
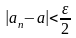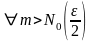
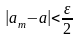Обозначим
,
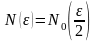тогда
.
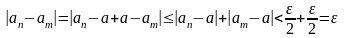фундаментальна.
2) Достаточность: (<=).
1. фундаментальна => ограниченная
.
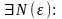
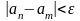Возьмем
,
,
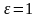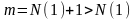тогда
.
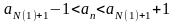Обозначим
.
.
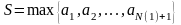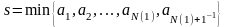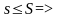ограничена.