
- •Действительные числа. Числовые множества Действия с действительными числами
- •Ограниченные и неограниченные множества
- •Точные грани числовых множеств
- •Числовые последовательности. Ограниченные, неограниченные, бесконечно малые и бесконечно большие последовательности
- •Свойства бесконечно малых последовательностей.
- •Предел числовой последовательности. Единственность предела. Ограниченность сходящейся последовательности.
- •Свойства пределов, связанные с арифметическими операциями над последовательностями
- •Свойства сходящихся последовательностей: предельный переход в неравенствах
- •Монотонные последовательности. Признак сходимости монотонной последовательности
- •Число e
- •1. Ограниченность.
- •2. Монотонность.
- •Принцип вложенных отрезков.
- •Подпоследовательности. Частичные пределы. Теорема Больцано-Вейерштрасса
- •Критерий Коши сходимости последовательности.
- •Понятие функции. Способы задания функции
- •Предел функции. Эквивалентность двух определений. Примеры
- •Свойства пределов функций, связанных с арифметическими операциями и предельным переходом в неравенствах
- •Локальная ограниченность функций имеющих предел. Критерий Коши существования предела функции
- •Бесконечно малые и бесконечно большие функции. Односторонние пределы
- •Непрерывность функции в точке. Примеры непрерывных функций
- •Свойства непрерывных функций, связанные с арифметическими операциями. Локальная ограниченность непрерывной функции
- •Непрерывность сложной функции
- •Непрерывность обратной функции. Непрерывность элементарных функций
- •Замечательные пределы
- •Эквивалентные функции. Символика о и о
- •Классификация разрывов
- •Первая теорема Вейерштрасса
- •Вторая теорема Вейерштрасса
Действительные числа. Числовые множества Действия с действительными числами
I1. Коммутативность
сложения. Для
любых ![]()
a + b = b + a
I2. Ассоциативность сложения. Для любых
a + (b + c) = (a + b) + c
I3. Существование
нуля. Существует
элемент ![]() ,
называемый нулём,
такой, что для любого
,
называемый нулём,
такой, что для любого ![]()
a + 0 = a
I4. Существование
противоположного элемента. Для
любого
существует
элемент ![]() ,
называемый противоположным к a,
такой, что
,
называемый противоположным к a,
такой, что
a + ( − a) = 0
I5. Коммутативность умножения. Для любых
![]()
I6. Ассоциативность умножения. Для любых
![]()
I7. Существование
единицы. Существует
элемент ![]() ,
называемый единицей,
такой, что для любого
,
называемый единицей,
такой, что для любого ![]()
![]()
I8. Существование
обратного элемента. Для
любого ![]() существует
элемент
существует
элемент ![]() ,
обозначаемый также 1
/ a и
называемый обратным к a,
такой, что
,
обозначаемый также 1
/ a и
называемый обратным к a,
такой, что
![]()
I9. Дистрибутивный
закон умножения относительно сложения. Для
любых ![]()
![]()
I10. Нетривиальность
поля. Единица и ноль —
различные элементы ![]() :
:

Между
элементами
определено
отношение ![]() ,
то есть для любой упорядоченной пары
элементов a,
b из
установлено,
выполняется соотношение
,
то есть для любой упорядоченной пары
элементов a,
b из
установлено,
выполняется соотношение ![]() или
нет. При этом имеют место следующие
свойства.
или
нет. При этом имеют место следующие
свойства.
II1. Рефлексивность. Для любого
![]()
II2. Антисимметричность. Для любых
![]()
II3. Транзитивность. Для любых
![]()
II4. Линейная упорядоченность. Для любых
![]()
II5. Связь сложения и порядка. Для любых
![]()
II6.Связь умножения и порядка. Для любых
![]()
Множества
[a, b] – сегмент
(a, b] – полусегмент
(a, b) – интервал
Любой интервал содержащий точку с, будем называть окрестностью точки с
Интервал (с – ε, с + ε), где ε > 0, будем называть ε – окрестностью точки с
Множество всех вещественных чисел будем называть числовой прямой и обозначать символом (-∞, +∞)
[a, +∞) и (-∞, b] – полупрямая
(a, +∞) и (-∞, b) – открытая полупрямая
Ограниченные и неограниченные множества
Определение: Множество Х вещественных чисел называется ограниченным сверху (снизу), если существует такое вещественное число М (число m), что каждый элемент множества удовлетворяет неравенству: x ≤ M (x ≥ m)
При этом число М (число m) называется верхней гранью (нижней гранью) множества Х
Наименьшая
из всех верхних граней ограниченного
сверху множества Х
называется
точной верхней гранью этого множества
и обозначается символом
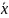 = sup
{X}
= sup
{X}
Наибольшая
из всех нижних граней ограниченного
снизу множества Х
называется
точно нижней гранью этого множества и
обозначается символом
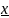 = inf
{X}
= inf
{X}
Точные грани числовых множеств
Точной
верхней гранью
числового множества
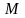 (
(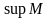 )
называется число
)
называется число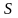 ,
такое что:
,
такое что:
1) S-
верхняя граница
(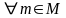
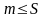 ).
).
2) Для любого
положительного числа
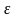 в множестве M
можно найти число
в множестве M
можно найти число
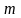 ,
такое что
,
такое что
>
-
.
(
 >
-
)
>
-
)
Точной
нижней гранью
числового множества
(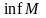 )
называется число
,
такое что:
)
называется число
,
такое что:
1) S-
нижняя граница
(
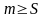 ).
).
2) Для любого положительного числа в множестве M можно найти число , такое что
 +
.
(
+
)
+
.
(
+
)
Теорема
существования:
Пусть
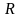 ,
,
 ,
ограниченное сверху (снизу), тогда
существует точная верхняя (нижняя)
грань.
,
ограниченное сверху (снизу), тогда
существует точная верхняя (нижняя)
грань.
Замечание: (аксиома непрерывности множества действительных чисел).
П усть
усть
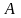 ,
,
и
,
,
и
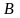 ,
,
причем
,
,
причем
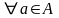 и
и
 :
:
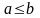 .
Тогда
.
Тогда
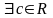 :
:
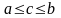 и
.
и
.
, , ограничено сверху.
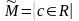
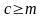
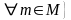 ,
,
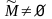 .
.
,
и
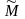 ,
.
,
.
и
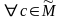

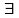
1)
2) > -
Предположим противное:
: .
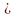 -
-
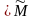 ,
,
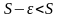 .
Получили
противоречие.
.
Получили
противоречие.
Аналогично для = .
Теорема единственности: Если числовое множество не пусто и ограничено сверху (снизу), то у него есть единственная ( ).
Введем следующие условия:
1)
числовое множество
ограничено
сверху, если можно указать такое число
 ,
что
для всех чисел
из множества
.
,
что
для всех чисел
из множества
.
2)
числовое множество
ограничено
снизу, если можно указать такое число
 ,
что
для всех чисел
из множества
.
,
что
для всех чисел
из множества
.
Доказательство:
Рассмотрим
множество
,
состоящее из всех чисел
,
таких что для любого числа
из
множества
будет
.
Такие числа
существуют, так как множество
ограничено
сверху. В силу непрерывности множества
действительных чисел существует такое
число
 ,
что
,
что
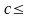 для
любых чисел
(из
)
и
(из
).
для
любых чисел
(из
)
и
(из
).
Покажем,
что
=
.
По определению
,
для всех чисел
из множества
будет
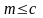 ,
так что первое условие выполнено.
Проверим, что выполнено и второе условие.
Предположим, что оно не выполнено, т.е.
есть такое положительное число
,
так что первое условие выполнено.
Проверим, что выполнено и второе условие.
Предположим, что оно не выполнено, т.е.
есть такое положительное число
 (
>0),
что для всех чисел
из множества
будет
(
>0),
что для всех чисел
из множества
будет
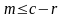 .
Так как
.
Так как
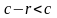 ,
то число
,
то число
 не принадлежит множеству
.
Но это противоречит определению множества
,
которое было множеством всех
чисел
,
таких что для любого числа
из множества
будет
,
а мы нашли число
,
тоже обладающее таким же свойством и
не принадлежащее множеству
.
Полученное противоречие показывает,
что для числа
выполнено
и второе условие из определения верхней
грани.
не принадлежит множеству
.
Но это противоречит определению множества
,
которое было множеством всех
чисел
,
таких что для любого числа
из множества
будет
,
а мы нашли число
,
тоже обладающее таким же свойством и
не принадлежащее множеству
.
Полученное противоречие показывает,
что для числа
выполнено
и второе условие из определения верхней
грани.
