Определение углов сдвига железобетонного элемента
4.28. Угол деформации сдвига определяется по формуле
,
(4.51)
где
- поперечная сила в сечении
от действия внешней нагрузки;
- коэффициент, учитывающий влияние
ползучести бетона и принимаемый равным:
при продолжительном действии нагрузок
где
- см. табл.4.4; при непродолжительном
действии нагрузок
=1,0;
- коэффициент, учитывающий влияние трещин на деформации сдвига и принимаемый равным:
- на участках по длине элемента, где отсутствуют нормальные и наклонные к продольной оси элемента трещины, =1,0;
- на участках, где имеются только наклонные трещины, - =4,0;
- на участках, где имеются только нормальные или нормальные и наклонные трещины, коэффициент определяется по формуле
,
(4.52)
где и - соответственно момент и кривизна от внешней нагрузки при непродолжительном ее действии;
- момент инерции полного приведенного
сечения при коэффициенте приведения
арматуры к бетону
.
Образование наклонных трещин соответствует выполнению условия
.
(4.53)
Примеры расчета
Пример 45.
Дано: железобетонная плита перекрытия
гражданского здания прямоугольного
сечения размерами
=200
мм,
=1000
мм;
=173
мм; пролет
=5,6
м; бетон класса В15 (
=24000
МПа;
=11
МПа,
=1,1
МПа); растянутая арматура класса А400
(
=2·10
МПа) с площадью поперечного сечения
=769
мм
(5
14);
полная равномерно распределенная
нагрузка
=7,0
кН/м, в том числе ее часть от постоянных
и длительных нагрузок
=6,5
кН/м; прогиб ограничивается эстетическими
требованиями.
Требуется рассчитать плиту по деформациям.
Расчет. Определим кривизну в середине пролета от действия постоянных и длительных нагрузок, так как прогиб ограничивается эстетическими требованиями.
Момент в середине пролета равен
кН·м
Н·мм.
Принимаем без расчета, что плита имеет трещины в растянутой зоне, в связи с чем кривизну определим по формуле (4.45). Коэффициент армирования равен
.
При продолжительном действии
нагрузки коэффициент приведения арматуры
равен
.
Из табл.4.5 при
и
находим
=0,43,
а из табл.4.6 при
и
находим соответствующий продолжительному
действию нагрузки коэффициент
=0,13.
Тогда
.
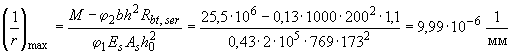Прогиб определим по формуле
(4.33), принимая согласно табл.4.3
:
мм.
Согласно СНиП 2.01.07-85* табл.19, поз.5 определим предельно допустимый прогиб по эстетическим требованиям для пролета 5,6 м путем линейной интерполяции
мм, т.е. условие (4.30) не выполняется.
Уточним прогиб плиты за счет учета переменной жесткости на участке с трещинами путем определения его по формуле (4.34). Для этого определяем момент трещинообразования согласно пп.4.5 и 4.8.
Вычисляем геометрические
характеристики приведенного сечения
при коэффициенте приведения
:
мм
;
мм;
мм
;
мм
.
Заменяя в формуле (4.4) значение на , где согласно табл.4.1 =1,3, определим значение
Н·мм.
Момент в середине пролета от полной нагрузки равен
кН·м.
Тогда при
вычисляем
,
.
Определим кривизну
при
без учета трещин при продолжительном
действии нагрузки, принимая из табл.4.4
для класса бетона В15
=3,4
и следовательно,
МПа.
Поскольку влияние значения на прогиб незначительно, определяем эту кривизну по формуле (4.38), не пересчитывая значение :
.
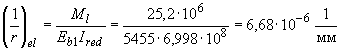Тогда
=
мм
мм,
т.е. уточненный прогиб также превышает допустимое значение.
Пример 46. Дано: железобетонная плита покрытия с расчетным пролетом 5,7 м; размеры сечения (для половины сечения плиты) по черт.4.9; бетон класса В25 ( =30000 МПа, =18,5 МПа, =1,55 МПа); рабочая арматура класса А400 с площадью сечения =380 мм (1 22); постоянная и длительная равномерно распределенная нагрузка =11 кН/м; прогиб плиты ограничивается эстетическими требованиями; влажность окружающего воздуха пониженная ( <40%).
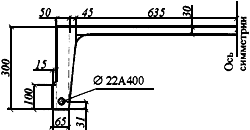
Черт.4.9. К примеру расчета 46
Требуется рассчитать плиту по деформациям.
Расчет. Поскольку приближенная формула для кривизны (4.45) не распространяется на конструкции, эксплуатируемые при влажности воздуха менее 40%, кривизну определяем по общей формуле (4.42) как для элементов с трещинами в растянутой зоне.
Момент в середине плиты от постоянных и длительных нагрузок для половины сечения плиты равен:
кН·м.
Предварительно определяем
момент трещинообразования
согласно пп.4.5 и 4.8. Определим геометрические
характеристики приведенного сечения
при коэффициенте приведения
:
мм
;
мм;
мм
.
Упругий момент сопротивления
мм
.
Заменяя в формуле (4.9) значение
на
,
где
=1,3
(см. табл.4.1), определяем значение
:
Н·мм
Н·мм.
По формуле (4.26) определим коэффициент
.
Приведенный модуль деформации при продолжительном действии нагрузки и при <40% равен
МПа,
и тогда
.
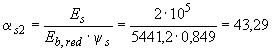Определяем высоту сжатой
зоны по формуле (4.44), принимая усредненную
ширину ребра 85 мм и площадь сжатых свесов
равную
мм
,
и рабочую высоту
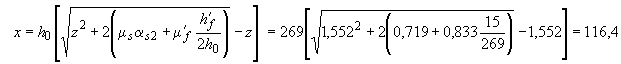мм:
;
;
;
;
мм.
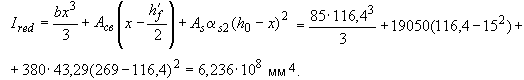
Из формулы (4.42) имеем
.
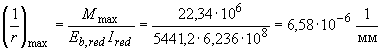Прогиб определяем по формуле (4.33), принимая согласно табл.4.3 :
мм.
Согласно СНиП 2.01.07-85* табл.19, поз.3 предельно допустимый прогиб по эстетическим требованиям для пролета 5,7 м равен =29 мм > =22,3 мм, т.е. условие (4.30) выполняется.