Расчет железобетонных конструкций по деформациям общие положения

4.15. Расчет элементов железобетонных конструкций по деформациям производят с учетом эксплуатационных требований, предъявляемых к конструкции.

Расчет по деформациям следует производить на действие:

постоянных, временных длительных и кратковременных нагрузок при ограничении деформаций технологическими или конструктивными требованиями;

постоянных и временных длительных нагрузок при ограничении деформаций эстетико-психологическими требованиями.

4.16. Значения предельно допустимых деформаций элементов принимают согласно СНиП 2.01.07-85* и нормативным документам на отдельные виды конструкций.

Расчет железобетонных элементов по прогибам

4.17. Расчет железобетонных элементов по прогибам производят из условия

, (4.30)

где - прогиб железобетонного элемента от действия внешней нагрузки;

- значение предельно допустимого прогиба железобетонного элемента.

Прогибы железобетонных конструкций определяют по общим правилам строительной механики в зависимости от изгибных, сдвиговых и осевых деформационных характеристик железобетонных элементов в сечениях по его длине (кривизны, углов сдвига, относительных продольных деформаций).

В тех случаях, когда прогибы железобетонных элементов, в основном, зависят от изгибных деформаций, значение прогибов определяют по кривизне элемента согласно пп.4.18 и 4.19.

4.18. Прогиб железобетонных элементов, обусловленный деформацией изгиба, определяют по формуле

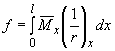, (4.31)

где - изгибающий момент в сечении от действия единичной силы, приложенной в сечении, для которого определяется прогиб, в направлении этого прогиба;

- полная кривизна элемента в сечении от внешней нагрузки, при которой определяется прогиб.

В общем случае формулу (4.31) можно реализовать путем разбиения элемента на ряд участков, определяя кривизну на границах этих участков (с учетом наличия или отсутствия трещин и знака кривизны) и перемножения эпюр моментов и кривизны по длине элемента, принимая линейное распределение кривизны в пределах каждого участка. В этом случае при определении прогиба в середине пролета формула (4.31) приобретает вид

, (4.32)

где , - кривизна элемента соответственно на левой и правой опорах;

, - кривизна элемента в симметрично расположенных сечениях и (при ) соответственно слева и справа от оси симметрии (середины пролета, черт.4.5);

- кривизна элемента в середине пролета;

- четное число равных участков, на которое разделяют пролет, принимаемое не менее 6;

- пролет элемента.

В формулах (4.31) и (4.32) кривизны определяют по указаниям пп.4.21-4.27. При этом знак кривизны принимают в соответствии с эпюрой кривизны.

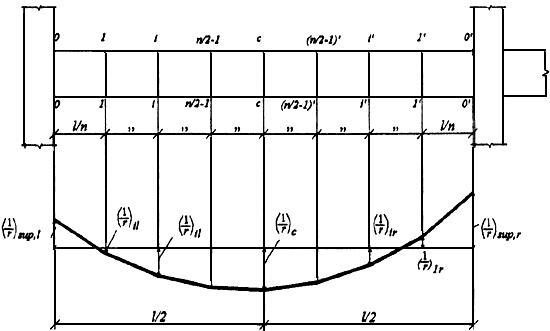
Черт.4.5. Эпюра кривизны в железобетонном элементе при общем случае определения прогиба

4.19. Для изгибаемых элементов постоянного сечения, имеющих трещины на каждом участке, в пределах которого изгибающий момент не меняет знак, допускается вычислять кривизну для наиболее напряженного сечения и принимать для остальных сечений такого участка кривизны изменяющимися пропорционально значениям изгибающего момента (черт.4.6).

Черт.4.6. Эпюры изгибающих моментов и кривизны в железобетонном элементе постоянного сечения

а - схема расположения нагрузки; б - эпюра моментов; в - эпюра кривизны

В этом случае для свободно опертых и консольных элементов максимальный прогиб определяют по формуле

, (4.33)

где - полная кривизна в сечении с наибольшим изгибающим моментом, от нагрузки, при которой определяется прогиб;

- коэффициент, принимаемый по табл.4.3.

Таблица 4.3

#G0Схема загружения свободно опертой балки	Коэффициент	Схема загружения консоли	Коэффициент
Примечание. При загружении элемента сразу по нескольким схемам , где и соответственно коэффициент и момент в середине пролета балки или в заделке консоли для каждой схемы загружения. В этом случае кривизна определяется при значении равном .

Если прогиб, определяемый по формуле (4.33), превышает допустимый, то для слабо армированных элементов ( <0,5%) его значение рекомендуется уточнить за счет учета повышенной жесткости на участках без трещин и учета переменной жесткости на участках с трещинами; для свободно опертых балок, загруженных равномерно распределенной нагрузкой, это соответствует формуле

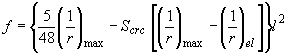, (4.34)

где - полная кривизна в середине пролета, определенная без учета наличия трещин по формуле (4.37);

здесь

- максимальный момент от всех нагрузок;

- момент образования трещин, определяемый согласно пп.4.4-4.8.

Для изгибаемых элементов с защемленными опорами прогиб в середине пролета может определяться по формуле

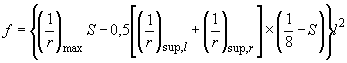, (4.35)

где , , 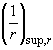- кривизна соответственно в середине пролета, на левой и правой опорах;

- коэффициент, определяемый по табл.4.3 как для свободно опертой балки.

Во всех случаях прогиб принимается не менее прогиба, определенного по кривизнам без учета трещин.

4.20. Для изгибаемых элементов при необходимо учитывать влияние поперечных сил на их прогиб. В этом случае полный прогиб равен сумме прогибов, обусловленных деформацией изгиба (см. пп.4.18 и 4.19) и деформацией сдвига .

Прогиб , обусловленный деформацией сдвига, определяют по формуле

, (4.36)

где - поперечная сила в сечении от действия единичной силы, приложенной в сечении, для которого определяется прогиб, в направлении этого прогиба;

- угол сдвига элемента в сечении от действия внешней нагрузки, при которой определяется прогиб.

Значение определяется по указаниям п.4.28.