Примеры расчета
Пример 10.
Дано: железобетонный прогон кровли с
уклоном 1:4 (
);
сечение и расположение арматуры - по
черт.3.8; бетон класса В25 (
=14,5
МПа); растянутая арматура класса А400
(
=355
МПа);
=763
мм
(3
18);
=0,0;
изгибающий момент в вертикальной
плоскости
=82,6
кН·м.
Черт.3.8. К примеру расчета 10
1 - плоскость действия изгибающего момента; 2 - центр тяжести сечения растянутой арматуры
Требуется проверить прочность сечения.
Расчет. Из черт.3.8 следует:
мм;
мм;
мм;
мм.
По формуле (3.37) определим площадь сжатой зоны бетона :
мм
.
Площадь наиболее сжатого свеса полки и статические моменты этой площади относительно и соответственно равны:
мм
;
мм
;
мм
.
Так как
,
расчет продолжаем как для таврового
сечения.
мм
.
Определим по формуле (3.38) размер сжатой зоны . Для этого вычисляем
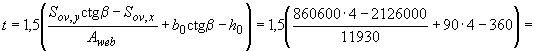
мм.
мм.
Проверим условие (3.39):
мм
мм,
следовательно, расчет продолжаем по формулам косого изгиба.
Проверим условие (3.40) для
наименее растянутого стержня. Из черт
3.8 имеем
мм,
мм;
;
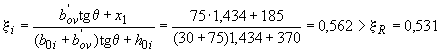(см. табл.3.2).
Условие (3.40) не соблюдается.
Расчет повторим, заменяя в формуле
(3.37) значение
для наименее растянутого стержня
напряжением
,
определенным по формуле (3.41), и корректируя
значения
и
.
МПа
.
Поскольку все стержни одинакового диаметра, новые значения , и будут равны:
мм
;
мм;
мм.
Аналогично определим
значения
,
,
и
:
мм
;
мм
;
мм
;
мм;
мм.
Проверяем прочность сечения
из условия (3.35), принимая
и
кН·м:
Н·мм
Н·мм,
т.е. прочность сечения обеспечена.
Пример 11. По данным примера 10 необходимо подобрать площадь растянутой арматуры при моменте в вертикальной плоскости =64 кН·м.
Расчет. Составляющие изгибающего момента в плоскости осей и равны:
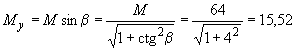кН·м;
кН·м.
Определим необходимое количество арматуры согласно п.3.28.
Принимая значения
,
,
и
из примера 10 при
,
находим значения
и
:
;
.
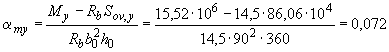Так как
,
расчет продолжаем для таврового сечения.
Поскольку точка с координатами
=0,185
и
=0,072
на графике черт.3.7 находится по правую
сторону от кривой, отвечающей параметру
,
и по левую сторону от кривой, отвечающей
параметру
,
расчет продолжаем с учетом косого изгиба
и полного расчетного сопротивления
арматуры, т.е. условие (3.40) выполнено.
На графике координатам =0,185 и =0,072 соответствует значение =0,20. Тогда согласно формуле (3.42) площадь сечения растянутой арматуры будет равна
мм
.
Принимаем стержни 3 16 ( =603 мм ) и располагаем их, как показано на черт.3.8.
Расчет железобетонных элементов при действии поперечных сил
3.29. Расчет элементов при действии поперечных сил должен обеспечить прочность:
- по полосе между наклонными сечениями согласно п.3.30;
- на действие поперечной силы по наклонному сечению согласно пп.3.31-3.42;
- на действие момента по наклонному сечению согласно пп.3.43-3.48.