2.2 Дві складові щільності розподілу контрольованого параметра

Уведемо в розгляд щільність розподілу системи двох випадкових величин X і X', розуміючи під елементом імовірності ймовірність спільного настання двох подій:

Тоді згідно (1.2) середні ризики виготовлювача й замовника запишемо як подвійні інтеграли

(2.5)

Щільність розподілу контрольованого параметра Х виразиться через як інтеграл по х' у нескінченних межах:

Представимо її у вигляді двох складових

(2.6)

одна з яких відповідає тільки негативному, а інша - тільки позитивному результату контролю:

Інтегрування першої з них по всіх дасть згідно (2.5) середній ризик виготовлювача , інтегрування другої по всіх — середній ризик замовника .Завдання про середні ризики зводиться, таким чином, до пошуку складових і . Ці складові неважко знайти, використовуючи їх імовірнісні вистави

(2.7)

Випадкова величина X' дорівнює сумі випадкових величин Х и Е (7.2) перша з них -X фіксована ( з точністю до dх вона рівна х). Друга залишається випадкової. Це означає, що події

еквівалентні подіям

Увівши відповідну еквівалентну заміну, перепишемо (2.7):

(2.8)

Оскільки прийнята гіпотеза про незалежність випадкових величин Х и Е (див. вище), незалежні й події під знаком імовірності (2.8). Імовірність спільної появи двох незалежних подій дорівнює добутку ймовірностей цих подій, так що

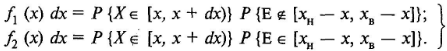(2.9)

Перша ймовірність у записі (2.9) є по визначенню елемент імовірності

(2.10)

Другі ймовірності (назвемо їхніми ваговими множниками негативного й позитивного исходов і позначимо відповідно й ) найдуться як інтеграли від по у відповідних межах

(2.11)

З (2.9) - (2.11) випливає, що кожна зі складових і дорівнює добутку самої щільності розподілу на відповідний ваговий множник результату й .

2.3 Вагові множники кінця середніх ризків

Уведемо в розгляд функцію розподілу випадкової величини Е

Вона дозволяє представити вагові множники в такому виді:

Як і слід було сподіватися, при будь-яких х

і сума складових і дійсно рівна (див. (2.6)).

Поведінка вагових множників показана на рисунку 2.1. У реальних умовах контролю виконуються обмеження (2.4), так що графіки й описуються залежностями, близькими до прямокутних ( П - Образним). Неважко переконатися, що площа під графіком вагового множника позитивного результату дорівнює ширині поля допуску

2.4 Формули середніх ризиків

Їх можна знайти, побравши інтеграли

(2.12)

Рисунок 2.1 - Графіки вагових множників кінця

Обмежимося розглядом найпоширенішого випадку, коли - парна функція, а - симетрична функція із середнім значенням, розташованим по центру норми (поля допуску) - див. (2.1). Тоді в силу симетрії подынтегральных функцій (2.12)

(2.13)

(2.14)

Аналогічними співвідношеннями можна виразити середні ризики й через нижню границю допуску .

По узагальненій теоремі про середнє значення інтегрального вираження (2.13) і (2.14) можна представити у вигляді

(2.15)

(2.16)

де - деяке відхилення від границі допуску.

Неважко переконатися, що інтеграли в правих частинах (2.15) і (2.16) дорівнюють половині середнього арифметичного відхилення погрішності виміру Е:

Покажемо справедливість сказаного для першого інтеграла (див. (2.15)). Позначимо його J . Увівши заміну змінної й проинтегрировав вроздріб, одержимо шуканий результат

Аналогічно запишемо вираження для другого інтеграла, що входить в (2.16).

Отже, середні ризики виготовлювача й замовника з'являються у вигляді компактних співвідношень

(2.17)

прийнятих за їхні розрахункові формули.

Залишається оцінити відхилення . Враховуючи поведінка вагових множників исходов, слід очікувати, що А мало й у першім наближенні їм можна зневажити. Більш акуратної (друге наближення) є отримана нижче оцінка

(2.18)

Покажемо справедливість оцінки (2.18) у випадку рівномірного розподілу погрішності виміру Е.

Звернемося до інтегрального співвідношення середнього ризику замовника (2.14). При рівномірному розподілі погрішності на інтервалі зміни х вагарні множник позитивного результату має вигляд (див. рис.2)

Рисунок 2 - Поведінка вагового множника позитивного результату за верхньою граничною крапкою при рівномірному розподілі похибки вимірів

Рисунок 3 - Кусочно-лінійна апроксимація вагового множника

Розкладемо щільність розподілу контрольованого параметра в ряд Тейлора в околиці верхньої граничної крапки х_в

(2.19)

Для спрощення записів уведемо проміжні позначення

і, обмежившись першими трьома членами розкладання (2.19), знайдемо добуток , яким описується вихідна підінтегральная функція співвідношення (2.14):

Після інтегрування цього результату по х в інтервалу маємо

(2.20)

З іншого боку, розклавши в статечній ряд по результат (2.4.17), знайдений з Використанням узагальненої теореми про середній, одержимо

(2.21)

Сопостаив (2.20) і (2.21), переконаємося, що для збігу їх правих частин з точністю до значення необхідно вибрати рівним

Звідси випливає, що з точністю до відносної погрішності

значення оцінюється співвідношенням (2.18).Аналогічний результат слушний і для середнього ризику виготовлювача. Наведені викладення залишаються в силі.Оцінка розрахункового параметра строго виведена для випадку рівномірного розподілу погрішності виміру Е. Однак її можна поширити й на інші розподіли, оскільки вона виражена через середнє арифметичне відхилення погрішності Е. Можна показати, що на інтервалах своїх істотних змін вагові множники исходов і із задовільною точністю апроксимуються прямими лініями, що відтинають по осі абсцис відрізки довжиною (див. мал. 3).Таким чином, можна зробити деякі висновки. Відомі методи знаходження середніх ризиків виготовлювача й замовника пов'язані із громіздкими обчисленнями й розраховані на повне завдання плотностей розподілу й контрольованого параметра Х и погрішності його виміру Е. Це ускладнює проникнення самих методів в інженерну практику. Істотні незручності вони доставляють і підготовленому фахівцеві-дослідникові. Зустрічаючись із необхідністю вивчення середніх ризиків у різних практичних ситуаціях, зокрема при контролі нових зразків продукції, він може не мати у своєму розпорядженні необхідні закони розподілу. У роботі показане, що в реальних практичних завданнях контролю така докладна інформація, як знання цих законів, необов'язкова.Виведені прості розрахункові залежності, що зв'язують середні ризики виготовлювача й замовника із числовими імовірнісними характеристиками контрольованого параметра Х и погрішності його виміру Е. Для симетрично розподілених Х и Е слушні співвідношення

(2.22)

у яких і - нижня й верхня границі норми (допуску); - середнє арифметичне відхилення погрішності.

Як видне із цих співвідношень, середні ризики не залежать від виду розподілу погрішності Е и повністю визначаються її середнім арифметичним відхиленням . Фактор впливу на них виду розподілу контрольованого параметра X незначний. Досить знати поведінка щільності розподілу у вузькій - околиці границі норми.

Співвідношеннями (2.22) зручно користуватися в дослідницьких цілях, наприклад, коли виникає необхідність порівняльного аналізу ризиків виготовлювача й замовника, коли потрібно оцінити вплив на ризики вимірювальних засобів різної точності й ін. В інженерній практиці, враховуючи малість середнього арифметичного відхилення в порівнянні з розміром норми - , можна використовувати спрощені формули

що дають задовільну точність у більшості практичних завдань контролю.