8. Понятие события и вероятности события.

Всякое действие, явление, наблюдение с несколькими различными исходами, реализуемое при данном комплексе условий, называют испытанием. Результат действия или наблюдения называют случайным событием. Если интересует какое-либо опред-ое событие из всех возможных событий, то его называют искомым событием. Все события будем считать равновозможными, т.е такими, которые имеют равные возможности произойти. События принято обозначать заглавными буквами лат. алфавита: A, B, C, D. События назыв-ся несовместными, если никакие 2 из них не могут произойти в данном опыте вместе. В противном случае события назыв. совместными. Число являющееся выражением меры объективной возможностью этого события и обозначается Р(А). Вероятность события А равна отношению числа m исходов испытаний, благоприятствующих наступлению события А, к общему числу n всех равновозможных несовместных исходов, т.е Р(А)=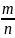 Св-во вероятности: Вероятность любого события есть неотрицательное число, не превосходящее единицы. Действительно число m искомых событий заключено в пределах 0≤m≤n. Разделив обе части неравенства на n получим 0≤Р(А)≤1.

9. Достоверные и невозможные события.

События назыв. достоверным, если оно происходит в данном испытании обязательно. Достоверные события обозн. Буквой u. События назыв. невозможным, если оно в данном испытании не может произойти. Невозможное событие обозн. Буквой V. Полной системой событий А₁,А₂,А₃…А_n назыв. совокупность несовместных событий, наступление хотя бы одного их которых обяз-но при данном испытании. Есть полная система состоит из 2-х событий, то такие события назыв. противоположными и обоз-ся А и А^-. Вероятность достоверного события =1 т.к n/n=1. Вероятность невозможного события =0 т.к о/n=0.

10. Теорема сложения вероятностей.

Суммой конечного числа событий назыв. событие состоящее в наступлении хотя бы одного из них. Сумму 2-х событий обозначают символом А+В или АuВ.

Теорема: Вероятность суммы 2-х несовместных событий = сумме вероятностей этих событий. Док-во: Пусть в результате опыта могут наступить n несовместных исходов, которые по соображениям симметрии будет считать равновероятными. Т.к события А и В несовместны, то не существует таких исходов, которые одновременно благоприятствовали бы и А, и В. Поэтому событию А+В благоприятствуют m_a+m_b исходов. Но Р(А)=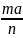 , P(B)= 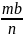,P(A+B)= 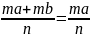+ т.е Р(А+В)=Р(А)+Р(В), что и требовалось док-ать.

Следствие 1. Если события А₁,В₁..., М образуют полную систему, то сумма вероятностей этих событий =1.

Следствие 2. Сумма вероятностей противоположных событий А и А =1.

11. Теорема умножения вероятностей.

Произведением конечного числа событий назыв. событие, состоящее в том что каждое из них произойдёт. Произведение 2-х событий обозначают символом АВ. Пусть А и В-2 случайных события 1-го и того же испытания. Тогда условной вероятностью события А при условии, что наступило событие В, назыв. число

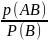
Если обозначить условную вероятность Р(А/В) Р(А/В) то получим формулу 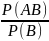(предполагается, что Р(В)не равно 0. Из формулы следует, что Р(АВ)=Р(В)Р(А/В), т.е вероятность произведения 2-х событий = произведению вероятности одного из них на условную вероятность другого при условии что первое событие произошло. Полученная формула имеет смысл, если сущ-ют вероятности событий Р(А/В) или Р(В/А), т.е если события Аи В совместны. Вероятности Р(А) и Р(А/В) различны. Однако возможен случай, когда Р(А/В)=Р(А), тогда событие А назыв. независимым от В. События А назыв. независимым от В, если наступление события В не оказывает никакого влияния на вероятность наступления события А. Учитывая определение независимости событий и правило умножения событий Р(АВ)=Р(В)Р(А/В), получим следующую формулу: Р(АВ)=Р(В)Р(В)Р(А). Теорема: Вероятность одновременного появления 2-х независимых событий, = произведению вероятностей этих событий.