2.3. Порядок выполнения работы

1. Изучить раздел 2.2 настоящих методических указаний.

2. Для варианта, выбранного из таблиц B2.1 и B.2 (Приложение В), выполнить задания 1 и 2.

3.Рассчитать погрешности интерполяции для всех рассматриваемых случаев.

4. Сделать анализ полученных результатов и обосновать полученные решения, дать рекомендации по использованию рассмотренных методов.

3. Составить отчет о выполнении работы.

2.4. Содержание отчета о выполнении работы

1. Цель работы.

2. Постановка задачи.

3. Краткое описание рассматриваемых методов приближения функций.

4. Результаты вычислительного эксперимента.

5. Анализ полученных результатов и выводы об их соответствии теоретически ожидаемым.

6. Приложения.

2.5. Контрольные вопросы

1. Сформулируйте постановку задачи приближения функций. Приведите примеры практического применения решения подобных задач.

2. Что собой представляет задача интерполяции и чем она отличается от задачи аппроксимации?

3. Приведите геометрическую интерпретацию этих задач

4. Какие методы интерполяции Вы знаете?

5. Перечислите достоинства и недостатки известных Вам методов.

6. Как оценить точность решения задачи интерполяции различными методами?

7. Зависит ли точность полученных результатов интерполяции от равномерности размещения узлов интерполяции по числовой оси? Если да, то почему?

8. Что собой представляет задача экстраполяции функции? Чем она отличается от задачи интерполяции?

3. Лабораторная работа №3 «Численное дифференцирование и интегрирование»

3.1. Цель работы

Целью данной лабораторной работы является овладение студентами практическими навыками применения методов численного дифференцирования и интегрирования функций, заданных табличным способом, а также навыков проведения оценок полученных результатов относительно погрешностей и коэффициентов обусловленности.

3.2. Основные теоретические положения и расчетные формулы

Численное дифференцирование применяется тогда, когда функцию трудно или невозможно продифференцировать аналитически. Например, необходимость в численном решении задачи дифференцирования возникает в том случае, когда функция задана таблицей. Кроме того, формулы численного дифференцирования широко используются при разработке вычислительных методов решения многих задач: решения дифференциальных уравнений, поиска решений нелинейных уравнений, поиска экстремума функций и др.

Основные формулы численного дифференцирования:

1. Основанные на первой интерполяционной формуле Ньютона (3.1):

 конечная разность i-го порядка, причем

2. Основанные на первой формуле Гаусса:

(3.2)

2. Основанные на второй формуле Гаусса:

(3.3)

3. Основанные на формуле Стирлинга:

(3.4)

4. Основанные на формуле Бесселя:

(3.5)

Под обусловленностью вычислительной задачи понимают чувствительность ее решения к малым изменениям погрешностей исходных данных.

Задачу называют хорошо обусловленной, если малым погрешностям исходных данных отвечают малые погрешности решения, и плохо обусловленной, если возможны сильные изменения решения.

Мера степени обусловленности вычислительной задачи – число обусловленности. Эту величину можно интерпретировать как коэффициент возможного возрастания погрешностей в решении по отношению к вызвавшим их погрешностям входных данных.

Пусть между абсолютными погрешностями исходных данных X и решения Y установлено неравенство:

(Y^)_ (X^). (3.6)

Тогда величина _ называется абсолютным числом обусловленности.

Если же установлено неравенство:

(Y^)_ (X^), (3.7)

то величину _ называют относительным числом обусловленности.

Для плохо обусловленной задачи >>1.

Несмотря на внешнюю простоту формул численного дифференцирования, их применение требует особой осторожности.

Используемые при численном дифференцировании приближенные значения f^*(X) функции f(X) непременно содержат ошибки измерения или вычисления. Поэтому к погрешности аппроксимации формул численного дифференцирования добавляется неустранимая погрешность, вызванная погрешностями вычисления функции f.

Для того чтобы погрешность аппроксимации была достаточно малой, требуется использование таблиц с малым шагом h. Однако при малых значениях шага h формулы численного дифференцирования становятся плохо обусловленными.

Поясним это на примере.

Полная погрешность для простейшей формулы численного дифференцирования равна:

(3.8)

и представляет собой сумму погрешности аппроксимации

и неустранимой погрешности

. (3.9)

Если  верхняя граница абсолютной погрешности (f^*(X))=|f(X) – f^*(X)|, при вычислении функции f(X).

Тогда неустранимая погрешность оценивается как

(3.10)

Эта оценка означает, что абсолютное число обусловленности _=2/h, и так как _ при h 0, исследуемая формула численного дифференцирования при малых значениях h становится плохо обусловленной.

Формулы для вычисления производных порядка k>1 обладают еще большей чувствительностью к ошибкам задания функций.

Основные формулы численного интегрирования:

а) Пусть отрезок интегрирования [a,b] разбит на n частей с шагом .

Тогда простейшие формулы численного интегрирования имеют вид:

формула левых прямоугольников

(3.6)

формула правых прямоугольников

(3.7)

формула средних прямоугольников

(3.8)

где .

Остаточные члены этих формул соответственно равны

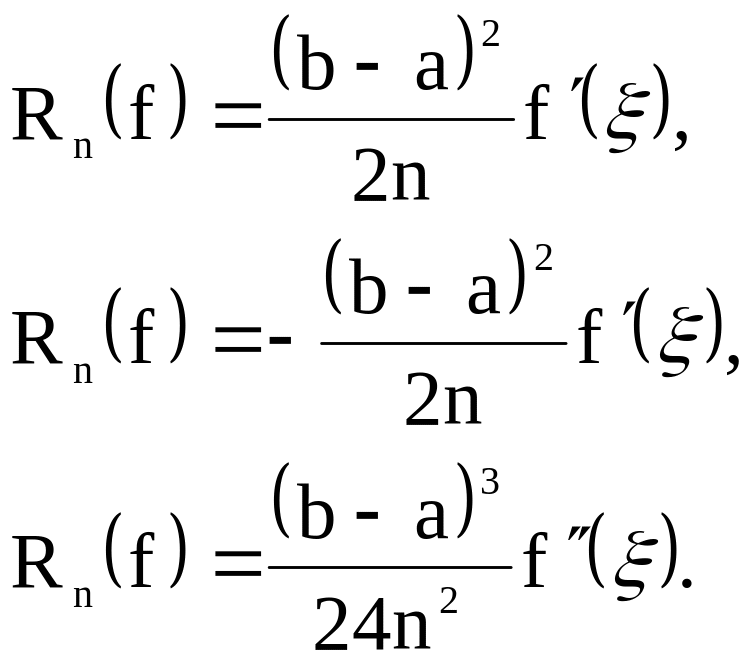(3.9)

где .

б) формула трапеций:

(3.10)

где

причем ;

в) формула Симпсона (число узлов n обязательно четное):

(3.11)

причем

г) формула Ньютона-Котеса для многочлена степени k:

(3.12)

где

Коэффициенты B_k, a_i^(k) и остаточные члены r_k(h) определяют заранее и для них составлена таблица 3.1:

Таблица 3.1 Параметры некоторых частных формул Ньютона-Котеса

k	Bk	a(k)0	a(k)1	a(k)2	a(k)3	a(k)4	a(k)5	rk(h)
1	1/2	1	1
2	1/3	1	4	1
3	3/8	1	3	3	1
4	2/45	7	32	12	32	7
5	5/288	19	75	50	50	75	19
6	1/140	41	216	27	272	27	216
7	7/17280	751	3577	1323	2989	2989	1323
8	4/14175	989	5888	-928	10496	-4540	10496
9	9/89600	2857	15741	1080	19344	5778	5778
10	5/299376	16067	106300	-48525	272400	-260550	427368

д) формула Гаусса:

(3.13)

где

Значения берутся из таблицы 3.2:

Таблица 3.2 Узлов и весов квадратурной формулы Гаусса

n	i	ti	Ci
1	1	t1=0	C1=2
2	1,2	t1,2=0,577350	C1=C2=1
3	1,3 2	t1,3=0,774597 t2=0	C1=C3=5/9=0,555556 C2=8/9=0,888889
4	1,4 2,3	t1,4=0,861136 t2,3=0,339981	C1=C4=0,347855 C2=C3=0,652145
5	1.5 2,4 3	t1,5=0,906180 t2,4=0,538469 t3=0	C1=C5=0,236927 C2=C4=0,478629 C3=0,568889