Линеаризованные уравнения

Для систем более сложных, чем рассмотренные, нелинейные уравнения равновесия настолько сложны, что, как правило, получить их аналитическое решение не удается. Численный же анализ, тоже весьма трудоемкий и сложный, не дает возможности провести качественный анализ поведения систем, подобных рассматриваемой, поскольку проводится для конкретных геометрических и жесткостных параметров.

Поскольку потеря статической устойчивости для большинства конструкций недопустима, нас всегда интересует не столько поведение системы в закритическом состоянии (после потери устойчивости), сколько сами критические точки и соответствующие им критические нагрузки. Их удается найти с помощью приближенных линеаризованных уравнений.

Обратимся снова к Примеру 1.1. Линеаризуем уравнение (1.2), т.е. удержим в разложении (2.4) для только первый линейный член.

. (2.5)

Из (2.5) получаем исходную форму равновесия . Кроме этого решения, справедливого при любом параметре уравнение (2.5) при имеет решение , т.е. - любое, но, разумеется, малое. Таким образом мы определили  .

Уравнение равновесия (1.3) для Примера 1.2 в результате линеаризации принимает вид

(2.6)

и определяет исходную форму равновесия и возможность нетривиального решения при  .

Линеаризованные уравнения позволяют найти точки бифуркации в заранее известных положениях равновесия, но не дают информации ни о характере этих точек, ни о поведении системы в закритическом состоянии, т.е. при больших отклонениях. Поэтому найти с их помощью предельные точки, в которых нет ветвления форм равновесия, строго говоря, невозможно. Однако, и в этих случаях они могут оказаться полезными.

Например, если в Примере1.З угол мал настолько, что допустимо принять

то это тем более допустимо для функций угла . Тогда вместо (2.I) можно рассматривать приближенное выражение

(2.7)

Это уравнение нельзя назвать линеаризованным, поскольку мы удержали и вторые члены разложения (2.4) . Однако анализировать его значительно легче, чем (2.1). При сделанных допущениях вместо (2.2) имеем

Легко видеть, что эта величина меняет знак при

(2.8)

Подставив (2.8) в (2.7), находим приближенные значения критических нагрузок в этих предельных точках

Исследуем с помощью линеаризованных уравнений систему не с одной, а с двумя степенями свободы.

Пример 2.2

Уравнения равновесия cистемы

(2.9)

где усилия в пружинах:

(2.10)

Система (2.9) после подстановки в нее (2.10) и линеаризации примет вид

(2.11)

Кроме тривиального решения , соответствующего вертикальному положению равновесия стержней, система может иметь и нетривиальные решения , если ее определитель:

(2.12)

Корни уравнения (2.12) дают два значения нагрузки (две точки бифуркации).

Пусть для конкретности . Тогда корни уравнения (2.12)

(2.13)

При найденных значениях нагрузки (2.13) уравнения (2.11) совпадают, что позволяет найти лишь соотношения между и .

(2.14)

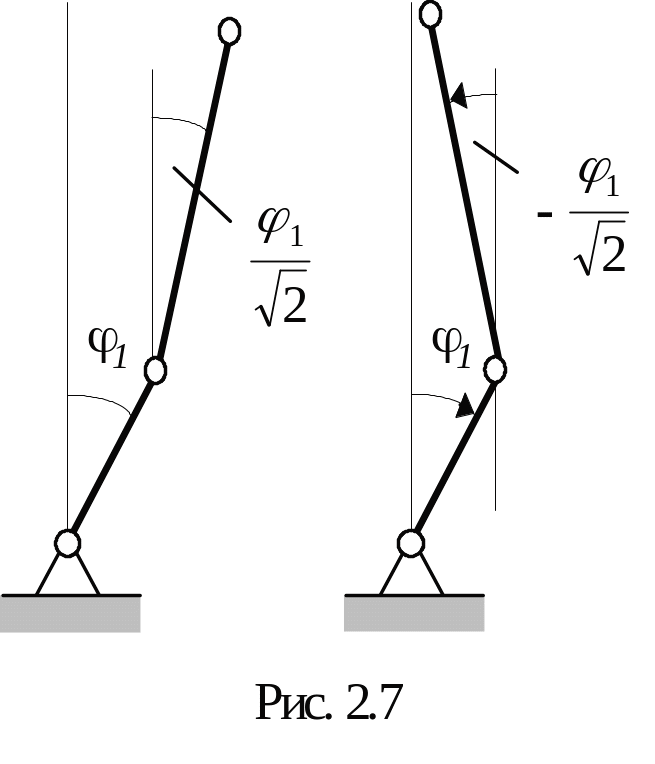
которым соответствуют две формы равновесия, найденные с точностью до множителя (рис. 2.7).

Рассмотренный пример позволяет сделать следующие заключения, характерные для всех задач статической устойчивости.

1. Точки бифуркации находятся из условия нетривиальности решения и математически являются собственными значениями задачи.

2. Количество точек бифуркации совпадает с числом степеней свободы системы, если характеристическое уравнение не имеет кратных корней.

3. Формы отклоненного равновесия математически являются собственными функциями задачи и определяются с точностью до амплитуды.