Устойчивые и неустойчивые состояния равновесия

Под устойчивым принято понимать такое состояние, в которое система возвращается при любых малых от него отклонениях.

Самый простой и наиболее наглядный пример, поддающийся элементарной интуитивной оценке

Обратимся к рассмотренным выше примерам.

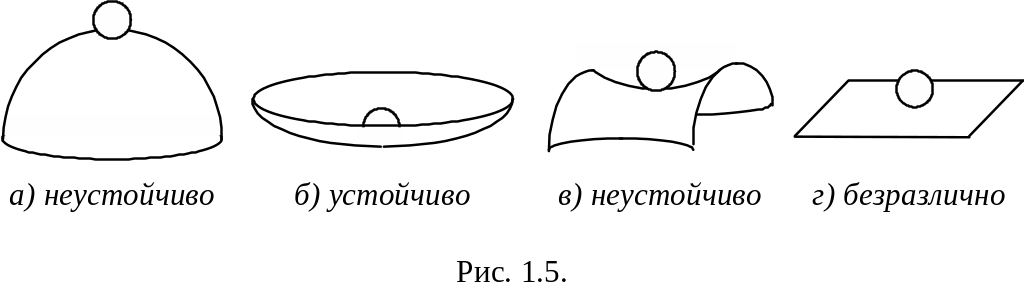
Пример 1.1

.

Для систем с одной степенью свободы Э оказывается функцией одной переменной

. (1.4)

Ее минимум определяется производными

,

. (1.5)

Приравняв нулю первую производную, получаем уравнение равновесия (1.2). Исследуем знаки второй производной в точках, соответствующих решениям уравнения (1.2).

I.

а) при - положение устойчиво.

б) при - положение неустойчиво.

в) при , и надо исследовать знак высших производных.

2.

отклоненное положение устойчиво.

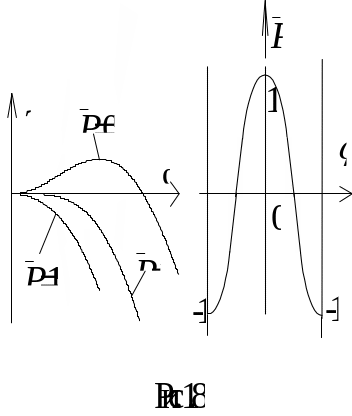
Это иллюстрирует графическая интерпретация той ситуации, которую мы только что рассмотрели.

Здесь, на рис.1.7, показан график зависимости полной энергии системы от смещения .

Показана ситуация при различных значениях параметра нагружения .

По знаку второй производной от энергии по перемещению можно судить об устойчивости или неустойчивости состояния.

Пример 1.2

В отличие от Примера 1

и, следовательно,

,

Исследуем знаки производных от энергии

,

.

Приравняв нулю первую производную, получаем уравнение равновесия (1.3).

По знакам второй производной в точках, соответствующих возможным положениям равновесия, судим о поведении системы и ее равновесии

1.

неустойчиво.

При

равновесие неустойчиво.

2.

- неустойчиво.

3. при

неустойчиво.

Графическая интерпретация свидетельствует об устойчивых состояниях

Особые точки и параметры задачи

Точки, в которых диаграмма нагрузка-перемещение расщепляется на две ветви, называются точками ветвления решения или точками бифуркации.

Для диаграммы, соответствующей примеру 1 (рис.2.1а), это точка .

Если нагрузка достигает , стержень вследствие всегда имеющих место случайных возмущений переходит в отклоненное положение равновесия. С ростом нагрузки отклонение нарастает, вообще говоря, плавно, но в окрестности точки бифуркации малому приращению нагрузки соответствуют достаточно большие смещения.

Иначе ведет себя система в Примере 2. При достижении значения (рис.2.1б) система скачком переходит в нижнее положение равновесия.

Точки в которых положение равновесия становится неустойчивым называются критическими, а соответствующие им значения нагрузок - критическим нагрузками.

При разгрузке системы нижнее положение равновесия остается устойчивым вплоть до , и только здесь происходит перескок. Значения принято называть верхней и нижней критическими нагрузками.

Кроме точек этого типа в теории устойчивости рассматривают также особые точки, характеризующиеся тем, что в них не пересекаются два различных решения, но положение равновесия скачкообразно меняется. Такие точки принято называть предельными.

Пример 2.1

Пусть геометрия системы в ненагруженном состоянии определяется параметрами (рис.2.1), а в состоянии равновесия - параметрами , а также

Полная энергия системы

Положение равновесия определяется условием

(2.1)

Графическая интерпретация уравнения дана на рис.2.3.

При значениях система имеет одно положение равновесия, при - два, а при - три. Для исследования устойчивости системы в этих положениях необходимо оценить знак второй производной от энергии по параметру перемещения.

Аналитически такой анализ довольно трудоемок, но интуитивно ясно, что состояния неустойчивы, поскольку в этих положениях для дополнительного сжатия пружины нужно уменьшить силу .Поэтому при увеличении силы система скачком переходит из точки А в точку А', а при уменьшении силы - из точки В в точку В'.

Таким образом, значения  определяют верхнюю и нижнюю критическую нагрузку.