Числові характеристики випадкових величин
Числові характеристики випадкових величин підрозділяють на характеристики положення і моменти. Визначимо характеристики положення.
Розглянемо
дискретну випадкову величину
X,
що характеризується рядом розподілу.
Нехай
проведемо
N
незалежних дослідів, в яких значення
з’явилось
раз,
раз і т.д.
Очевидно,
що
.
Обчислимо середньоарифметичне
значення
випадкової величини.
(1.5)
У
співвідношенні (1.5) величина
є
частотою події
.
Позначимо
,
тоді
(1.6)
Із
зростанням N
частоти
будуть наближатися до ймовірностей
,
при цьому середньоарифметичне значення
(1.6)
буде
наближатися до значення, яке називають
математичним
очікуванням
випадкової величини:
(1.7)
Для неперервної випадкової величини мат сподівання
(1.8)
Механічною аналогією математичного очікування є абсциса центру тяжіння деякої одиничної маси, неперервну розподіленої вздовж осі абсцис із щільністю f(x).
Модою випадкової величини називають найбільш імовірне значення дискретної випадкової величини, а для неперервної випадкової величини те її значення, при якому щільність розподілу ймовірності максимальна.
Медіана випадкової величини – це таке її значення Ме, для якого р(Х<Ме)=р(Х>Ме).
Геометрична медіана – це абсциса точки, перпендикуляр в якій поділяє площу під кривою розподілу пополам. Перейдемо до розгляду моментів.
Початковим моментом k-го порядку випадкової величини X називається сума
(1.9)
для дискретної випадкової величини і інтеграл
(1.10)
для неперервної величини. Очевидно (див. формули (1.7),(1.8)), що математичне очікування випадкової величини - це її перший початковий момент.
Для моментів (1.9) і (1.10) можна також записати загальний вираз
(1.11)
тобто початковим моментом k-го порядку називається математичного сподівання k-го ступеня відповідної випадкової величини.
Введемо
поняття центрованої випадкової величини
,
яка
зображає
собою
відхилення випадкової величини
від
математичного очікування. Математичне
очікування такої величини дорівнює
нулю, тому що
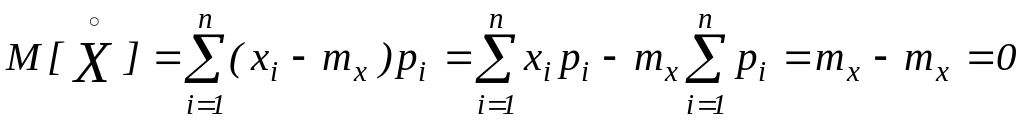(1.12)
Моменти центрованої випадкової величини називають центральними моментами. Ці моменти аналогічні моментам фізичних тіл відносно центра тяжіння в механіці.
Центральним моментом k-го порядку випадкової величини X називається математичне очікування k-го ступеня відповідної центрованої випадкової величини:
Для дискретних випадкових величин
Для неперервних величин
Для будь-якої випадкової величини центральний момент першою порядку дорівнює нулю (1.12).
Другий центральний момент називається дисперсією випадкової величини
і є математичне очікування квадрата відповідної центрованої величини.
Для дискретних випадкових величин
(1.13)
Для неперервних величин
Дисперсія
с характеристикою міри розсіювання
значень випадкової величини відносно
математичного очікування і має
розмірність
квадрата відповідної випадкової
величини. Корінь квадратний із дисперсії
має
розмірність самої випадкової величини
і називається середньоквадратичним
відхиленням (СКВ).
Третій
центральний
момент характеризує асиметрію
кривої розподілу (рис 1.6) і має розмірність
куба випадкової величини. Безрозмірний
коефіцієнт
називається коефіцієнтом асиметрії.
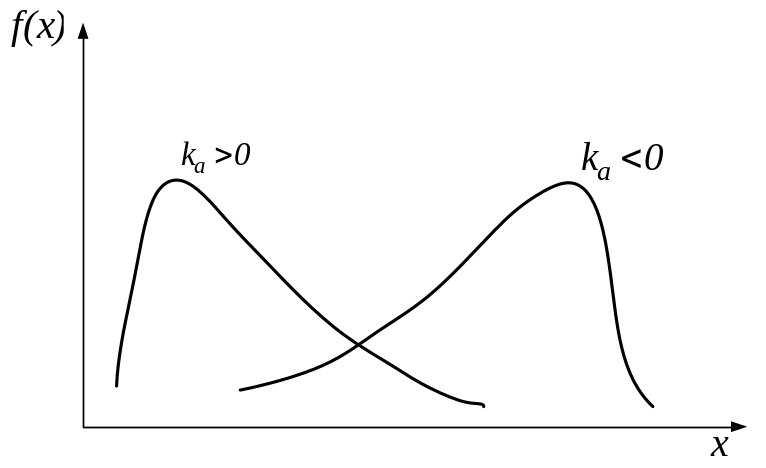
Рис. 1.6. Асиметричні криві розподілу
Четвертий
центральний момент характеризує
гостроверишнність розподілу, а
безрозмірна
величина
називається
ексцесом (рис 1.7).
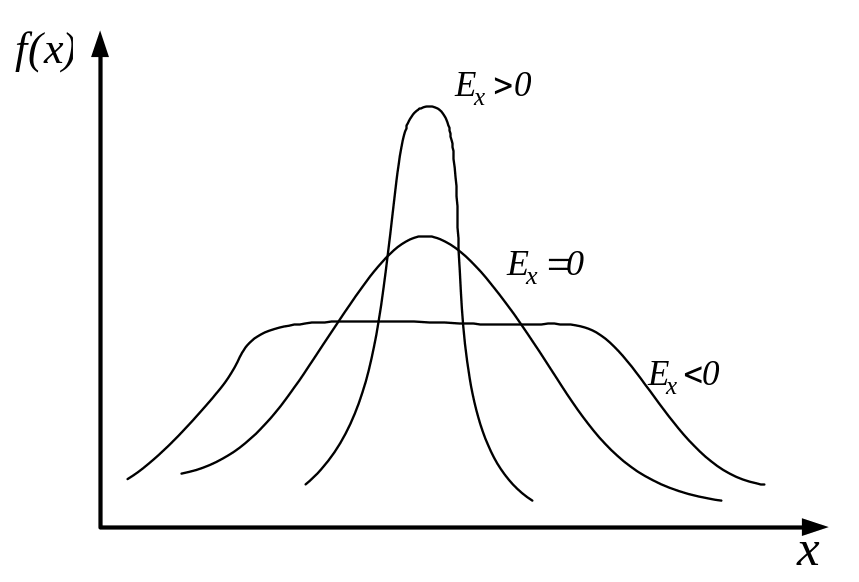Рис.
1.7. Криві розподілу з різною величиною
ексцесу
Далі розглянемо найбільш поширені одновимірні закони розподілу випадкових величин.