Перевод чисел из десятичной системы счисления в двоичную.
Перевод десятичных чисел в двоичную форму можно представить следующей последовательностью пошагового деления на основание двоичной системы счисления.
Пример:
0
0
0
1 0 0 0 
Проверку правильности перевода производят обратными преобразованиями в десятичную систему счисления, для этого используют формулу:
Проверка:
Перевод чисел из десятичной системы счисления в восьмеричную.
Перевод десятичных чисел в двоичную форму можно представить следующей последовательностью пошагового деления на основание двоичной системы счисления.
Пример:
0
0
1 0 0 
Проверка:
Перевод чисел из двоичной системы счисления в восьмеричную.
Для выполнения перевода число в двоичной форме справа налево разбивают на группы из трех цифр, называемых триадами. Если последняя самая левая триада оказалась не полной, т.е. в ней не будет хватать 1 или 2 цифр, то эту триаду необходимо заполнить слева нулями. После этого каждую триаду заменяют соответствующей восьмеричной цифрой.
Пример:
Правило перевода чисел из 2 системы счисления в восьмеричную можно использовать и для перевода из десятичной системы счисления в восьмеричную. Для этого весь процесс осуществляется в два этапа:
1) Перевод десятичных чисел в двоичные;
2) Разбитие двоичного числа на триады, замена триад на соответствующие восьмеричные цифры.
Пример:
1
1
1
0
1
1
0
0
0
1 0 0 0 1 1 0 1 1 1
Перевод из десятичной системы счисления в шестнадцатеричную.
(13)
Перевод чисел из двоичной системы счисления в шестнадцатеричную.
Для выполнения перевода в шестнадцатеричную систему счисления число в двоичной форме справа налево , разбив на группы из четырех цифр, называемых тетрадами. Если последняя, самая левая тетрада оказалась неполной, то ее слева дополняют необходимым числом нулей. После этого каждую тетраду заменяют соответствующей цифрой в шестнадцатеричной системе счисления. Также это правило можно использовать для перевода из десятичной системы счисления в шестнадцатеричную.
Перевод чисел из восьмеричной и шестнадцатеричной системы счисления в двоичную.
Для выполнения перевода из восьмеричной системы счисления в двоичную, каждую цифру восьмеричной системы представляют в виде двоичной триады. Перевод из шестнадцатеричной системы осуществляется аналогично, лишь с той разницей, что шестнадцатеричная цифра представляется тетрадой двоичной цифры.
Двоично-десятичные числа.
Очень часто, для представления двоичного числа используют специальный двоично-десятичный код. При использовании такого кода каждая цифра десятичного числа преобразовывается в свой двоично-десятичный код. Десятичные цифры от 0 до 9 котируются тетрадами от 0000-1001, тетрады от 1010-1111 запрещены, так как используются для представления десятичных чисел больше 9. При обратном переводе каждая вторая тетрада интерпретируется как десятичная цифра.
Все вышесказанное позволяет сделать вывод:
Целое число имеет точный двоичный эквивалент, поэтому целое число в памяти ЭВМ в пределах некоторого диапазона представляется точно.
Правило перевода дробных чисел.
Для того чтобы преобразовать правильную дробь из одной системы счисления в другую, необходимо данную дробь умножить на основание системы в которую осуществляется перевод. В полученном произведении вновь следует умножить дробную часть. Процедура умножения дробной части на основание системы счисления повторяется до тех пор, пока в произведении дробная часть не будет равна нулю или будет достигнута заданная точность. Результат образуется из целой части произведения начиная с первого. Полученные цифры являются цифрами дроби в новой системе счисления. Дробные числа редко переводятся точно, поэтому возникает необходимость задавать точность перевода. Точность перевода – количество знаков после запятой числа в новой системе счисления.
Для перевода из десятичной системы
счисления в двоичную 
Пример:
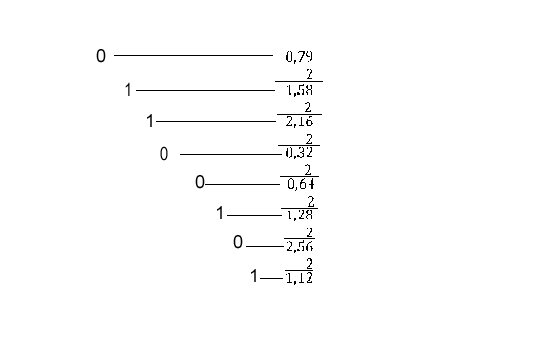
При переводе дробных двоичных чисел в восьмеричные, двоичное число слева разделяются на двоичные триады, при этом к неполной триаде прибавляют справа недостающее число нулей и каждая триада записывается в виде восьмеричной цифры.
При переводе дробных двоичных чисел в шестнадцатеричные, двоичные числа слева разделяются на двоичные тетрады, при этом к неполной тетраде прибавляют справа недостающее число нулей и каждая тетрада записывается в виде шестнадцатеричной цифры.
