3.2 Силовой расчет

Силовой расчет начинается с последней, т.е. наиболее удаленной от ведущего звена группы Ассура, и кончается расчетом ведущего звена.

В качестве примера рассмотрим силовой расчет двухповодковой групп Ассура. На рис.5,а приведена схема двухповодковой группы второго класса первого вида. На звенья 2 и 3 действуют известные силы и моменты. В точках B и D прикладываем неизвестные реакции R₁₂ и R₄₃ отброшенных звеньев 1 и 4 на оставшиеся 2 и 3, условно направляя их вверх. Уравнение равновесия группы имеет вид

Разложим векторы реакций на составляющие по направлениям звеньев (нормальные) и перпендикулярно звеньям (тангенциальные):

; .

Тогда уравнение равновесия примет вид

Составляющие реакции и определяют из условия равновесия звеньев 2 и 3. Для этого составляют уравнения моментов для каждого из звеньев относительно точки C.

Для звена 2

M_C( ) + M_C( ) + M₂ = 0,

откуда

Для звена 3

M_C( ) + M_C( ) + M₃ = 0,

откуда

Составляющие реакций и и полные реакции и определяем из плана сил (рис.5б), построенного на основе уравнения равновесия.

Из начала плана сил (точка а) в некотором масштабе _F проводим вектор силы и из его конца – вектор силы .Из начала вектора и из конца вектора проводим найденные выше силы BC и CD. Из точек d и e проводим линии в направлении сил  и  . Точка f пересечения этих двух линий определит числовые значения и направления сил , , и . Полная реакция во внутреннем шарнире C двухповодковой группы определяется из условия равновесия сил, действующих на звенья 2 или 3:

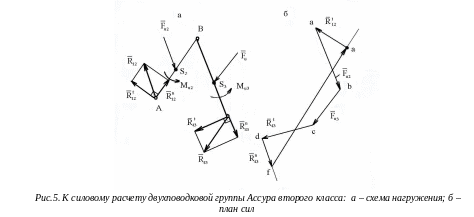
Соединяя точки b и f , найдем реакции .

Расчет ведущего (входного) звена. Это звено входит со стойкой во вращательную или поступательную пару пятого класса Кинематическая цепь статически определима при условии 3n -2p₅ = 0. Ведущее звено при n = 1 и p₅ = 1 не будет находиться в равновесии. Для того чтобы ведущее звено находилось в равновесии, необходимо дополнительно ввести уравновешивающую силу или уравновешивающий момент , которые бы уравновесили все силы и моменты, приложенные к ведущему звену.

На рис.6 представлены два случая расчета реакции во вращательной паре пятого класса О

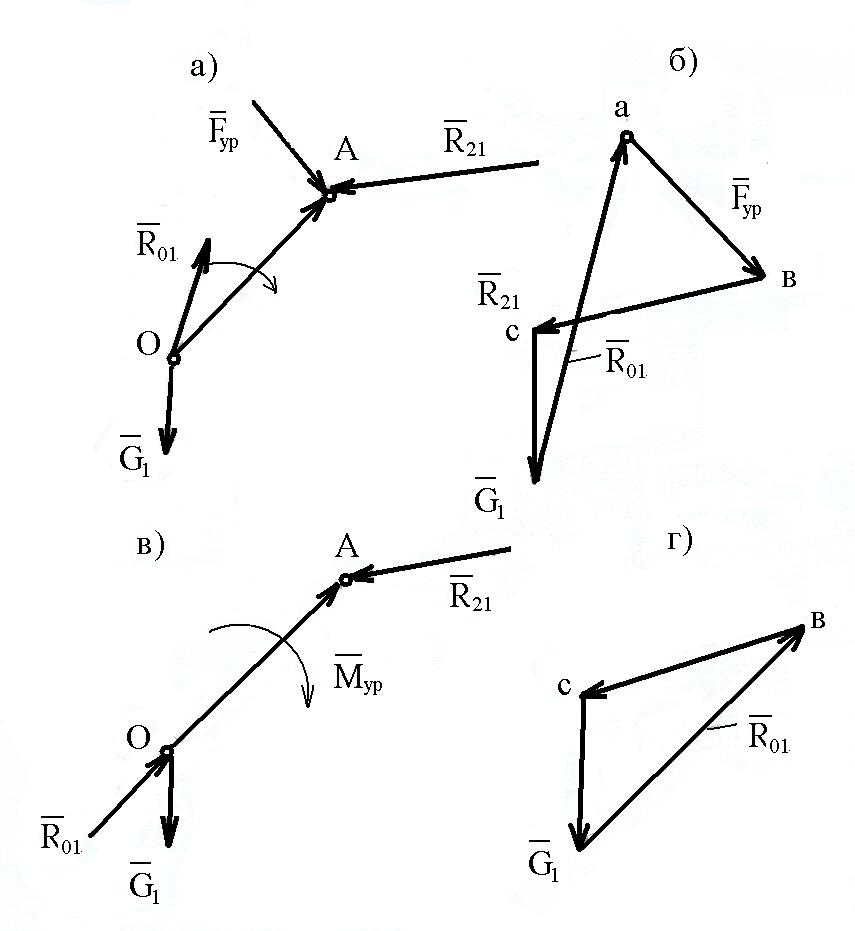
Рис.6. К кинетостатическому расчету ведущего звена:

а- силовое нагружение ведущего звена с уравновешивающей силой; б – план сил при наличие F_ур ; в – план сил при наличие М_ур; г – силовое нагружение с уравновешивающим моментом

В первом случае (рис.6,а) к ведущему звену приложена уравновешивающая сила F_ур, линией действия которой задана. Для ее определения составляем уравнение моментов всех сил, действующих на ведущее звено, относительно точки А:

M_A( + M_A( + M₁ + M_A( = 0,

откуда

M_A( = F_ур = -M_A( + M₁ + M_A( ,

или

F_ур = - M_A( + M₁ + M_A( .

Уравнение равновесия для ведущего звена

Реакция определяется из плана сил (рис.6,б).

Во втором случае (рис.6,б) к ведущему звену приложен уравновешивающий момент M_ур. Из уравнения моментов относительно точки А определяем M_ур:

M_ур+ M_A( + M₁ + M_A( = 0,

Откуда

M_ур = -M_A( + M₁ + M_A( .

Уравнение равновесия для ведущего звена в данном случае имеет вид

.

Реакция определится из плана сил (рис.6д).