2.2. Графоаналитический метод

На практике широко применяют метод планов скоростей и ускорений. Метод основан на графическом решении векторных уравнений движения. Для построения планов скоростей и ускорений механизма должна быть известна его кинематическая схема и задан закон движения входного звена.

В качестве примера рассмотрим кинематику кривошипно-коромыслового механизма (механизма игловодителя швейной машины) (рис.4).

Для заданного положения механизма известны угловые скорости и ускорения входного звена. Для простоты решения задачи будем полагать, что угловое ускорение входного звена равно нулю.

Построение плана скоростей начинается с определения скорости точка А кривошипа

V_A = ω∙l_OA (4)

Вектор скорости V_A направлен перпендикулярно кривошипу ОА в направлении его вращения (угловой скорости). Точка В, принадлежащая звену 2, рассматривается в относительном движении вокруг точки А. Скорость точки В можно представить как векторную сумму скоростей переносного и относительного движений. Переносным движением будем считать скорость точки А, а относительным – вращательное движение звена 2 вокруг точки А .Обозначая последнюю через V_ВА, получаем следующее уравнение для скорости точки В:

, (5)

где  BA, и // ОВ.

Д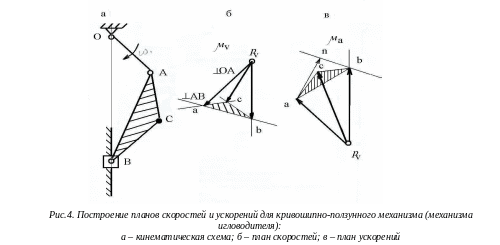 ля определения указанных неизвестных величин строим план скоростей в выбранном масштабе скорости _v. Из произвольного полюса p_v (рис.4,б) проводим вектор р_vа =V_A/_v, перпендикулярный кривошипу ОА, соответствующий на плане скоростей абсолютной скорости V_A. Из конца вектора р_vа (точка а) проводим линию в направлении относительной скорости , перпендикулярную АВ, а из полюса p_v – линию в направлении скорости V_B, параллельную ОВ В пересечении указанных линий находим точку b. Вектор р_vb изображает скорость точки В, а вектор ab – скорость . Значения действительных скоростей находим по формулам:

V_B = _v∙ р_vb и

V_BA = _v∙ ab

Для определения скорости точки С шатуна можно воспользоваться известной из теоретической механики теоремой подобия для скоростей, согласно которой отрезки прямых линий, соединяющие точки на схеме звена механизма и отрезки прямых линий, соединяющие концы векторов относительных скоростей этих точек на плане скоростей, образуют подобные фигуры. Фигура на плане скоростей повернута относительно фигуры схемы звена на 90° (свойство планов скоростей).

Вектор р_vс скорости точки С находим построением на отрезке ab треугольника abc , подобного треугольнику ABC, повернутому на 90°. Для этого из точки а плана скоростей проводим линию, перпендикулярную АС, а через точку b – перпендикулярную ВС. Значение скорости в этой точке вычисляем по формуле

V_C= _v∙р_vс

Угловая скорость звена 2

₂ = V_BA/l_BA

Направление ₂ находится по вектору скорости V_BA.

Планы скоростей механизмов позволяют охарактеризовать движение механизма:

– векторы, выходящие из полюса плана скоростей (р_v) , представляют собой абсолютные скорости;

– вектор, соединяющий концы абсолютных скоростей, представляют собой относительную скорость; он направлен к той точке, которая стоит первой в индексе скорости;

– план скоростей дает возможность находить касательные к траекториям точек механизма, не выстраивая этих траекторий;

– полюс плана скоростей (р_v) соответствует мгновенному центру вращения звена (МЦВ).

Построение плана ускорений начинают с построения абсолютного ускорения a_A точки А кривошипа, складывающегося геометрически из суммы нормальной (a_Aⁿ = ₁²∙l_OA) тангенциальной (a_A^t = ₁∙l_OA) составляющих:

a_A = a_Aⁿ + a_A^t .

При = Выбрав масштаб плана ускорений _a, из произвольной точки p_a (рис.4в), называемой полюсом плана ускорений, откладываем ускорение a_Aⁿ в виде вектора p_aа, направленного от точки А к точке О (рис.4а)

Ускорение точки В находим из уравнения

Значение нормальной составляющей относительного ускорения определяется по формуле

= ₂²∙l_AВ

Вектор направлен по АВ к центру вращения (к точке А механизма) и откладывается из точки а плана. В виде отрезка an = /_a. Направление тангенциальной составляющей вектора будет проходить через конец n вектора и перпендикулярно к нему. Направление абсолютного ускорения точки В известно (а_В // ОВ) и соответствующая линия проходит через полюс р_а.. Пересечение этих двух линий определит положение точки b на плане ускорений, а следовательно, величину ускорения а_В = _a∙р_аb. Вектор ab изображает полное ускорение . Угловое ускорение звена 2 находим по формуле

₂∙= a^t_ВА/l_AВ.

Перенося вектор ускорения в точку В и рассматривая движение точки В относительно точки А, находим направление ₂.

Вектор р_ас ускорения точки С находим, используя свойство плана ускорений, построением на отрезке ab треугольника abc, подобного треугольнику АВС, повернутого на угол (180° - ), где

 = arctg₂/₂²

Значение ускорения в этой точке равно а_C = _a∙р_аc.

План ускорений имеет следующие характеристики:

• векторы, выходящие из полюса р_а плана ускорений, представляют собой абсолютные ускорения соответствующих точек звеньев механизма;

• отрезки, расположенные между концами векторов абсолютных ускорений, соответствуют полным относительным ускорениям;

• концы векторов абсолютных ускорений точек, принадлежащих одному звену механизма, на плане ускорений образуют подобные фигуры, повернутые на угол (180° - );

• план ускорений позволяет находить угловые ускорения звеньев.