1.4. Теореми додавання та множення ймовірностей

Теорема додавання ймовірностей для несумісних подій. Ймовірність суми двох несумісних подій дорівнює сумі ймовірностей цих подій.

Р(А+ В)= Р(А)+ Р(В) (1.8)

Слідство. Ймовірність суми кінцевого числа попарно несумісних подій дорівнює сумі ймовірностей цих подій.

Приклад. В урні знаходяться 3 червоних, 2 білих, 5 синіх однакових за розміром куль. Яка ймовірність того, що куля, яка випадковим чином витягується з урни, буде кольоровою?

Розв’язання. Позначимо, що подія А = {витягання червоної кулі з урни}, подія В = {витягання синьої кулі}. Тоді подія А+B – витягання кольорової кулі. Очевидно, що , .

Застосовуючи теорему додавання для несумісних подій, отримаємо:

Р(А+ В)= Р(А)+ Р(В)= 0,3+ 0,5= 0,8.

Ймовірність події А, обчислена за умови, що подія В вже відбулася, називається умовною ймовірністю події А і позначається

Р(А / В)= P_В(A).

Події А і В називаються незалежними, якщо ймовірність однієї з них не зміниться при настанні іншої. Інакше події А і В називаються залежними.

Теорема множення ймовірностей. Ймовірність добутку двох подій А і В дорівнює добутку ймовірності однієї з них на умовну ймовірність іншої, тобто

Р(АВ)= Р(А)  P_А(В) (1.9)

Теорема множення для незалежних подій. Ймовірність сумісної появи двох незалежних подій А і В дорівнює добутку ймовірностей цих подій:

Р(АВ)= Р(А)  P(В) (1.10)

Події називаються незалежними в сукупності, якщо кожна з них і будь-який добуток останніх (що включає або решту всіх подій, або частину з них) є події незалежні.

Слідство 1. Ймовірність добутку кінцевого числа незалежних в сукупності подій дорівнює добутку ймовірностей цих подій:

(1.11)

Слідство 2. Ймовірність появи кінцевого числа залежних подій дорівнює

, (1.12)

де – ймовірність події за умови, що ., вже настали. Відмітимо, що порядок розташування подій може бути будь-яким.

Приклад. Консультаційна фірма претендує на 2 замовлення від 2 крупних корпорацій. Експерти фірми вважають, що ймовірність здобуття консультаційної роботи в корпорації А дорівнює 0,45. Експерти також вважають, що якщо фірма отримає замовлення в корпорації А, то ймовірність того, що і корпорація В звернеться до них, дорівнює 0,9. Яка ймовірність того, що консультаційна фірма отримає обидва замовлення?

Розв’язання. Позначимо події:

А = {Здобуття консультаційної роботи в кор­порації А}, Р(А)= 0,45;

В = {Здобуття консультаційної роботи в кор­порації В}, P_А(В) = 0,9;

Події А і В — залежні, оскільки подія В залежить від того, станеться чи ні подія А.

Необхідно знайти ймовірність того, що обидві події (і подія А, і подія В) стануться, тобто Р(АВ). Для цього використовуємо теорему множення ймовірностей (1.9):

Р(АВ)= Р(А) P_А(В) = 0,45 · 0,9 = 0,405.

Приклад. На станції відправлення є 8 замовлень на відправку товару: п'ять – усередині країни, а три – на експорт. Яка ймовірність того, що два випадково вибраних замовлення виявляться призначеними для вжитку усередині країни?

Розв’язання. Подія А = {перше узяте випадкове замовлення призначене для внутрішнього вжитку }. Подія В = {друге теж призначене для внутрішнього вжитку}. Нам необхідно знайти ймовірність Тоді за теоремою множення ймовірностей залежних подій маємо

.

Приклад. В урні 5 білих, 4 чорних, 3 синіх кулі. Кожне випробування полягає в тому, що навмання витягують одну кулю, не повертаючи її в урну. Знайти ймовірність того, що при першому випробуванні з'явиться біла куля, при другому – чорна, при третьому – синя.

Розв’язання. Позначимо події

А = {при першому випробуванні з'явиться біла куля},

В = {при другому випробуванні з'явиться чорна куля},

C = {при третьому випробуванні з'явиться синя куля}.

Оскільки повинні відбутися всі події, то мова йде про добуток подій АВС. Крім того, події А, В, С залежні, бо друга куля витягується з тих, що залишилися після відбору першої.

Ймовірність подій А, В, С визначимо за формулою (1.1). Всього в урні n=12 куль. Виходячи з умови, . Оскільки одну кулю вийняли, то в урні залишилося 11 куль і . Аналогічно . За теоремою множення ймовірностей отримаємо:

.

Теорема додавання ймовірностей сумісних подій. Ймовірність суми двох сумісних подій дорівнює сумі ймовірностей цих подій без ймовірності їх сумісної появи.

Р(А+ В)= Р(А)+ Р(В) – Р(АВ) (1.13)

Приклад. Ймовірність отримання прибутку від першої операції дорівнює 0,7, від другої – 0,8. Знайти ймовірність отримання прибутку при підписанні контрактів.

Розв’язання. Позначимо

А = {прибуток від першої операції},

В = {прибуток від другої операції}.

Прибуток буде отриманий від першої, або другої, або від обох операцій, тобто відбудеться подія А+В. Ймовірність отримання прибутку від кожної операції не залежить від результату іншої. Тому події А і В незалежні і сумісні. За теоремою додавання ймовірностей сумісних подій, маємо:

Р(А+ В)= Р(А)+ Р(В) – Р(АВ)= 0,8 + 0,7 – = 0,94.

Теорема (ймовірність появи принаймні однієї події). Ймовірність появи хоч би однієї з подій , ,…, незалежних в сукупності дорівнює різниці між одиницею і добутком ймовірностей протилежних подій , ,…,

(1.14)

Якщо події , ,…, мають однакову ймовірність р, тоді ймовірність появи хоч би однієї з подій , ,…,

Система подій , ,…, називається повною групою подій для даного випробування, якщо будь-яким його результатом є одна і лише одна подія цієї групи. Іншими словами, для повної групи виконуються умови:

1. подія 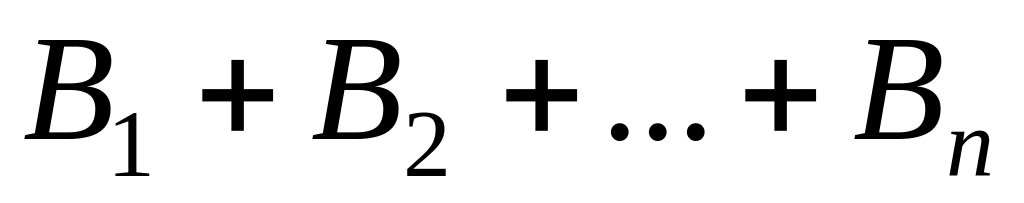достовірна;

2. події і (i  j) попарно несумісні.

Сума ймовірностей подій повної групи дорівнює одиниці.

Приклад. Ймовірності повернення позики в банк трьома клієнтами відповідно дорівнюють: ; ; . Знайти ймовірність повернення хоча б однієї позики.

Розв’язання. Позначимо подію А = {повернення хоч би однієї позики}.

Знаходимо ймовірність неповернення позики для кожного клієнта: ; ; . Застосовуючи формулу (1.14), отримаємо: .

Приклад. Вакансії, що пропонуються безробітним біржею праці, задовольняють першому безробітному з ймовірністю 0,02, другому – з ймовірністю 0,05, а третьому – з ймовірністю 0,1.

Яка ймовірність того, що:

- усі три знайдуть роботу;

- тільки один знайде роботу;

- тільки два знайдуть роботу;

- не менш як два безробітних знайдуть роботу;

- принаймні один.

Розв’язання.

1. Подія А = {усі три знайдуть роботу}.

Цю подію можна подати як добуток трьох подій де і-тий безробітний знайде роботу. Ймовірність події А обчислюємо так:

2) Нехай згідно з умовою можуть відбутися події , які полягають відповідно в тому, що перший, другий і третій безробітні знайдуть роботу.

Подія В = {тільки один із трьох безробітних знайде роботу}.

Цю подію можна подати так: Групи подій, сумою яких є подія В, несумісні між собою, а події в кожній групі незалежні. Тому ймовірність події В обчислимо так:

3) Подія С = {тільки два із трьох безробітних знайдуть роботу}. Подамо цю подію через події та протилежні до них:

Подію С подано як суму несумісних груп подій. У кожній групі події незалежні. Знайдемо ймовірність події С:

4) Нехай подія D = {серед трьох безробітних не менш як два знайдуть роботу}. Тоді її можна подати як суму двох подій: = {серед трьох безробітних два знайдуть роботу і один не знайде} і А = {усі три знайдуть роботу}.Тому маємо:

5) Подія К = {із трьох безробітних принаймні один знайде роботу}. Протилежна подія - «усі три безробітних не знайдуть роботу». Ймовірність цієї події

або .