1.6. Повторні незалежні випробування

Події називаються повторними, якщо в кожному з них настає одна і та ж подія А з однією і тією ж ймовірністю р.

Нехай відносно деякої випадкової події А проводиться n незалежних випробувань. Всі випробування проводяться в однакових умовах, через що ймовірність настання події А залишається однаковою в кожному випробуванні. Ймовірність того, що подія А відбудеться в кожному з незалежних випробувань, позначають а ймовірність настання протилежної події

Ймовірність однієї складної події, яка полягає в тому, що в n випробуваннях подія А настане m разів і не настане n-m разів дорівнює

Таких складних подій може бути стільки, скільки можна скласти сполучень .

Формула Бернуллі. Ймовірність того, що в n незалежних випробуваннях, в кожному з яких ймовірність появи події дорівнює р, подія настане m разів (байдуже в якій послідовності), дорівнює:

_(1.17)

Формулою (1.17) зручно користуватися, якщо (при великих n розрахунки ускладнюються).

Як наслідок з формули Бернуллі, ймовірність того, що подія настане:

а) менше m разів;

б) більше m разів;

в) не менше m разів;

г) не більше m разів;

д) від m₁ до m₂ разів;

відповідно дорівнює:

а) ;

б) ;

в) ;

г) ;

д) .

Сума усіх ймовірностей P_n(m) (де m = 0, 1, 2, ., n ) дорівнює одиниці.

Приклад. Середній відсоток неповернення в строк кредиту, що видається банком, складає 10%. Знайти ймовірність того, що при видачі банком 9 кредитів проблеми з поверненням виникнуть в жодному випадку (тобто усі кредити будуть повернені); не більш як у двох випадках; 3) принаймні в одному випадку.

Розв’язання. Маємо схему дев’яти незалежних випробувань. Нехай подія А — «кредит не повернений», тоді Ймовірності обчислюватимемо за формулою Бернуллі:

1. 

2. Подію «із дев’яти кредитів не більш як з двома виникли проблеми» можна розглядати так:

3. Протилежною для цієї події буде  «усі кредити повернені». Обчислимо цю ймовірність:

Найімовірніше число появи події. Число появи події А в n незалежних повторних випробуваннях називається найімовірнішим числом (появи цієї події), якщо їй відповідає найбільша ймовірність. Вона визначається за формулою:

_(1.18)

Розподіл може мати одне або два найімовірніші числа.

Зауваження: Число  це ціле число.

Приклад. Частка довгих волокон у партії бавовни становить у середньому 0,6 загальної кількості волокон. Скільки потрібно взяти волокон, щоб найімовірніше число довгих волокон серед них дорівнювало 40?

Розв’язання. Скористаємося формулою, за якою визначається найімовірніше число: Підставимо сюди значення відомих величин:

Задача має два розв’язки: n = 66 i n = 67.

Формула Пуассона. Якщо в кожному з n незалежних повторних випробувань , тоді

, де . (1.19)

Приклад. До банку надійшло 5000 пачок грошових знаків. Ймовірність того, що пачку неправильно укомплектовано, дорівнює 0,0004. Знайти ймовірність того, що серед одержаних пачок буде 3 неправильно укомплектованих.

Розв’язання. Якщо подія А = {пачку неправильно укомплектовано}, то її ймовірність р = 0,0004. Розглядається схема незалежних випробувань n=5000, m = 3. Ймовірність події А досить мала, тому задачу розв’я­жемо за формулою Пуассона:

Виконуючи обчислення, знаходимо:

Локальна теорема Лапласа. Ймовірність того, що в n незалежних випробуваннях, у кожному з яких Р(А) = р, подія А відбудеться m раз, подається такою наближеною залежністю:

де , . (1.20)

Локальна теорема Лапласа дає змогу обчислювати ймовірності , якщо n > 10 i p > 0,1.

Функцію називають функцією ймовірностей або функцією Гауса.

Значення визначають за Додатком 1. При цьому – парна функція, тобто (– х) = .

Приклад. За результатами перевірок податковими інспекціями встановлено, що 90% підприємств регіону мають порушення фінансової дисципліни. Знайти ймовірність того, що серед 400 підприємств 350 з них будуть мати порушення фінансової дисципліни.

Розв’язання. Подія А = {підприємство регіону має порушення фінансової дисципліни}. За умовою Р(А) = р = 0,9. Проведено n = 400 незалежних перевірок. Розв’яжемо задачу за формулою локальної теореми Лапласа: Підставляючи дані за умовою задачі, дістаємо:

За таблицями (додаток 1) знаходимо беручи до уваги, що – парна функція.

Отже,

Інтегральна теорема Лапласа. Ймовірність того, що подія А відбудеться від до раз при проведенні n незалежних випробувань, у кожному з яких подія А відбувається з ймовірністю р, подається формулою:

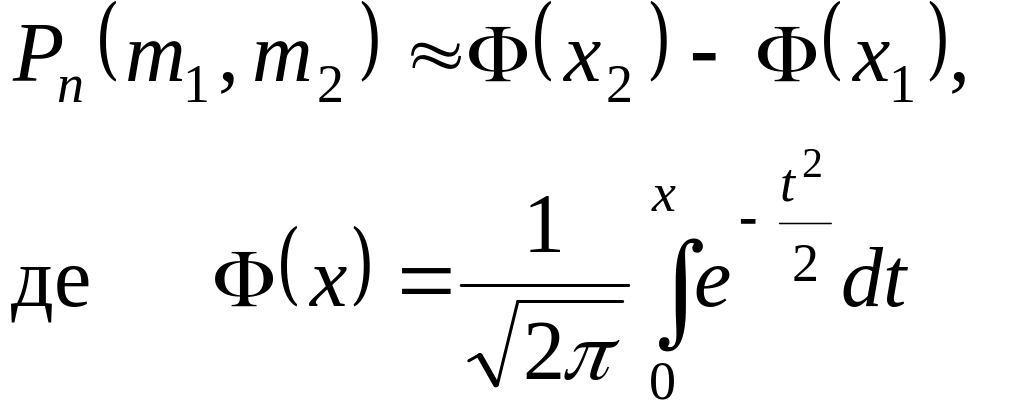_{; (1.21)}

Функція Ф(х) називається функцією Лапласа.

Значення функції Лапласа визначають за Додатком 2. При цьому Ф(х) – непарна функція, тобто Ф(-х) = -Ф(х). При значеннях аргументу х  5 значення функції Ф(х) = 0,5.

Приклад. За результатами перевірок податковими ін­спекціями встановлено, що в середньому кожне друге мале підприємство регіону має порушення фінансової дисципліни. Знайти ймовірність того, що з 1000 зареєстрованих в регіоні малих підприємств мають порушення фінансової дисципліни: а) не менше 480; б) від 480 до 520.

Розв’язання.

а) Подія А = {порушення фінансової дисципліни мають не менше 480 підприємств}. Її ймовірність р = 0,5, кількість незалежних випробувань n = 1000. Застосуємо формулу інтегральної теореми Лапласа:

функція Лапласа, а далі виконаємо обчислення:

Значення функції Лапласа беруться з відповідної таблиці (додаток 2).

б) Подія В = {порушення фінансової дисципліни мають від 480 до 520 підприємств}

Виконаємо допоміжні обчислення: