2.2. Фазовые переходы первого и второго рода.

Опр. Фазовые переходы, сопровождающиеся скачкообразным из­менением физических свойств при непрерывном изменении внешних параметров, называются фазовыми переходами первого рода.

Напри­мер, изменения агрегатного состояния вещества. При фазовых перехо­дах первого рода новая фаза не возникает сразу во всем объеме. Сначала образуются зародыши новой фазы, которые затем растут, распространяясь на весь объем. Температура, при которой происходит фазовый переход, называется точкой перехода.

Встречаются фазовые переходы, при которых превращения про­исходят сразу во всем объеме в результате непрерывного изменения кристаллической решетки. Это может привести к тому, что при опреде­ленной температуре изменится симметрия решетки. Это температура и будет точкой фазового перехода, который в этом случае называется фа­зовым переходом второго рода. Температура, при которой происходит фазовый переход второго рода, называется точкой Кюри.

Понятия фазовых переходов первого и второго рода можно сформулировать и по-иному. Каждое фазовое превращение сопровож­дается скачкообразными изменениями каких-то величин, характери­зующих свойства вещества. Удельный термодинамический потенциал φ (Т, Р) остается непрерывным при любых превращениях. Однако его производные могут испытывать разрыв непрерывности.

Опр. Фазовые превращения, при которых первые производные функции φ (Т, Р) меняются скачкообразно, называются фазовыми превращениями первого рода.

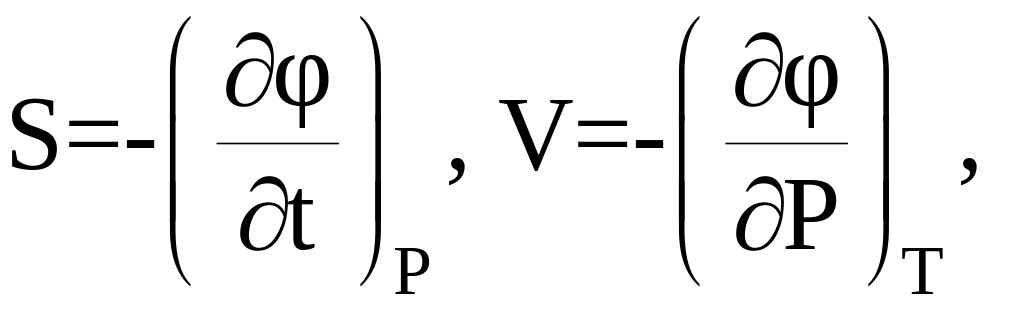(6)

Такие превращения характеризуются скачкообразными изменениями либо удельной энтропии S, либо удельного объема V, либо обеих ве­личин вместе. Скачкообразное изменение S означает, что фазовое пре­вращение сопровождается выделением или поглощением тепла. Отсюда заключаем, что к фазовым превращениям первого рода относятся из­менения агрегатного состояния.

Опр. Фазовые превращения, при которых первые производные функции φ (Т, Р) остаются непрерывными, а вторые производные меняются скачкообразно, называются фазовыми превращениями второго рода.

Из фор­мулы (6) следует, что при таких превращениях величины S и V остаются непрерывными. То есть фазовые превращения второго рода не сопро­вождаются выделением или поглощением тепла, а также изменением удельного объема вещества. Для вторых производных φ (T, P) можно записать:

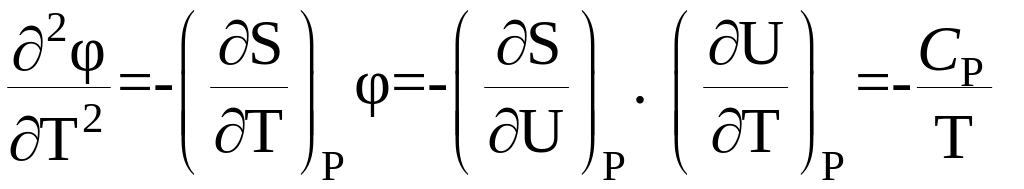
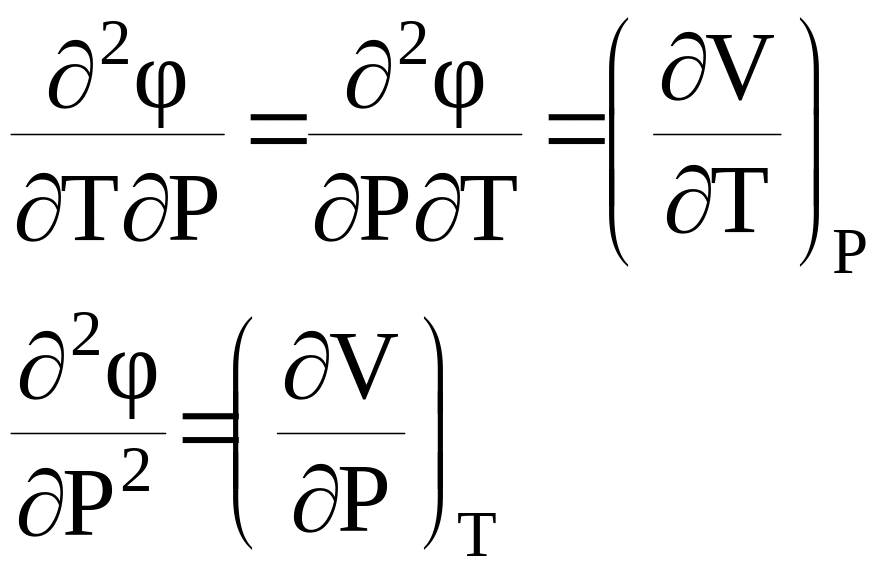
Из этих формул видно, что фазовые превращения второго рода сопро­вождаются скачкообразными изменениями одной или нескольких ве­личин:

1) удельной теплоемкости С_Р ,

2) коэффициента теплового расширения

3) изотермического коэффициента сжатия .

К фазовым превращениям второго рода относится переход сплава из ферромагнитного состояния в парамагнитное, переход в сверхпроводящее состояние и т.д.

Для удельных термодинамических потенциалов вещества в пер­вой и второй фазах можно записать, согласно (4):

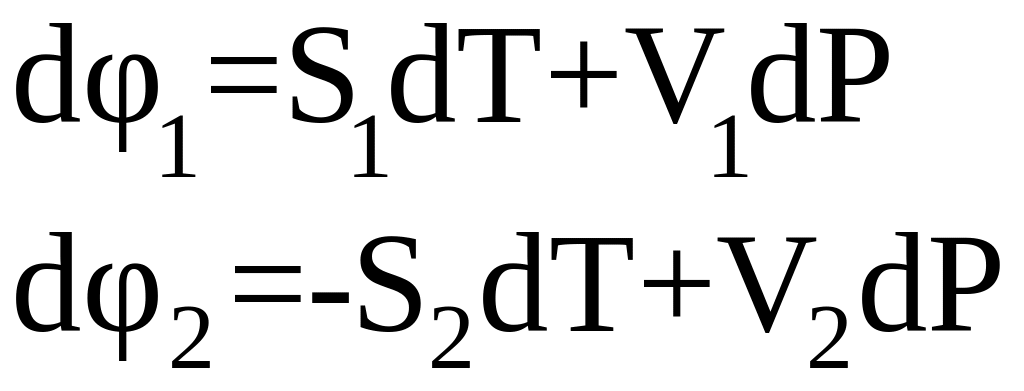
Из условия (5) получаем:

(7)

где

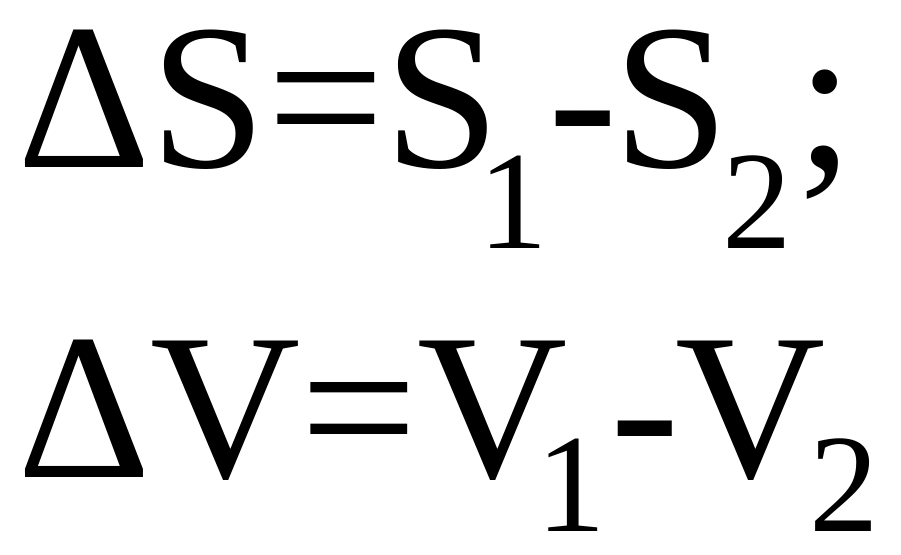
Если фазовые превращения сопровождаются скачкообразными изменениями энтропии, то при таких превращениях поглощается или выделяется теплота, называемая удельной теплотой фазового превра­щения. Например, при переходе единицы массы вещества из газообраз­ного состояния 1 в жидкое 2 выделяется тепло

(8)

При переходе из 2 в 1 такое же тепло поглощается.

Подставим ∆S из выражения (8) в выражение (7), получаем:

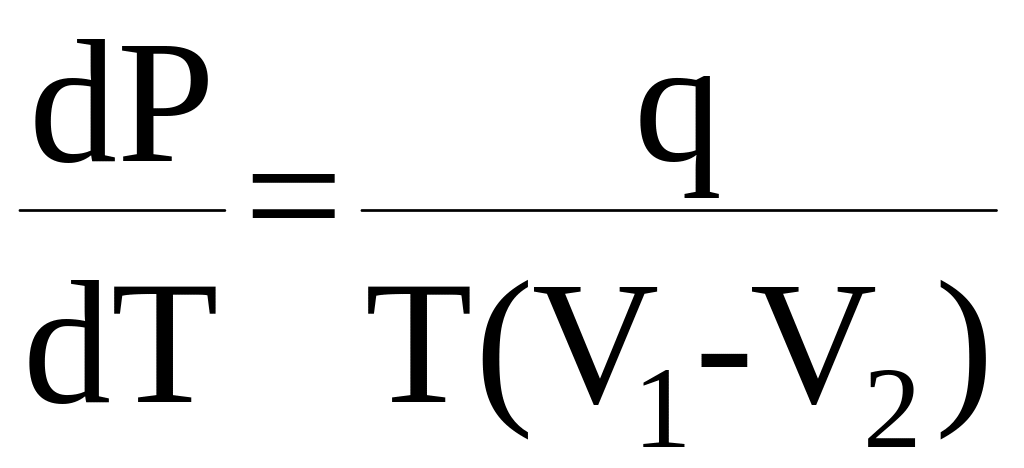(9)

Это важное соотношение называется уравнением Клапейрона - Клаузиуса.