§ 10. Знаходження розв’язків слар.

Вважаємо, що задана сумісна система з m лінійних рівнянь відносно n невідомих. Нехай r – ранг матриці. Оскільки ранг розширеної матриці також дорівнює r, ми виберемо базисний мінор розширеної матриці таким чином, щоб він був розташований в основній матриці системи. Застосовуючи елементарні перетворення стрічок, приведемо розширену матрицю до спрощеного вигляду і дана нам СЛАР згідно тому, що елементарні перетворення стрічок розширеної матриці системи відповідають перетворенню СЛАР в еквівалентну систему, переходить в еквівалентну систему з r лінійно незалежних рівнянь. Будемо вважати, що базисний мінор розташований в перших стовпчиках. Тоді перетворену систему можна записати у вигляді

Тут - елементи перетвореної розширеної матриці. В лівих частинах рівності ми залишили невідомі , які відповідають стовпчикам вибраного базисного мінора, які називаються базисними невідомими, інші невідомі – , які називають параметричними невідомими, перенесено в праві частини рівностей. Очевидно, що присвоївши параметричним невідомим певні довільні значення, знаходимо певні значення базисних змінних, тобто базисні і параметричні невідомі утворюють розв’язок заданої СЛАР.

Тепер очевидно, що якщо стовпчики основної матриці заданої СЛАР є лінійно незалежними і матриця при цьому є квадратною (як у випадку теореми Крамера), то система не може мати двох і більше різних розв’язків. Дійсно, з лінійної незалежності стовпчиків основної матриці слідує, що ранг матриці системи співпадає з кількістю невідомих, отже кількість базисних невідомих співпадає з кількістю невідомих, параметричних невідомих в цьому випадку немає, тому СЛАР має в цьому випадку єдиний розв’язок.

§ 11. Множина розв’язків однорідної системи. Загальний розв’язок системи лінійних рівнянь.

Будь-яка однорідна система лінійних рівнянь сумісна. Вона має розв’язок , який називається тривіальним розв’язком. Всі попередні результати про системи лінійних рівнянь справедливі і для однорідних систем. Попереднє співвідношення у цьому випадку матиме вигляд

Очевидно, що тут оскільки при елементарних перетвореннях стрічок нульовий стовпчик перейде тільки в нульвий.

1.84. Теорема. Якщо стовпчики – розв’язки однорідної системи, то їх сума – також розв’язок цієї системи. Добуток розв’язку однорідної системи на любе число є розв’язком цієї ж системи.

Дано і . Звідси слідує, що

і яким би не було число λ.

Для доведення двох наступних теорем будемо, як раніше, вважати, що базисний мінор матриці системи розташований в перших r стовпчиках.

1.85. Теорема. Якщо ранг матриці однорідної СЛАР відносно невідомихт дорівнює r, то система має лінійно незалежних розв’язків.

Для доведення надамо параметричним змінним x^r+1,x^r+2,…,xⁿ наступні наборів значень:

1) x^r+1 = 1, x^r+2 = 0 . . . xⁿ = 0

2) x^r+1 = 0, x^r+2 = 1 . . . xⁿ = 0

. . . . . . . . . . . .

n – r) x^r+1 = 0 x^r+2 = 0 . . . xⁿ = 1

Для кожного набору значень параметричних невідомих знайдемо відповідні значення базисних невідомих і отримані розв’язки запишемо у вигляді стовпчиків:

Ці розв’язки є лінійно незалежними. Дійсно, складемо матрицю з стовпчикі . Вона має мінор порядку , розташований в останніх стрічках, який дорівнює 1, тому її ранг дорівнює і всі стовпчики є лінійно незалежними.

Сукупність розв’язків називають нормальною фундаментальною системою системою розв’язків.

1.86. Теорема. Нехай – довільна фундаментальна система розв’яків однорідної системи лінійних рівнянь. Тоді любий розв’язок однорідної системи представляє собою лінійну комбінацію розв’язків .

Дійсно, нехай – фундаментальна система розв’язків однорідної системи лінійних рівнянь. Розглянемо стовпчик :

.

В силу того, що лінійна комбінація любого числа розв’язків однорідної системи також є її розв’язком, які б не були числа , стовпчик , який визначається останнім виразом, є розв’язком однорідної СЛАР, яка розглядається.

1.87. Теорема. Якщо – фундаментальна система розв’язків приведеної системи рівнянь, а – деякий розв’язок СЛАР, то стовпчик

при любих числах є розв’язком СЛАР. Навпаки, для кожного розв’язку системи знайдуться такі числа при яких воно має такий вигляд, який називається загальним розв’язком системи лінійних рівнянь.

1.88. Приклад. Знайти фундаментальну система розв’язків (ФСР) та загальний розвязок системи рівнянь

Ранг матриці системи

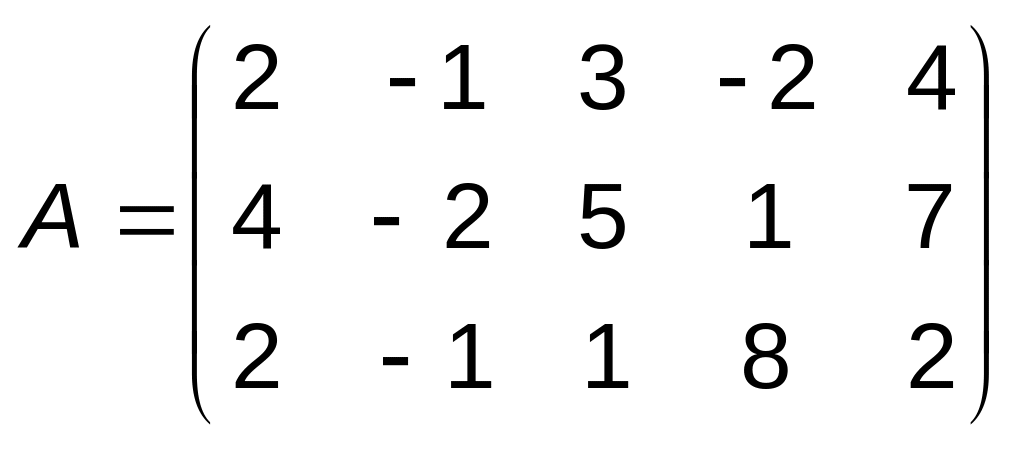
рівний 2 (див. приклад 1.58). Тому вимірність простору рішень даної системи рівна а її ФСР складається з трьох розв’язків. У матриці візьмемо в якості базасного мінора – мінор другого порядку, що складається з чотирьох елементів, в які входять другий та третій елементи першої та другої стрічок

.

Третя стрічка матриці є лінійною комбінацією базасних стрічок, тому останнє рівняння системи є наслідком перших двох рівнянь і його можна відкинути. У перших двох рівняннях члени, що відповідають базисному мінору, залишаємо у лівій частині, а невідомі вважаємо параметричними і переносимо члени з цими невідомими у праві частини рівняннь. У результаті приходимо до системи рівнянь

рівносильній початковій системі, тобто множина розв’язків цієї системи збігається з множиною розв’язків початкової системи.

Знайдемо перший базисний розв’язок . Для цього покладемо , . Попередня система рівнянь при цьому має вигляд

Визначником матриці отриманої системи є відмінний від нуля базисний мінор. Тому така система має єдине рішення, яке можна знайти, наприклад, за формулами Крамера: , . Таким чином 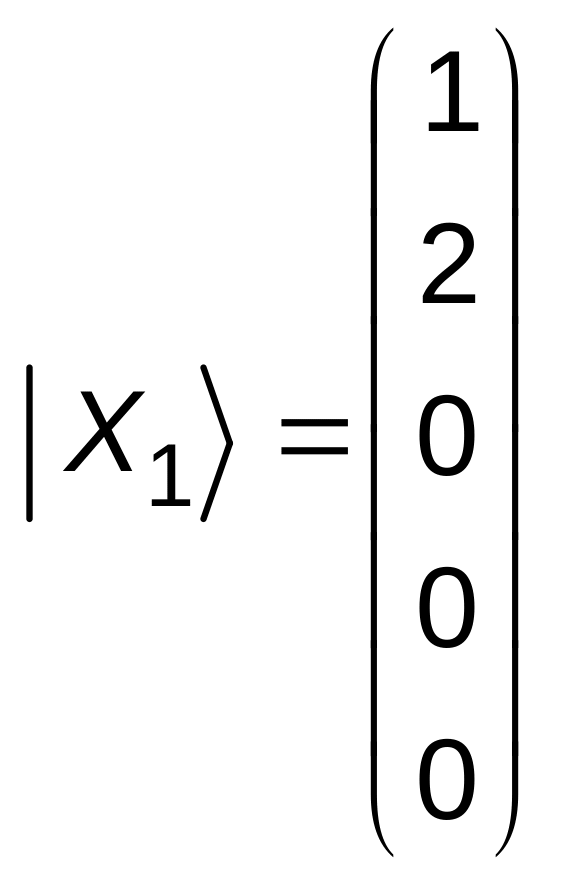. Покладаючи в системі (1) , , , аналогічно знаходимо , , тобто другим базисним розв’язком є стовпчик 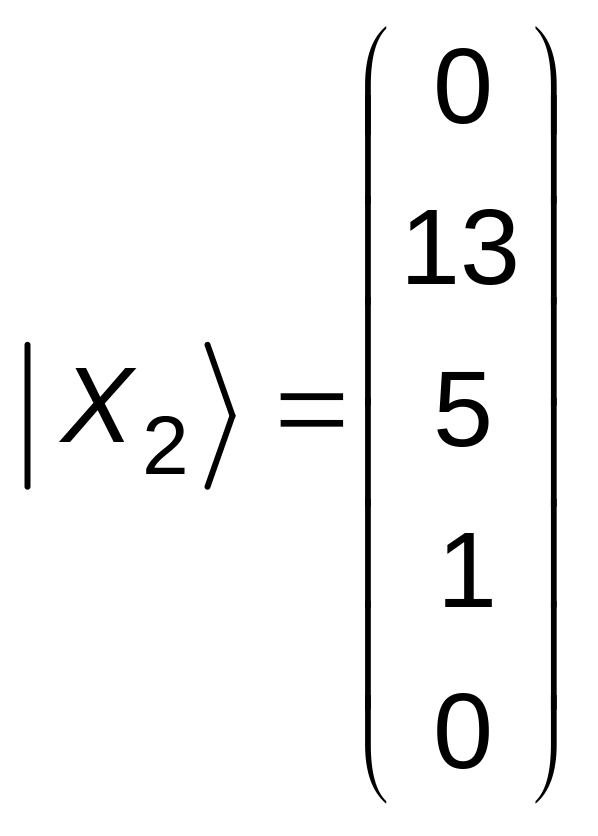. Нарешті, покладаючи , , , знаходимо , . З цього слідує, що третім базисним розв’язком є 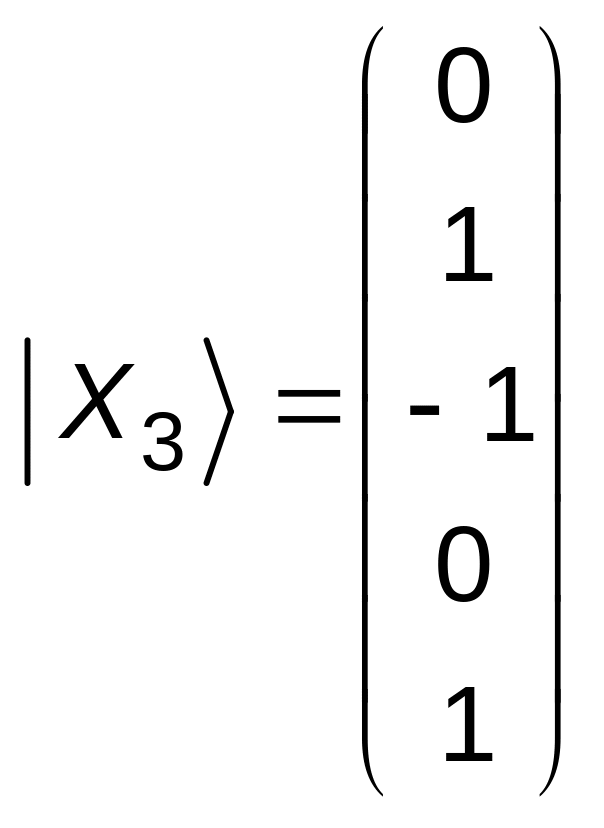. Таким чином ФСР, щоскладається з розв’язків , , , побудована. Відмітимо, що побудована таким чином ФСР називається нормальною ФСР. Підкреслимо, що стовпчики , , , які утворюють нормальну ФСР, є лінійно незалежними оскільки параметричні невідомі , , було обрано так, що мінор третього порядку в матриці з цих стовпчиків

,

відмінний від нуля. Тому ранг цієї матриці рівний 3, тобто рівний числу стовпчиків матриці.

Запишемо тепер загальний розв’язок початкової системи рівнянь:

,

або в координатах.

, , ,

де – довільні константи.

1.89. Приклад. В якості прикладу на основі теореми Кронекера-Капеллі проаналізуємо взаємне розташування двох прямих на площині і в просторі.

Випадок 1. Дві неспівпадаючі прямі на площині. Прямі паралельні, якщо вони не мають спільної точки, тобто якщо

.

В подальших розділах буде показано, що рівняння прямої в просторі можна записати як , де – радіус-вектор будь-якої точки, що належить даній прямій (початкова точка), – направляючий вектор.

Випадок 2. Дві прямі в просторі. Нехай задано дві прямі в просторі і , де і – радіус-вектори початкових точок прямих. і – відповідно направлені вектори прямих. У випадку, якщо вектори некомпланарні, тобто якщо

,

то прямі є мимобіжними. Якщо ж , то прямі або перетинаються або паралельні або співпадають. Для того щоб з’ясувати їх взаємне розташування в цьому випадку дослідимо наступну CΛAР:

Маємо CΛAР з трьох рівнянь відносно двох невідомих і . Очевидно, що ранг і основної розширеної матриць системи не перевищує 2. Очевидно, що прямі перетинаються, якщо і не є колінеарними, тобто в цьому випадку і співпадає з , тобто кількість базисних змінних – 2, параметричних змінних немає, отже дана CΛAР має єдиний розв’язок, який дає значення параметрів , що визначають точку перетину заданих прямих. Якщо прямі паралельні або співпадають, то вектори є колінеарними, тобто , і тоді

Якщо в цьому випадку є не колінеарними з векторами , то тоді прямі паралельні і

тобто СΛАР згідно теоремі Кронекера-Капеллі є несумісною. Якщо ж є колінеарним до , то прямі співпадають, в цьому випадку ранг основної і розширеної матриць СΛАР співпадають і є рівними 1, тобто в цьому випадку СΛАР має безліч розв’язків як і повинно бути.

44