§ 6. Елементарні перетворення як множення матриць. Детермінант добутку.

1.72. Теорема. Кожне елементарне перетворення стрічок матриці А розмірів рівносильно множенню матриці А зліва на деяку квадратну матрицю порядку m.

Розглянемо квадратну матрицю , яка отримується з одиничної матриці порядку перестановкою і-ої та j–ої стрічок. Очевидно, що при множенні матриці розмірів зліва на відповідні стрічки матриці А переставляться.

Нехай – матриця, яка отримується з тієї ж одиничної матриці заміною і-ої одиниці на діагоналі на число . При множенні матриці А зліва на і-а стрічка матриці А помножиться на .

Позначимо через матрицю, яка отримується з одиничної матриці заміною на одиницю нульового елемента, розташованого на перетині і-ої стрічки та j–го стовпчика. Множення матриці А зліва на матрицю рівносильно додаванню j–ої стрічки матриці А до і-ої стрічки. Зауважимо, що , i відмінні від нуля: , , . Матриці , і називають матрицями елементарних перетворень. Якщо матриця А квадратна, то , , отже в цьому випадку для матриць елементарних перетворень справедливо .

Послідовному виконанню елементарних перетворень стрічок матриці відповідає множення зліва на добуток відповідних матриць елементарних перетворень. Елементарні перетворення стовпчиків можемо довести, домножаючи матрицю А справа на аналогічні матриці.

1.73. Припущення. Якщо , то знайдуться матриці елементарних перетворень такі, що .

Якщо , то існує. Так як , то елементарними перетвореннями стрічок матриця може бути перетворена в одиничну матрицю, тобто знайдуться такі , для яких . Очевидно, що .

1.74. Зауваження. Існування оберненої матриці для кожної невиродженої матриці буде доведено в наступному параграфі.

1.75. Припущення. Для любих квадратних матриць А і В одного порядку .

Дійсно, у випадку твердження витікає з оцінки рангу добутку матриць. Якщо , то

→

в силу .

§ 7. Система лінійних алгебраїчних рівнянь.

1.76. Означення. Системою лінійних алгебраїчних рівнянь (СЛАР) називають систему m рівнянь відносно n невідомих x¹, x², … xⁿ наступного виду:

СЛАР може бути записані у більш компактному вигляді за допомогою операції множення матриць.

Нехай

– матриця, елементи якої є коефіцієнти при невідомих у заданій СЛАР і яку називають митрицею системи,

– стовпчик вільних членів, – стовпчик невідомих.

Тоді СЛАР може бути записано як .

Матриця системи, доповнена стовпчиком вільних членів, називається розширеною матрицею системи і позначається 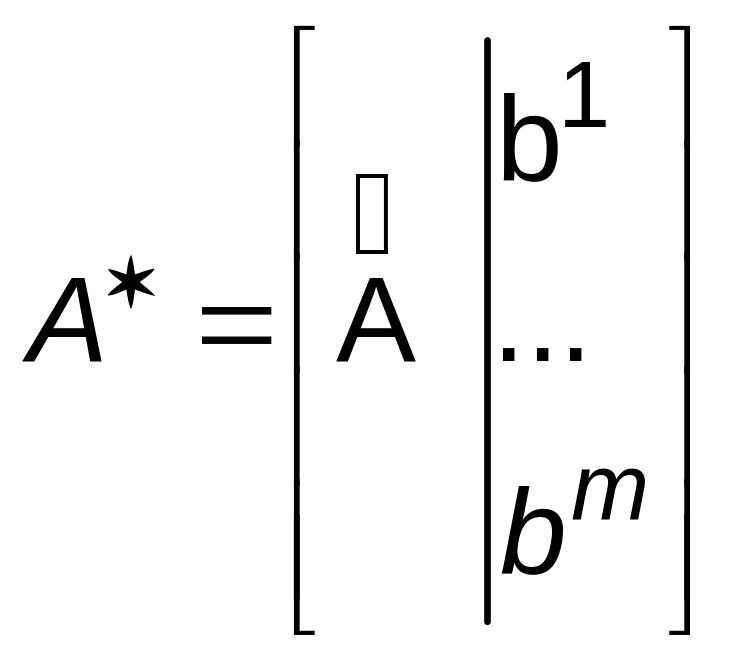. Якщо вільні члени всіх рівнянь дорівнюють нулю, система називається однорідною.

1.77. Означення. Сукупність n чисел називається розв’язком СЛАР, якщо кожне рівняння системи перетворюється в числову рівність після підстановки в нього чисел αⁱ замість відповідних невідомих xⁱ для всіх i = 1, …, n.

Задача полягає в знаходженні розв’язків СЛАР, причому ми не робимо ніяких припущень відносно коефіцієнтів і вільних членів системи і навіть відносно числа рівнянь і числа невідомих. Тому можуть бути різні можливості – система може взагалі не мати рішень або мати їх безліч . Системи, які не мають розв’язків, називаються несумісними, а які мають хоча б один розв’язок – сумісними