§ 3. Методи обчислення детермінантів матриць.

1.43. Означення. Елементарними перетвореннями матриці називаються наступні перетворення:

1. Множення стрічки на число, відмінне від нуля.

2. Додавання до однієї стрічки іншої стрічки цієї ж матриці.

3. Перестановка стрічок матриці.

4 – 6. Ті ж перетворення стовпчиків матриці.

З властивостей визначників слідує, що детермінант матриці не зміниться, якщо до якої-небудь стрічки (стовпчика) добавити лінійну комбінацію інших стрічок (стовпчиків) цієї матриці, що дає можливість знаходити визначник таким чином:

· Метод приведення до трикутного вигляду.

Суть методу – в приведенні за допомогою елементартих перетворень визначника до такого вигляду, коли всі елементи, що знаходяться по одну сторону однієї з діагоналей, дорівнюють нулю. Якщо в першому стовпчику є ненульові елементи , то беремо любий з них – нехай це буде a_k1, і до всіх стрічок, крім k-ої, добавимо k-ту стрічку, помножену на , де – перший елемент стрічки, до якої додають k-у стрічку. Таким способом матриця буде приведена до вигляду, коли всі елементи крім одного в першлму стовпчику дорівнюють нулеві, отже , де – додатковий мінор елемента в перетвореній матриці. Для обчислення застосуємо той же спосіб і через крок визначник буде знайдено.

1.44. Приклад. Знайдемо

.

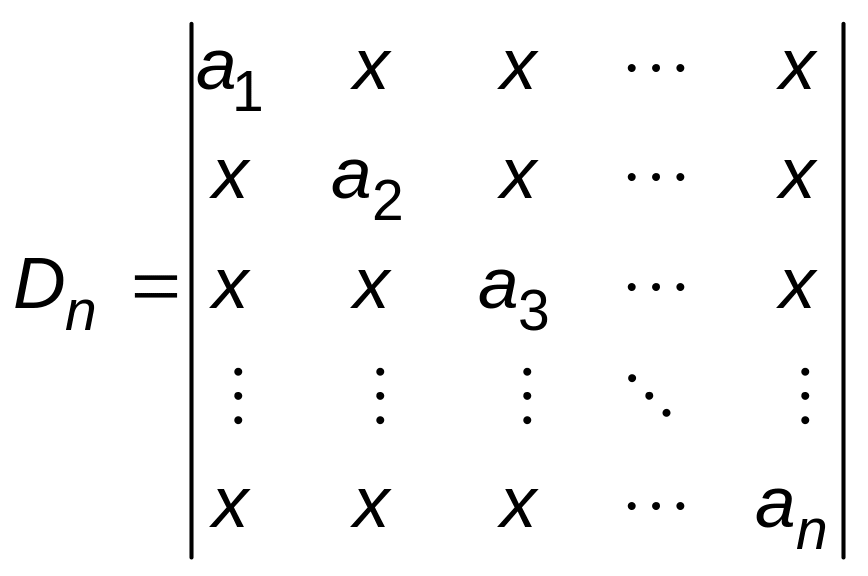Перший крок. Віднімемо першу стрічку від усіх інших

Другий крок. З першого стовпчика виносимо з другого , з третього – , і т. д.

Третій крок. До першого стовпчика додаємо всі інші стовпчики

Четвертий крок. Розкриваємо визначник за першим стовпчиком і отримуємо кінцевий результат

.

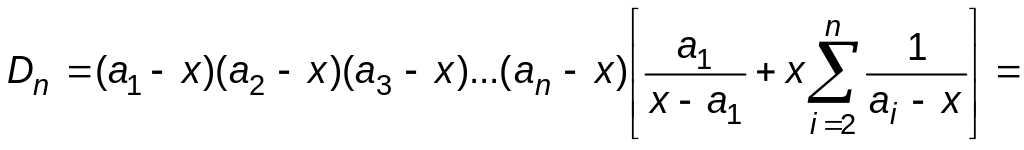
· Метод рекурентних співвідношень.

Метод заключається в тому, що даний визначник обчислюють, перетворюючи і розкладаючи його за стрічкою або стовпчиком, через визначники того ж вигляду, але більш низького порядку. Отримане співвідношення називається рекурентним.

Розглянемо випадок, коли рекурентне співвідношення має вигляд , , і q – незалежні від n величини. Якщо , то , де – визначник 1-го порядку даного вигляду. Нехай , α і β – корні квадратного рівняння , тоді , отже

.

Аналогічно

.

Таким чином

Розглянемо два випадки.

Випадок 1. тоді маємо ,

, тому , звідки

.

Випадок 2. . В цьому випадку маємо:

і так далі по аналогії

1.45. Приклад.

Розкладемо за елементами 1-го стовпчика:

Наступний крок – розкладемо визначник за 1-ою стрічкою і отримуємо: , отже на основі отриманих раніше співвідношень обчислення даного визначника зводиться до пошуку корнів рівняння .

Часто при обчисленні визначників зручно комбінувати обидва вищевказані методи. Як приклад, розглянемо обчислення визначника Вондермонда.

1.46. Приклад.

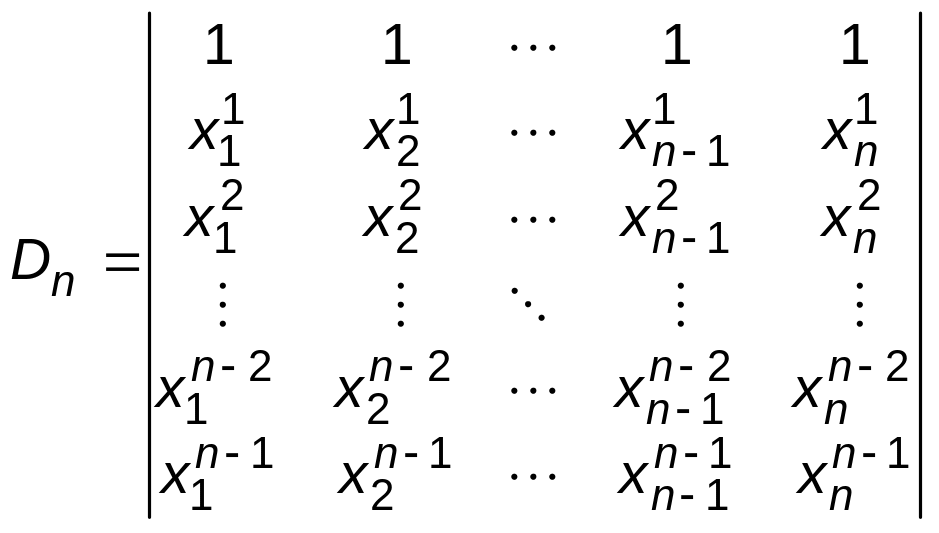
Віднімемо від останньої стрічки передостанню стрічку, помножену на і отримаємо:

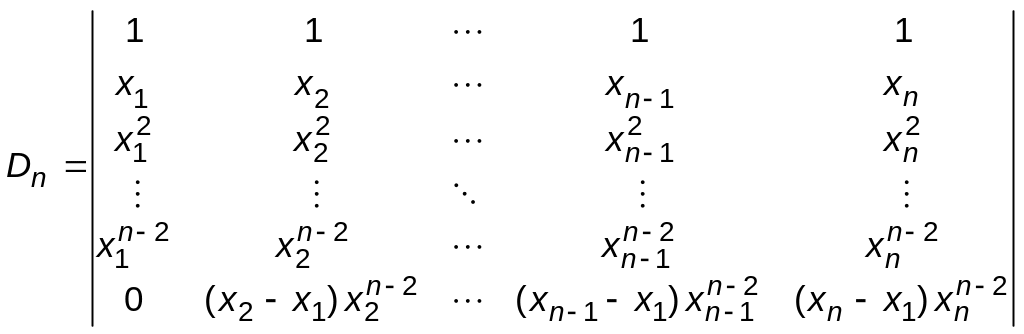
Після чого віднімемо від передостанньої стрічки третю знизу стрічку, домножену на , і т. д. Останній крок – від другої стрічки віднімаємо першу, домножаючи на . В результаті будемо мати:

=

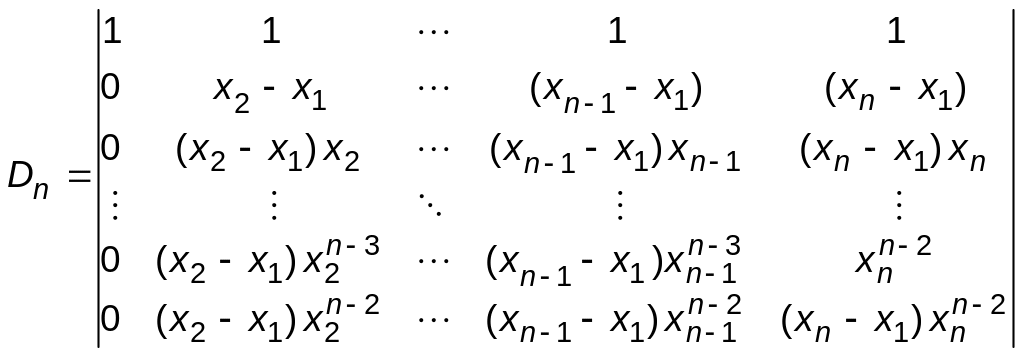= розкриваємо за 1-им стовпчиком =

= =

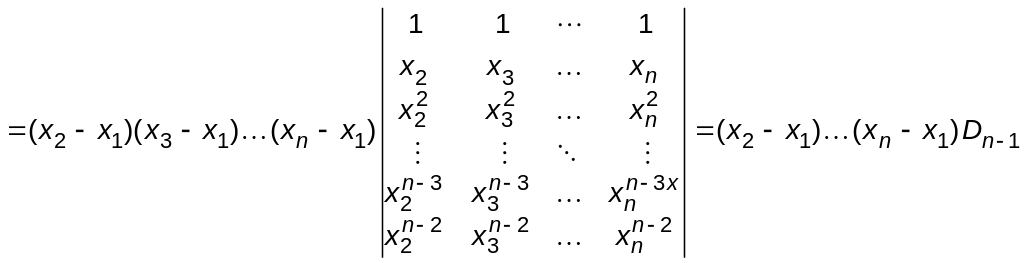
Розкриваючи визначник аналогічно, знаходимо: , отже

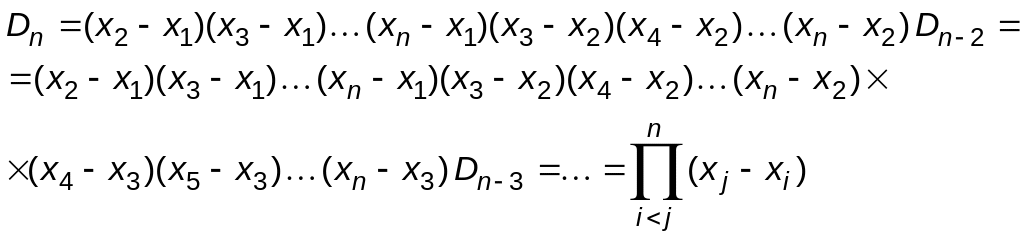
· Метод представлення визначника у вигляді суми визначників

Деякі визначники легко обчислюються шляхом розкладу їх в суму визначників того ж порядку відносно стрічок (або стовпчиків).