ЗМІСТ

Частина 1. Матриці 5

§ 1. Основні поняття та визначення. Лінійні операції над матрицями. Матриці-стовпчики і матриці-стрічки. Транспонування матриць 5

§ 2. Детермінант матриці 11

§ 3. Методи обчислення детермінантів матриць 17

§ 4. Мінори. Мінори довільного порядку. Ранг матриці 24

§ 5. Множення матриць 28

§ 6. Елементарні перетворення як множення матриць. Детермінант добутку 31

§ 7. Система лінійних алгебраїчних рівнянь 33

§ 8. Загальна теорія лінійних систем 36

§ 9. Критерій Фредгольма 37

§ 10. Знаходження розв’язків СЛАР 39

§ 11. Множина розв’язків однорідної системи. Загальний розв’язок системи лінійних рівнянь 39

Частина 2. Векторні простори 45

§ 12. Вступні зауваження 45

§ 13. Поняття вектора, означення векторного простору 47

§ 14. Приклади векторних просторів 48

§ 15. Найважливіші наслідки з означення векторного простору 50

§ 16. Лінійно залежні та лінійно незалежні вектори 51

§ 17. Приклади лінійно залежних та лінійно незалежних векторів 52

§ 18. Властивості лінійно залежних та лінійно незалежних векторів 52

§ 19. Вимірність векторного простору 53

§ 20. Базис у скінченновимірному векторному просторі 55

§ 21. Координати вектора 56

§ 22. Основні властивості координат вектора 57

§ 23. Заміна базису 58

§ 24. Приклади застосування методу координат у фізиці 60

Частина 3. Векторні простори зі скалярними добутками 64

§ 25. Скалярний добуток геометричних векторів 64

§ 26. Простір Евкліда 66

§ 27. Ортонормовані системи векторів 69

§ 28. Матриця Грама 71

§ 29. Лінійна залежність та незалежність векторів у просторі Евкліда 75

§ 30. Взаємні базиси 76

§ 31. Унітарний простір 82

Частина 4. Векторний добуток векторів та пов'язані з ним добутки 86

§ 32. Векторний добуток геометричних векторів 86

§ 33. Мішаний добуток та подвійний векторний добуток геометричних векторів 88

§ 34. Добутки векторів у тривимірному просторі Евкліда 92

§ 35. Обчислення мішаних і векторних добутків векторів, заданих у довільних базисах 95

§ 36. Символи Леві – Чивіта. 99

Частина 5. Системи координат, векторна алгебра в криволінійних координатах 103

§ 37. Загальна декартова система координат 103

§ 38. Спеціальні системи координат 107

§ 39. Локальні базиси криволінійних систем координат 112

§ 40. Фізичний базис та фізичні координати векторів 117

§ 41. Ортогональні криволінійні системи координат 119

§ 42. Довідкові формули для спеціальних систем координат 121

§ 43. Обчислення добутків векторів у криволінійних системах координат 122

Додаток 1. Пояснення деяких символів та символічних записів 123

Додаток 2. Уявлення про афінний простір 124

Література 128

Частина 1

МАТРИЦІ

§ 1. Основні поняття та визначення. Лінійні операції над матрицями. Матриці-стовпчики і матриці-стрічки. Транспонування матриць.

Основні поняття та визначення.

1.1. Означення. Матрицею розмірів , (тут ) назвемо сукупність виразів, розташованих у вигляді таблиці з m стрічок та n стовпчиків.

=

Вирази, які складають матрицю, називаються елементами матриці. В загальному випадку елементи матриці можуть мати довільну природу – це можуть бути дійсні або комплексні числа, символи, функції і т.д.

Якщо число стрічок в матриці дорівнює числу стовпчиків, то матриця називається квадратною, а число стрічок – порядком матриці. Інші матриці носять назву прямокутних. Матриці складаються з m стрічок та n стовпчиків, тому їх часто називають матрицями. Для матриці можна використовувати коротке позначення , а якщо розміри матриці обумовлено завчасно, то не вказуючи їх, будемо писати або . Елементи матриці позначають буквами з двома індексами: aⁱ_j або a_{i j}, Якщо два індекси розташовані внизу, то перший з них означає номер стрічки, а другий – номер стовпчика, на перетині яких розташований даний елемент матриці. Якщо ж один з індексів розташовано вверху, то тоді цей індекс означає номер стрічки, а нижній – номер стовпчика (не плутати верхні індекси з показниками степені!).

1.2. Зауваження. Для матриць, ялементами яких є дійсні або комплексні числа (числові матриці) справедливим є і таке означення – розглянемо дві множини цілих чисел: та Через позначимо множину всіх пар чисел виду , де – число з множини I, j - число з множини J. Матрицею називається функція на множині , тобто закон, який співставляє кожній парі деяке число .

1.3. Означення. Дві матриці і називають рівними, якщо вони мають одинакові розміри (кількість стовпчиків і стрічок матриць співпадають) і їх елементи, які стоять на однакових місцях, є рівними: .

1.4. Означення. Нехай і – матриці, які складаються з m стрічок і n стовпчиків. Сумою матриць і називають матрицю тих же розмірів , кожен елемент якої дорівнює сумі елементів матриць та , які стоять на тих же місцях, тобто елементи матриці пов’язані з елементами та матриць та рівністю

для всіх ; .

Суму матриць та позначають .

1.5. Зауваження. Операція “сума матриць” визначена тільки для матриць одних і тих же розмірів!

1.6. Означення. Матриця , елементи якої дорівнюють добутку елементів матриці на дійсне або комплексне число α називається добутком матриці на число α і позначається . Маємо

для всіх ; .

З означень 1.3. і 1.4. витікають наступні властивості операцій додавання матриць і одних і тих же розмірів та множення матриці на довільні числа α і β.

1.7. Властивість. Додавання матриць є комутативною операцією, тобто .

1.8. Властивість. Додавання матриць є асоціативною операцією:

.

1.9. Властивість. Множення матриці на число є дистрибутивною операцією по відношенню до додавання чисел:

1.10. Властивість. Множення матриці на число є дистрибутивною операцією по відношенню до додавання матриць:

1.11. Властивість. Множення матриці на число – асоціативна операція:

1.12. Означення. Матриця, всі елементи якої дорівнюють нулю, називається нульовою матрицею. Якщо – нульова матриця розмірів , то для любої матриці тих же розмірів маємо .

1.13. Означення. Матрицю (-1) називають протилежною до матриці і позначаємо . Матриця, протилежна до заданої матриці, має властивість

1.14. Означення. Операція віднімання матриць визначається через операції додавання матриць та множення матриці на число, тобто сума матриць і називається різницею матриць та і позначається

1.15. Означення. Квадратна матриця довільного порядку n всі “n” елементи якої розташовані на головній діагоналі і дорівнюють 1, а всі інші елементи дорівнюють нулю, називається одиничною і позначається .

1.16. Означення. Матрицю розмірів , тобто таку, яка складається з однієї стрічки, називають матрицею-стрічною або вектор-стрічкою або просто стрічкою довжини n. Матрицю розмірів , яка складається з одного стовпчика, називають матрицею-стовпчиком або вектор-стовпчиком висоти m або просто стовпчиком.

В подальшому зручно застосовувати позначення векторів-стовпчиків і векторів-стрічок, уперше запропоновані Полем Діраком. Зручність цих позначень полягає в тому, що вектор-стовпчик важко переплутати з вектор-стрічкою , а добуток матриць , що є числом, з добутком _, який є матрицею порядку n (операцію множення матриць буде означено пізніше) Позначення Дірака широко застосовуються в сучасній літературі з квантової механіки, квантової теорії поля, квантової оптики, фізики твердого тіла тощо.

Матрицю = довільних розмірів можна розглядати як сукупність стовпчиків висоти m або сукупність стрічок довжини n. Нехай , тоді матрицю можна записати у такому вигляді . Аналогічно, якщо

,

тоді та ж матриця запишеться у такому вигляді = .

1.17. Зауваження. Операцію додавання векторів-стрічок визначено для векторів-стрічок однієї довжини, так само як додавання векторів-стовпчиків – тільки для векторів-стовпчиків однієї висоти. Для цих двох видів матриць ми детальніше вивчимо операції додавання і множення на число. При цьому мова буде йти тільки про вектори-стовпчики, так як для векторів-стрічок всі властивості формуються і доводяться аналогічно.

1.18. Означення. Вектор-стовпчик називається лінійною комбінацією стовпчиків однакової висоти, якщо при деяких числах α₁ , …, α_m або більш детально

Числа називають коефіцієнтами лінійної комбінації. В силу означень операцій множення матриці на число та додавання ця рівність рівносильна числовим рівностям

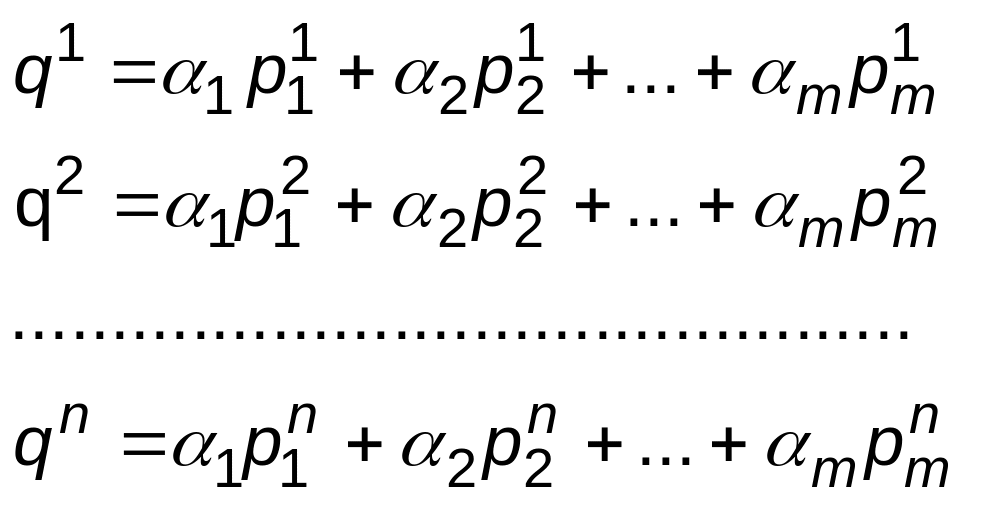
1.19. Означення. Вектор-стовпчик, всі елементи якого дорівнюють нулеві, називається нульовим і позначається наступним чином . Аналогічно визначається і нульова вектор-стрічка

1.20. Означення. Система з s стовпчиків однієї і тієї ж висоти називається лінійно незалежною, якщо з рівності

слідує . В противному випадку система з s стовпчиків є лінійно залежною.

1.21. Означення. Лінійну комбінацію вектор-стовпчиків, всі s коефіцієнтів якої дорівнюють нулеві, називають тривіальною. З допомогою цього терміну означення 1.20. можна сформулювати так: система стовпчиків є лінійно залежною, якщо існує рівна нульовому стовпчику нетривіальна лінійна комбінація цих стовпчиків. Система стовпчиків є лінійно незалежною тоді і тільки тоді, коли тільки тривіальна лінійна комбінація цих стовпчиків дорівнює нульовому стовпчику.

1.22. Приклад. Лінійно незалежною системою вектор-стовпчиків є наступна система з n вектор-стовпчиків:

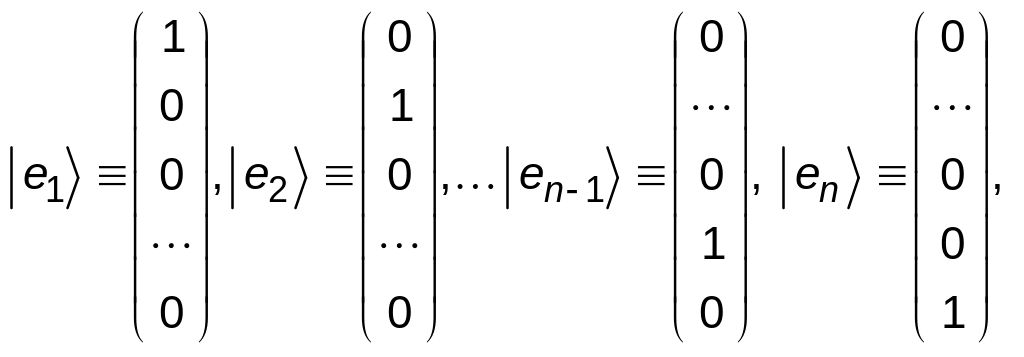
1.23. Властивість. Система з s > 1 стовпчиків лінійно залежна тоді і тільки тоді, коли хоча б один з стовпчиків є лінійною комбінацією інших стовпчиків.

Нехай система є лінійно залежною. Тоді, згідно означенню 1.20., існує нетривіальна лінійна комбінація системи векторів-стовпчиків, що розглядаються, рівна нульовому вектор-стовпчику:

Нехай який-небудь з коефіцієнтів Звідси

тобто j-тий стовпчик є лінійною комбінацією інших стовпчиків. Навпаки, якщо один з стовпчиків є лінійною комбінацією інших, тобто має місце рівність то з цієї рівності слідує існування нетривіальної лінійної комбінації векторів з відмінними від нуля коефіцієнтами, рівної нульовому вектору

1.24. Властивість. Якщо система векторів утримує нульовий вектор стовпчик, то система є лінійно залежною.

Дійсно, любий нульовий стовпчик є тривіальна лінійна комбінація довільної системи вектор-стовпчиків, тобто доведення цієї властивості зводиться до доведення попередньої властивості.

1.25. Властивість. Якщо деякі з стовпчиків даної системи утворюють самі по собі лінійно залежну підсистему стовпчиків, то і вся система є лінійно залежною.

В силу сформульованого, існує нетривіальна лінійна комбінація деякої підсистеми заданої системи стовпчиків, рівна нульовому стовпчику. Якщо до цієї комбінації стовпчиків додати інші стовпчики заданої системи з нульовими коефіцієнтами, то отримаємо нетривіальну лінійну комбінацію всіх стовпчиків, яка дорівнює нульовому стовпчику.

1.26. Властивість. Любі стовпчики, які входять в лінійно незалежну систему стовпчиків, самі по собі утворюють лінійно незалежну систему.

Якби було не так, то ми прийшли б до протиріччя з попередньою властивістю.

1.27. Властивість. Якщо стовпчик є лінійна комбінація стовпчиків , які є підсистемою деякої системи стовпиків , то є також лінійною комбінацією цієї системи стовпчиків.

Для доведення до даної лінійної комбінації підсистеми достатньо добавити ті стовпчики системи стовпчиків, яких не вистачає, з нульовими коефіцієнтами.

1.28. Властивість. Любий стовпчик висоти n є лінійною комбінацією стовпчиків

Дійсно, яким би не був стовпчик , лінійна комбінація стовпчиків з коефіцієнтами, які співпадають з відповідними елементами заданої матриці, дорівнює заданій матриці :

.

Розглянемо матрицю з m стрічок та n стовпчиків. Їй можна співставити матрицю з n стрічок та m стовпчиків за наступним правилом: елементи кожньої стрічки матриці записуються в тому ж порядку в стовпчики матриці , причому номер стовпчика співпадає є номером стрічки, тобто -та стрічка матриці складається з тих же елементів і в тому ж порядку, що й -ий стовпчик матриці

.

Таку матрицю називають транспонованою по відношенню до і позначають , перехід від до називають транспонуванням. Визначення транспонованої матриці можна записати у вигляді рівностей: , , ,..., ,..., , які зв’язують елементи матриці і для всіх , .

1.29. Приклад. Матриці , і називається матрицями Паулі і відіграють надзвичайно важливу роль в квантовій механіці і квантовій теорії поля.

Для цих матриць маємо

, і .

Очевидно, , і .

1.30. Означення. Матриці, для яких справедливо , називаються симетричними, а матриці для яких , називаються антисиметричними. Матриці і є симетричними, а матриця є антисиметричною.

§ 2. Детермінант матриці

1.31. Зауваження. Поняття «Детермінант» («Визначник») означено тільки для квадратних матриць. Детермінінт матриці позначається , або, якщо потрібно виписати елементи цієї матриці – прямими рисками по боках цієї матриці.

1.32. Означення. Детермінант квадратної матриці – це число або символ, які їй ставляться у відповідність і можуть бути знайдені за елементами матриці згідно наступним означенням:

1. Детермінантом матриці порядку 1 називається єдиний елемент цієї ж матриці

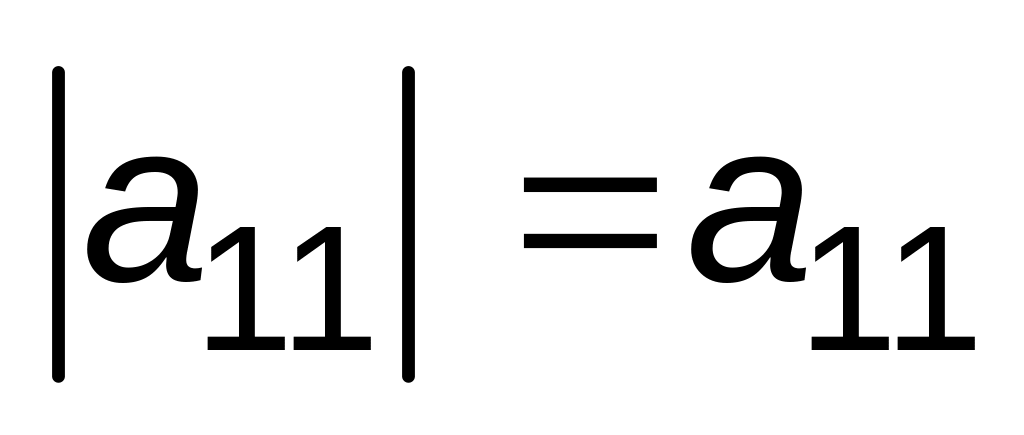
2. Детермінант матриці порядку n > 1 називається число або символ, які наступним чином визначаються через елементи матриці

де детермінант матриці порядку ( ), яка отримується з матриці А викреслюванням її першої стрічки і k-го стовпчика.

називається додатковим мінором елемента заданої квадратної матриці. По аналогії можна визначити додатковий мінор довільного елемента як детермінант матриці порядку ( ), яка отримана з початкової матриці А викреслюванням тієї ж стрічки і того ж стовпчика, в яких розташовано елемент , тобто –ої стрічки та -го стовпчика.

1.33. Приклад. Користуючись означенням 1.32 знайдемо визначник матриць Паулі:

Властивості детермінантів

1.34. Властивість. Для кожної матриці А порядку n має місце формула

,

яка називається розкладом детермінанта за першим стовпчиком.

Для доведення скористаємось методом математичної індукції.

Розглянемо визначник матриці другого порядку:

.

Вважаючи, що наступна рівність , де А – матриця порядку ( ), є справедливою, отримаємо з неї основне співвідношення. Розкладемо визначник матриці порядку n за першою стрічкою, виділивши в сумі явно перший член:

При любому матриця, яка отримується з матриці А порядку n викреслюванням першої стрічки і k–ого стовпчика, утримує перший стовпчик без елемента матриці А. Розкладемо по цьому стовпчику, врахувавши, що i-та стрічка матриці А в входить під номером ( ), так як в не ввійшла перша стрічка матриці А.

Тому при отримаємо де – детермінант матриці порядку , яка отримується з викреслюванням її -ої стрічки та 1-го стовпчика, або, що те ж саме, викресленням з матриці n-ого порядку 1-ої і і-ої стрічок та 1-го і k–го стовпчиків.

Тоді

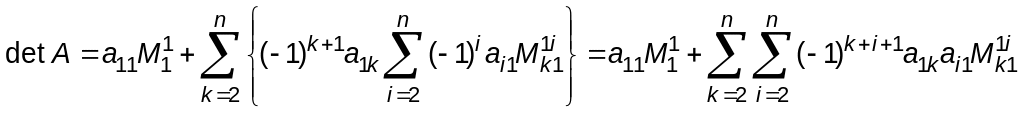
Змінимо порядок сумування і винесемо множник, не залежний від k, за внутрішній знак суми.

Врахуємо, що в силу того, що в матриці, детермінантом якої є , в порівнянні з матрицею А пропущено перший стовпчик і всі номери стовпчиків зменшені на 1. Таким чином, маємо

=

1.35. Властивість. Для любої квадратної матриці .

Скористаємось знову методом математичної індукції. Для матриць другого порядку маємо:

,

.

Вважаємо, що . Тоді, використовуючи означення 1.36. для знаходження визначника матриці та властивість 1.34. для знаходження визначника транспонованої матриці , запишемо

,

де - елементи першого стовпчика транспонованої матриці, тобто . Враховуючи, що , приходимо до рівності .

1.37. Наслідок. З властивості 1.35. витікає рівноправність стрічок і стовпчиків – якщо справедливе яке-небудь твердження про детермінанти, яке має відношення до стрічок відповідної матриці, то є справедливим і аналогічне твердження, яке стосується стовпчиків. В силу цього наступні властивості достатньо довести тільки для стрічок.

1.38. Властивість. Якщо в квадратній матриці поміняти місцями які-небудь дві стрічки (два стовпчики), то детермінант матриці поміняє знак, не змінившись за абсолютніою величиною.

Використовуємо для доведення метод математичної індукції

.

Припустимо, що твердження справедливе для матриць порядку ( ) і доведено його для матриць порядку n. Нехай номера стрічок, які ми переставляємо і . Напишемо розклад визначника за першим стовпчиком, виділивши в ньому дві складові, які відповідають стрічкам, що переставляються

.

Аналогічно для матриці В, яка отримується з матриці А перестановкою k–ої і стрічок

.

При , в і входять і стрічки, але в різному порядку, а інші їх стрічки однакові, отже згідно припущенню індукції при , . Матриці, детермінанти яких позначено і співпадають – вони отримані викреслюванням стрічки з матриці В або, що те ж саме, k-ої стрічки матриці А. Тому = . Аналогічно .

Таким чином, порівнюючи і бачимо, що вони рівні за абсолютною величиною і відрізняються знаком. Нехай тепер в матриці А порядку n переставлено стрічки з номером і та j ( ). Перестановку і-ої та j-ої стрічок можна провести, переставляючи тільки сусідні стрічки: спочатку j–ту стрічку переставляємо послідовно з стрічками, які стоять над нею (остання буде і-та), потім і-у стрічку переставляємо на j-те місце міняючи місцем з стрічками, розташованими нижче від неї. Всього буде зроблено непарну кількість перестановок сусідніх стрічок. Так як при кожній з перестановок детермінант змінює знак, то в результаті знак детермінанту зміниться.

Властивість 1.37. називають антисиметрією детермінанту відносно перестановок стрічок (стовпчиків).

Використовучи властивість антисиметрії можемо довести наступне.

1.39. Властивість. Для кожної квадратної матриці А порядку n при довільному і ( ) має місце співвідношення

і при довільному j ( )

Очевидно, при перше співвідношення є означенням детермінанту.

Доведемо це співвідношення при . Для цього переставимо і-ту стрічку на перше місце так, щоб не порушувати порядок інших стрічок, переставляючи і–ту стрічку послідовно з усіма стрічками, розташованими вище неї. Вище і-ої стрічки знаходиться стрічка, Тому, якщо В – матриця, отримана з матриці після перестановки -ої стрічки на місце першої, то .

Розкладемо по першій стрічці (і-ій стрічці матриці А)

,

де – визначник матриці, яка отримується з матриці В викреслюванням першої стрічки і k-ого стовпчика, або, що те ж саме – з матриці А викреслюванням і-ої стрічки і k–ого стовпчика. Тому . Враховуючи, що , отримаємо .

1.40. Властивість. Якщо і-ий стовпчик (стрічка) матриці А є лінійна комбінація стовпчиків (стрічок) та , тобто має вигляд де і – довільні числа, то , де матриці і отримуються з матриці А заміною її і-го стовпчика відповідно на стовпчики і .

Ця властивість носить назву лінійності детермінанта по стовпчику (стрічці).

Дійсно, розкладемо визначник за і-тим стовпчиком і врахуємо :

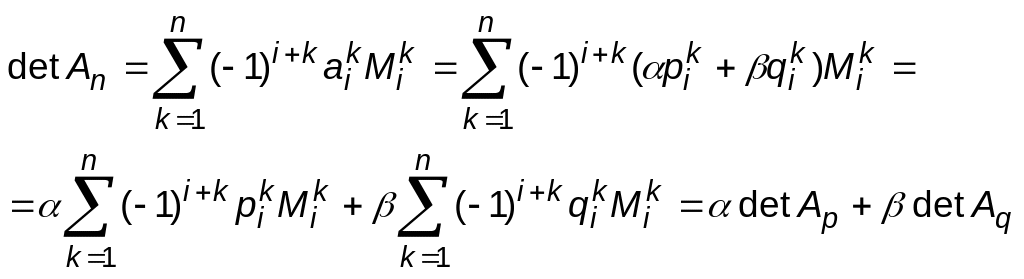
1.41. Зауваження. Цю властивість лінійності детермінанту по стовпчику можна сформулювати у вигляді двох окремих властивостей.

1). При множенні стовпчика матриці на число її детермінант множиться на це число.

2). Якщо стовпчик матриці є сумою двох стовпчиків, то її детермінант є сума детермінантів відповідних матриць.

1.42. Властивість. Якщо в матриці А стовпчики (стрічки) лінійно залежні, то її визначник дорівнює нулю.

В першу чергу зауважимо, що якщо в матрицю входить нульовий рядок або нульовий стовпчик, то її визначник очевидно є рівним нулю. Крім цього, з властивості антисиметрії визначника слідує, що якщо матриця утримує два ідентичних рядки або стовпчики, то її визначник також дорівнює нулю. Якщо рядки в заданій матриці є лінійно залежними, то це означає, що хоча б один рядок (нехай його номер є ) матриці є лінійною комбінацією інших рядків цієї матриці, тобто є справедливою наступна рівність:

.

Тоді, розкладаючи визначник цієї матриці за і-тим рядочком і використовуючи властивість 1.39., отримуємо

де – матриця, в якій на місці і-ого рядка знаходиться будь-який k-тий рядок цієї матриці, який не співпадає з і-тим рядком. Отже, кожна матриця утримує дві ідентичні стрічки, тому визначник кожної з цих матриць дорівнює нулю, тобто