· Мають місце наступні теореми про базисний мінор

1.55. Теорема. В довільній матриці кожен стовпчик є лінійною комбінацією базисних стовпчиків, а кожна стрічка – лінійною комбінацією базисних стрічок.

Для доведення достатньо згадати метод Гауса приведення матриці до спрощеного вигляду – до небазисних стрічок додавались базисні і в результаті отримували нульову стрічку.

1.56. Наслідок. Якщо А – квадратна матриця і , то хоча б один з стовпчиків є лінійною комбінацією інших стовпчиків, а одна з стрічок – лінійна комбінація інших стрічок.

1.57. Теорема. Ранг матриці А дорівнює максимальному числу лінійно незалежних стовпчиків цієї матриці.

Якщо , то всі стовпчики є нульові і немає ні одного лінійно незалежного стовпчика. Нехай . Покажемо, що в А існує r лінійно незалежних стовпчиків. Дійсно, розглянемо складену з елементів матриці А матрицю порядку r, детермінантом якої є базисний мінор. Стовпчики представляють собою частини стовпчиків А. Якби стовпчики в А, в яких розташований базисний мінор, були лінійно залежні, то були б лінійно залежні і стовпчики і базисний мінор дорівнював би нулю.

Доведемо, що любі р стовпчиків матриці А лінійно залежні, якщо . Складемо матрицю В з цих р стовпчиків. Очевидно, що , тобто кожен мінор матриці В є мінором матриці А, отже , a . Так як , то хоча б один із стовпчиків матриці В не входить в базисний мінор, а отже є залежним. Аналогічно доводиться, що ранг матриці дорівнює максимальному числу лінійно незалежних стрічок.

Очевидно, що ранг матриці не змінюється при її транспонуванні.

1.58. Приклад. Знайти ранг матриці

.

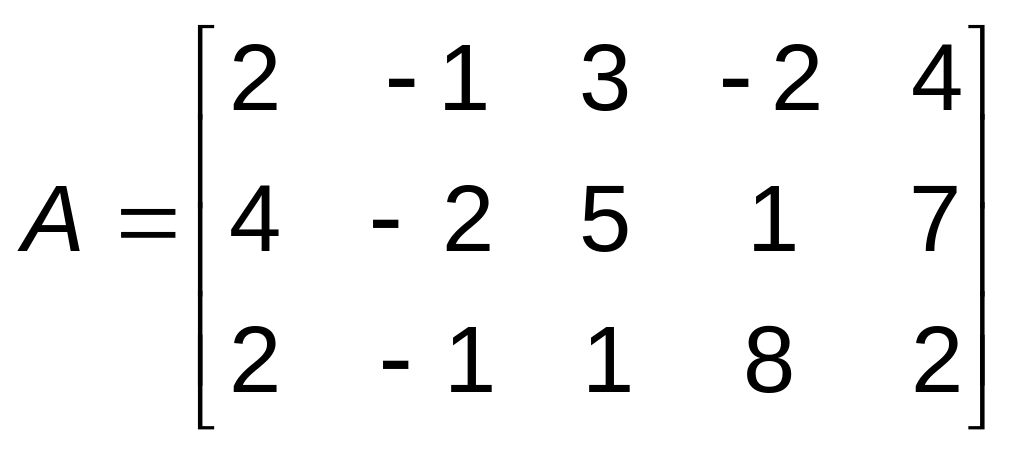Скористаємося тим, що елементарні перетворення не змінюють ранг матриці. Крок 1 – до 2-ої і 3-ої стрічок додаємо 1 стрічку, помножену відповідно на і . Отримаємо

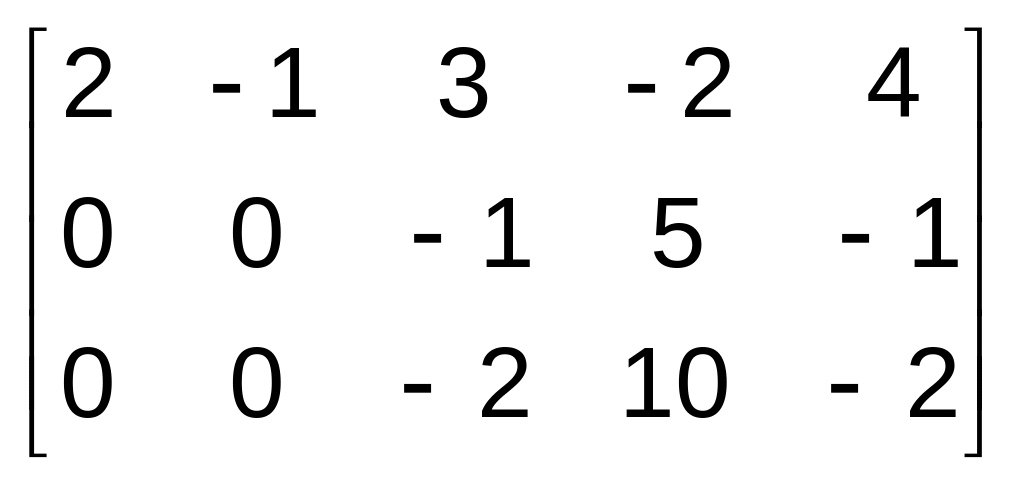
Аналізуємо частину отриманої матриці, яка знаходиться нижче 1-ої стрічки і правіше 1-го стовпчика. Відмінний від нуля елемент знаходиться на перетині 2-ої стрічки і 3-го стовпчика, тому крок 2 – до 3-ої стрічки додаємо 2-гу стрічку, домножену на і отримуємо

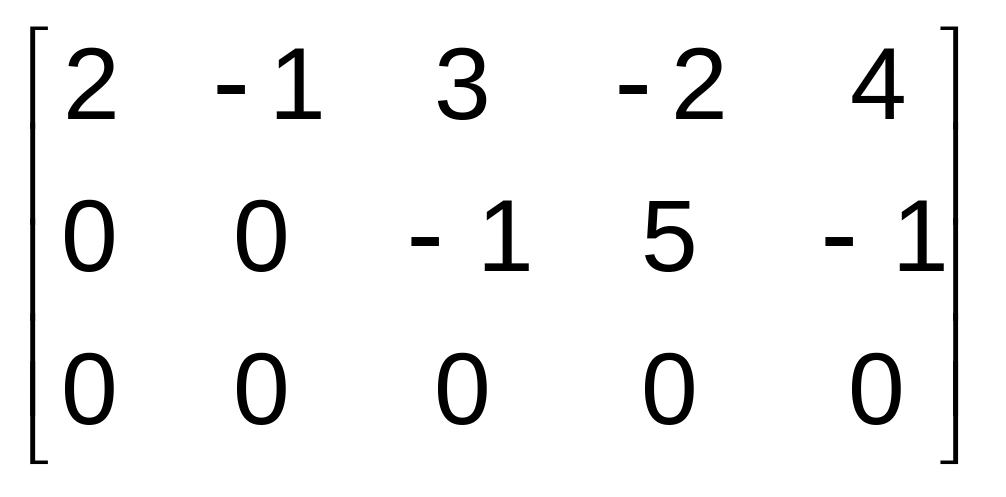
Оскільки в отриманій матриці нижче другої стрічки і правіше третього стовпчика відмінних від нуля елементів немає, то .

§ 5 Множення матриць. · Властивості множення матриць.

Операція множення матриць означена тільки для такої впорядкованої пари матриць, в якій кількість стовпчиків першої матриці збігається з кількістю стрічок другої матриці.

1.59. Означення. Добутком матриці розмірів на матрицю розмірів називається матриця розмірів елементи якої пов’язані з елементами та матриць та наступним чином:

, де ; .

1.60. Приклад. Нехай дана матрична-стрічка довжини , а саме і матричний стовпчик 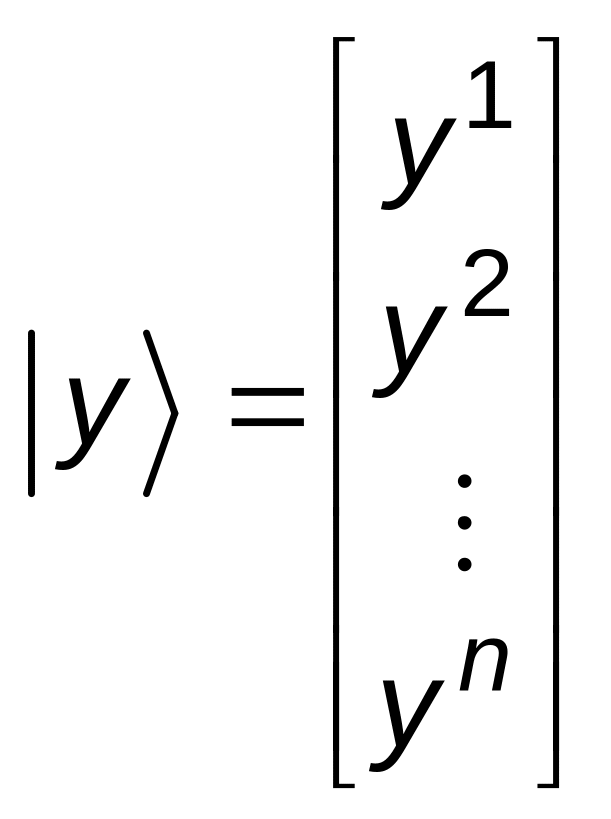висоти . Добуток є матриця розміром , єдиний елемент якої згідно з означення операції множення матриць визначається як: . Добуток є матриця розмірів елементами якої є всеможливі добутки , де .

Означення операції множення матриць дозволяє ввести для будь-якої квадратної матриці операцію піднесення до степеню , тобто .

1.61. Приклад.

Очевидно

1.62. Припущення. -ий стовпчик матриці є лінійною комбінацією стовпчиків матриці з коефіцієнтами, рівними елементам -ого стовпчика матриці .

Нехай матриця має розміри , а матриця – , тоді матриця матиме розмір . Запишемо як матрицю-стрічку елементами якої є її стовпчики . Тоді матрицю можна також записати як матрицю-стрічку, стовпчики якої визначаються так:

=

.

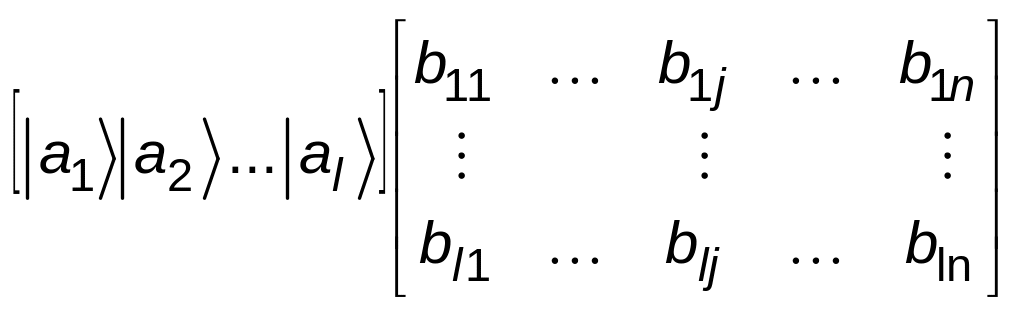Звідки слідує, що -ий стовпчик матриці є .

1.63. Припущення. -та стрічка матриці є лінійна комбінація стрічок матриці з коефіцієнтами, рівними елементам -ої стрічки матриці .

Записуючи матриці і у вигляді матриць-стовпчиків висоти і доводимо аналогічно попередньому.

1.64. Властивість. Множення матриць не комутативно, тобто в загальному , наприклад перемножимо матриці Паулі:

Різницю називають комутатором матриць та і позначають . Суму називають антикомутатором і позначають . Очевидно

.

Безпосередньо множенням матриць можна переконатись, що

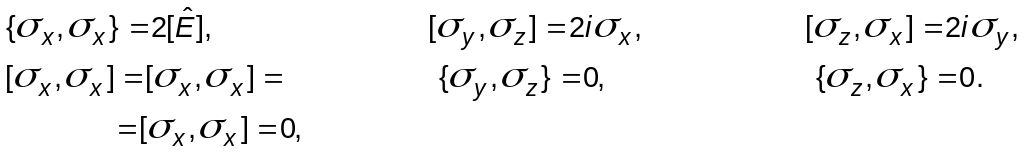
За допомогою символу Леві-Чевіта комутативні співвідношення можна записати таким чином , де , а за допомогою символу кронекера всі антикомутаційні співвідношення записуються так

.

Якщо які-небудь матриці А та В задовільняють співвідношенню А В = В А, то такі матриці називають перестановочними. Одинична матриця порядку n є перестановочною з любою квадратною матрицею того ж порядку, тобто . Які б не були А та В, якщо О – нульова матриця, то , .

1.65. Властивість. Множення матриць асоціативно, тобто якщо визначені добутки АВ і (АВ)С, то визначені добутки ВС і А(ВС), і виконується рівність (АВ)С = А(ВС).

Нехай матриці А, В, С мають розміри , i відповідно. Якщо добуток АВ визначено, то і добуток АВ має розміри , тому якщо визначено добуток (АВ)С, то . Матриця АВ складається з елементів

( ; ),

.

Але, оскільки , то визначено добуток матриць ВС, елементи якого

.

Оскільки висота стовпчика (кількість стрічок) матриці дорівнює , тобто довжинi стрічки матриці А, то визначено добуток А(ВС), елементи якого мають вигляд

.

1.66. Властивість. Множення матриць дистрибутивно по відношенню до додавання, тобто, якщо має зміст вираз , то .

Очевидно, що В і С мають одинакові розміри , А – розмір (р – довільне). Ця сума може бути представлена у вигляді

,

де ( , ).

1.67. Властивість. Якщо добуток АВ має зміст, то .

1.68. Властивість. Ранг добутку двох матриць не перевищує рангів співмножників.

Для доведення розглянемо матрицю D , складену з усіх стовпчиків матриць А та АВ. Запишемо її символічно . Очевидно, що Згідно припущення 1.61 стрічки АВ є лінійними комбінаціями стовпчиків А, тому , таким чином маємо . Аналогічно доводиться, що

1.69. Властивість. Якщо визначено добуток АВ, то визначено і добуток В^ТА^Т і виконується рівність (АВ)^Т = В^ТА^Т.

Нехай матриці А та В мають розміри і . В матриці АВ на перетині і-ої стрічки та j–го стовпчика знаходиться елемент , ( ). j-та стрічка матриці В^Т складається з елементів , а і-ий стовпчик матриці – з елементів , тому добуток визначений і в ньому на перетині j–ої стрічки і і-го стовпчика є елемент , що збігається з .

1.70. Наслідок. Якщо визначено добуток АВС, то , в силу .

1.71. Означення. Матриця , що з деякою заданою матрицею задовільняє рівності (де – одинична матриця деякого порядку ), називається оберненою для і позначається .

Так як і перестановочні, то вони обидві повинні бути квадратними того ж порядку . Так як , то матриця може мати обернену тільки тоді, коли її визначник відмінний від нуля.