1.47. Приклад.

Розкладемо відносно першої стрічки:

Кожен з визначників розкладаємо відносно другої стрічки:

= 0 + 0 + 0 + 0 так як в першому визначнику є дві пропорційні стрічки ( ), тому він дорівнює 0, четвертий визначник дорівнює 0 (очевидно), а другий і третій визначники зводяться до визначників типу 1 (з пропорційними стрічками) або типу 4. Отже, якщо → n > 2, то . Для випадків і маємо

· Метод заміни елементів визначника.

Нехай . Знайдемо

Очевидно, що складові, які утримують більше однієї стрічки елементів, рівних х, дорівнюють нулю. Складові, які утримують одну стрічку елементів, рівних х, розкладем за цією стрічкою:

,

де – алгебраїчні доповнення елементів визначника.

.

1.48. Приклад. Знайдемо

.

Віднімемо від усіх елементів визначника число х, тоді

Оскільки всі недіагональні алгебраїчні доповнення дорівнюють нулю, тому вклад дають лише діагональні:

В завершення доведемо так звану формулу повного розкладу визначника

де сума береться по всіх перестановках чисел 1, 2, ..., n, а є число порушень порядку в даній перестановці. Для випадку маємо

Вважаємо, що дане співвідношення є вірним для матриць порядку . Тоді розкладаючи визначник за 1-ою стрічкою, отримаємо

Враховуючи що – визначник матриці порядку , отриманий з матриці шляхом викреслювання першої стрічки і k-го стовпчика і, що в перестановці число k порушує порядок раз, можна стверджувати, що а також те, що парність співпадає з парністю маємо:

§ 4. Мінори. Мінори довільного порядку. Ранг матриці.

Нагадаємо, що число називається додатковим мінором довільного елементу квадратної матриці A і дорівнює детермінанту матриці , яка отримується з матриці А викреслюванням і-ої стрічки та j-го стовпчика.

Виберемо в необов’язково квадратній матриці s номерів стрічок і s номерів стовпчиків , причому будемо вважати, що ці номери розташовані в порядку зростання , .

1.49. Означення. Мінором порядку s матриці А називається детермінант матриці порядку s, утвореної елементами, розташованими на перетині вибраних стрічок і стовпчика, тобто

1.50. Зауваження. Якщо матриця квадратна, то кожному мінору можна співставити додатковий мінор – визначення матриці порядку , який отримується з А викреслюванням стрічок з номерами і стовпчиків , тобто тих, в яких розташований мінор . Має місце формула Лапласа для обчислення визначника матриці порядку n:

де сума береться по всіх можливих перестановках таким, що .

1.51. Означення. В матриці А розмірів мінор порядку r називається базисним, якщо він не дорівнює нулю, а всі мінори порядку ( ) дорівнюють нулю або мінорів порядку ( ) взагалі немає, тобто r співпадає з найменшим з чисел m та n.

В матриці може бути декілька базисних мінорів, але всі базисні мінори мають один і той же порядок. Стовпчики і стрічки, на перетині яких розташований базисний мінор, називаються базисними стовпчиками і стрічками.

1.52. Означення. Рангом матриці називається порядок базисного мінора, або самий великий порядок, для якого існують відмінні від нуля мінори. Якщо кожен елемент матриці дорівнює нулю, то ранг такої матриці дорівнює нулю.

1.53. Зауваження. Ранг матриці позначають . Ранг матриці – це число.

Найпростіше знаходити ранг матриці і її базисний мінор за допомогою елементарних перетворень.

1.54. Припущення. Елементарні перетворення не змінюють рангу матриці.

Дійсно,

а) При множенні стрічки на число λ ≠ 0 базисний мінор або не зміниться або помножиться на λ. Ні один мінор, рівний нулю, не стане відмінним від нуля .

б) Якщо всі мінори порядку ( ) дорівнюють нулю, то додавання стрічок не зробить ні один з них відмінним від нуля (на основі властивостей детермінантів).

в) При перестановці стрічок мінор може змінити знак або може змінитись на мінор, який не більше ніж знаком відрізняється від іншого мінора тієї ж матриці або взагалі не зміниться.

На практиці ранг матриці знаходять методом приведення матриці до спрощеного вигляду.

Нехай дано матрицю А розмірів . Нехай – номер першого стовпчика, який утримує ненульові елементи. Якщо такого стовпчика немає, тоді базисного мінора немає, а отже . Нехай – ненульовий елемент -го стовпчика. Переставимо -ту стрічку на перше місце і розділимо її на , а елементарними перетвореннями всі інші елементи -го стовпчика перетворимо в нуль

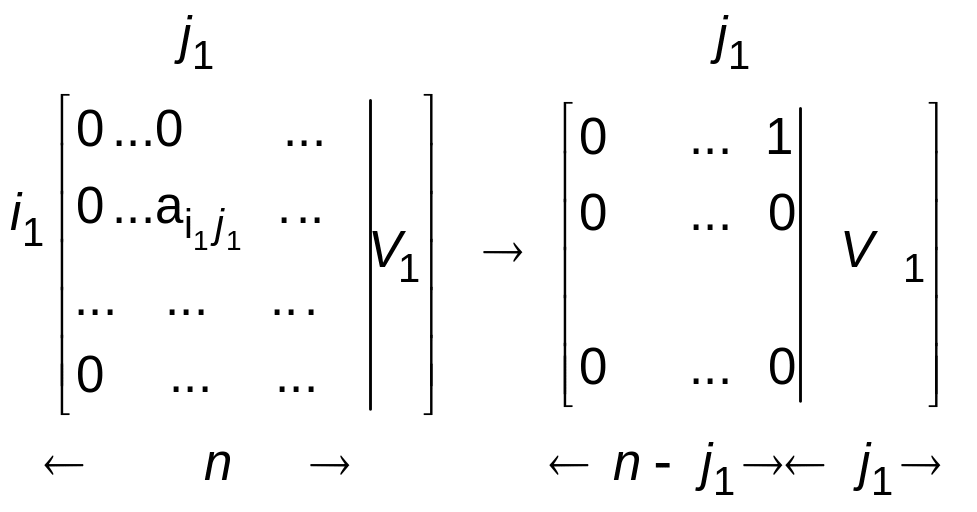
Тут V₁ – матриця розмірів .

Може виявитись, що останні стрічок матриці А нульові, тоді перетворення завершені і . В протилежному випадку, нехай – номер самого лівого стовпчика, який утримує ненульовий елемент в останніх стрічках. Переставимо ці стрічки таким чином, щоб стрічка, яка утримує цей елемент, стала другою і розділимо її на цей елемент. Елементарними перетвореннями перетворимо в нуль всі інші елементи j₂–стовпчика. При цьому стовпчиків матриці А не зміняться. V₂ – матриця розмірів ; символом “ ” позначено елементи, про які нічого не можна сказати.

Матриця матиме наступний вигляд:

Якщо в останніх стрічках є ненульові елементи, то продовжуємо ті ж перетворення і т.д. до тих пір, поки останні стрічок матриці будуть складлатись з нулів або ж не будуть вичерпані всі стрічки.

Таким чином за допомогою елементарних перетворень стовпчиків кожну матрицю розмірів можна привести до наступного вигляду - деякі r стовпчиків співпадають з першими r стовпчиками одиничної матриці порядку m. Якщо , то останні стрічок складаються з нулів. Матриці такого виду називають спрощеними. Мінор спрощеної матриці, розташований в перших r стрічках і стовпчиках дорівнює 1, ненульових мінорів більшого порядку немає, отже цей мінор є базисним, а ранг спрощеної матриці дорівнює r. Якщо ми привели матрицю А до спрощеного вигляду і отримали матрицю рангу r, то й ранг матриці А також був r. Приведену процедуру знаходження рангу називають методом Гауса.

Розглянемо квадратну матрицю з відмінним від нуля визначником ( ). У неї всі стовпчики базисні отже її спрощений вигляд – одинична матриця, тобто кожну квадратну матрицю з ненульовим визначником можна перетворити в одиничну матрицю.

Очевидно, що якщо А – матриця розмірів , то який би не був базисний мінор цієї матриці, при допомозі елементарних перетворень стрічок матриці А ми можемо перетворити базисні стовпчики в стовпчики одиничної матриці. Якщо , то останні стрічок будуть нульові.