
§ 3. Класифікація функцій

Явно задана функція , якщо вона задана формулою y= f(x) в якій права частина не містить залежної змінної (кажуть, що така функція розв’язана відносно залежної змінної). Наприклад: y = x2 + 5x + 1
Неявно задана функція, якщо вона задана формулою F(x;y) = 0 не розв’язаною відносно залежної змінної. Наприклад: x2 + y2 = R2
Параметрично
задана функція , якщо
і змінна х і змінна у виражені через
проміжну змінну ( параметр)
t :
![]() ;
;
Елементарні функції – функції визначені формулами, що містять скінчене число операцій: додавання, множення, ділення, піднесення до степеня, обчислення логарифмів, обчислення тригонометричних функцій (тобто це сукупність всіх алгебраїчних, та трансцендентних функцій).
Прикладами неелементарних функцій є такі: y = |x| ,y = [x] ,y = {x}
Складна функція (функція від функції, композиція функцій).
Наприклад: y = lgsinx є композицією двох функцій u = g(x) = sin (x), та функції y = f(u) = lg(u) отже y = f(g(x)).
Обернена
функція. 

 Якщо
функція f відображає змінні х з області
визначення Х на змінні у з множини
значень у, то функцію g, що буде відображати
змінні у на змінні х називають функцією,
оберненою до функції f . Позначають g = f
-1 Наприклад,
якщо
Якщо
функція f відображає змінні х з області
визначення Х на змінні у з множини
значень у, то функцію g, що буде відображати
змінні у на змінні х називають функцією,
оберненою до функції f . Позначають g = f
-1 Наприклад,
якщо
y = 2x - 4 то, виразивши в цій залежності х через у :
х = 0,5у + 2 отримаємо обернену функцію до даної. Якщо ж використати традиційну домовленість, що незалежну змінну позначають буквою х а залежну змінну буквою у , то остаточно функцію g можна записати у виді: y = 0,5x + 2. Графіки взаємо обернених функцій симетричні відносно прямої y = x.
 y
y
4
2
0 2 х
y = x
Теорема про обернені функції: Для всякої неперервної зростаючої (спадної) функції у = f(x), що задана на відрізку а;b з множини значень f(а);f(b) існує однозначна зростаюча ( спадна) і неперервна обернена функція, що відображає відрізок f(а);f(b) на відрізок а;b x = g(y)
Б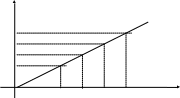 ільш
наочні відомості про функцію можна
отримати, якщо побудувати її графік.
проілюструємо це на функції , що задавалась
в §1.
як приклад табличним способом. В цьому
прикладі розглядалась функція доходу
від об`єму продажу. Використовуючи
наведену раніш таблицю, побудуємо графік
функції по точкам: (30;3000), (40;4000), (28;2800),
(14;1400), (36;3600).
ільш
наочні відомості про функцію можна
отримати, якщо побудувати її графік.
проілюструємо це на функції , що задавалась
в §1.
як приклад табличним способом. В цьому
прикладі розглядалась функція доходу
від об`єму продажу. Використовуючи
наведену раніш таблицю, побудуємо графік
функції по точкам: (30;3000), (40;4000), (28;2800),
(14;1400), (36;3600).
Доход
4000
3000
2000
1000
0 10 20 30 40 Об`єм продажу
Зауваження. Строго кажучи, графіком таблично заданої функції у наведеному прикладі буде п’ять точок, що лежать на одній прямій. Якщо вважати припустимим значенням об`єму продажу будь яке невід`ємне ціле число (тому як продукція рахується в штуках), то при сталій ціні одиниці продукції графіком доходу буде сукупність точок виду (n;100n), де n- об`єм продукції в штуках. Якщо б розглядалась продукція, що допускає (теоретично) безмежний поділ, наприклад добич нафти, газу і т. п., то кількість продукції можна б було представити будь яким невід`ємним числом в деякій системі одиниць вимірювання, наприклад літри, грами і т. п. Якщо 100 гр. од. - ціна одиниці об`єму газу, то вартість х одиниць об`єму буде дорівнювати 100х, тоді графік залежності доходу від об`єму продажу газу буде промінь, що зображений на малюнку.
При
побудові графіка функції можна
використовувати міліметровий папір
але зручніше це робити з використанням
комп`ютера, при цьому дуже важливо
правильно визначити “графічне вікно”
, яке зазвичай включає мінімальне
значення для х (x min )
та максимальне значення для х ( x max
), масштаб для х ( x
scale ),
а також масштаб для значень функції y
(y scale ).
Наприклад, якщо ми бажаємо побудувати
графік функції
![]() і будемо використовувати таке графічне
вікно:
і будемо використовувати таке графічне
вікно:
x min = -2; x max = 1; x scale = 1;
y min = -5; y max = 5; y scale = 1,
то на екрані дисплея ми зовсім не побачимо графіка функції, а тільки координатні осі. Це пов`язано з тим , що область визначення наведеної функції задається нерівністю х 2 Згадаємо, що вираз під знаком квадратного кореня не може бути від`ємним, і тому графік просто не попаде у вікно. Якщо ж ми змінимо графічне вікно на
x min = 0; x max = 9; x scale = 1;
y min = -1; y max = 3; y scale = 1,
то побачимо на дисплеї приблизно таке зображення як показано на малюнку
 У
У
3
0 2 9 X
Слід відмітити, що вибір зручного і правильного графічного вікна залежить від функції, яку ми бажаємо побудувати. Тільки знаходження області визначення функції та множини її значень може допомогти нам зробити правильний вибір відповідного вікна.
Зручною комп'ютерною програмою для побудови графіків функцій є "GRAN1"
Основні елементарні функції їх графіки, властивості та перетворення вивчаються в середній школі, тому нагадаємо довідковий матеріал:
Основні види функцій |
||
№ |
Функція |
Графік |
1 |
Стала функція y=b; b=const D(y)=(-;) E(y)=b |
y=b
|
2 |
Пряма пропорційність y=kx; k0 D(y) = (-;) E(y) = (-;) y = kx - непарна функція При k0 - функція зростає При к0 - функція спадаюча k = tg |
У y=kx
0 Х |
3 |
Лінійна функція y = kx+b; bR D(y) = (-;) При k0 - функція зростає При к0 - функція спадаюча k = tg |
b
|
4 |
Обернена пропорційність y =k/x; k0 D(y) = (-;0)(0;) E(y) = (-;0)(0;) При k0 – спадаюча При k0 – зростаюча y =k/x - непарна функція |
У
0 Х
|
5 |
Cтепенева
функція
y = х
|
|
5.1 |
- довільне натуральне число D(y) = (-;) а) E(y)=[0;), при n=2k(n-парне) б) Е(y)=(-;), при n=2k+1(n-непарне) |
У У
0 Х 0 Х
а). б). |
5.2 |
- довільне ціле від’ємне число D(y) = (-;0)(0;) a)E(y) = (-;0)(0;), при =2n+1(- непарне) б)E(y) = (0;), при =2n (-парне)
|
0 Х 0 Х
а). б).
|
5.3 |
-довільне додатнє дробове число у=х , де = m/n a)D(y)=[0;) E(y)=[0;), при m=1; n=2k (n-парне) б)D(y)=(-;) E(y)=(-;), при m=1; n=2k+1 (n-непарне)
якщо m=m1, n=n1, де m1/n1 додатній нескорочуваний дріб в) D(y)=[0;) E(y)=[0;), при m1/n11 г) D(y)=[0;) E(y)=[0;), при 0m1/n11 |
У У
0 Х 0 Х
а) б)
У
0 Х 0 Х в) 1 г) 01 |
5.4 |
-довільне від’ємне дробове
y=x D(y)=]0;)E(y)=]0;)
|
0 Х |
5.5 |
-довільне ірраціональне число y = x a;б) D(y)=[0;), при 01 E(y)=[0;), при 1 в) D(y)=]0;) E(y)=]0;), при 0 |
У
0 Х 0 Х 0 Х а) б) в) |
6. |
Ціла частина числа х (“антьє х”); y=[x] Цілою частиною дійсного числа х називають найбільше ціле число, яке не перебільшує х. D(y)=(-;) E(y)=Z |
0 Х
|
7. |
Дробова частина числа х y={x}, {x} = x-[x] Дробовою частиною дійсного числа х, називають різницю між числом х та його цілою частиною D(y)=(-;) E(y)=[0;1[
|
У
1
0 Х |
8. |
Показова
функція
у = a D(y)=(-;) E(y)=]0;) а) при а1, y = a зростаюча б) при 0а1, y = a спадає
|
1 1 0 Х 0 Х а) при а1 б) при 0 а 1 |
9. |
Обернена функція y = f(x), та x = g(y) - взаємообернені функції D(y)=E(x) ; E(y)=D(x) Графіки взаємообернених функцій симетричні відносно прямої y = x |
У x=g(y)
y=f(x)
0 Х
|
10 |
Логорифмічна функція D(y)=]0;) E(y)=(-;) а) при а1 - зростаюча б) при 0 а 1 - спадаюча
|
0 Х 0 Х
а) при а1 б) при 0 а 1 |
Зауваження:
Число е. Функція
y=e![]() . Функція
y=lnx.
. Функція
y=lnx.
Серед показникових функцій y=a , де а1 особливе місце в математиці та її прикладних аспектах займає функція, що має слідуючі властивості: дотична до графіка цієї функції в точці (0;1) утворює з віссю ОХ кут 45. Основу такої показникової функції прийнято позначати буквою е, а саму функцію у=e називати експоненціальною функцією. Підраховано, що число е 2,7182818 ... , та встановлено , що е - ірраціональне число. Логарифмічну функцію, обернену до показникової у = е , тобто функцію y = logex прийнято позначати y = lnx і називати натуральним логарифмом. Графіки функцій y = lnx та у = е симетричні відносно прямої у = х.
 у
у
у = х
y=e
1
=45
0 1 х
y=lnx
Основні перетворення графіків функцій
Зауваження: Знаючи вигляд графіка функцій y = f(x), можна побудувати графіки функцій y = af(bx+c)+d, a також графіки функцій y=f(|x|); y=|f(x)|; y=|f(|x|)|; |y|=f(x) і.т.і.
Випадки, що часто зустрічаються при перетвореннях графіків функцій виділимо в окрему довідкову таблицю.
№ |
Графік функції |
Можна отримати з графіка функції y=f(x) за допомогою слідуючих перетворень |
1 |
y=f(x+c) |
При с>0 зсув ліворуч повздовж осі ОX на відрізок с |
2 |
y=f(bx); b>0
|
При b>1 стиск повздовж осі OX в b разів При 0<b<1 розтяг повздовж осі OX в b разів |
3 |
y=f(x)+d |
При d>0 зсув вгору повздовж осі ОY на відрізок d При d<0 зсув вниз повздовж осі ОY на відрізок d |
4 |
y=f(-x) |
Симетрия відносно осі ОY |
5 |
y=-f(x) |
Симетрія відносно осі ОX |
6 |
y=af(x); a>0 |
При a>1 розтяг повздовж OY в а разів При 0<a<1 стиск повздовж ОY в а разів |
7 |
y=af(bx+c) a>1; b>1; c>1 |
Послідовно : зсув ліворуч на с ; стиск по ОX в b разів , розтяг по ОY в а разів ,або af[b(x+c/b)]. Послідовно: стиск по OX в b разів, зсув ліворуч на с/b, розтяг по ОY в а разів. |
8 |
y=f(|x|) |
В правій напівплощині графік f(x) не змінюється, в лівій будується симетричний образ правої напівплощини відносно ОY. |
9 |
y=f(-|x|) |
В лівій напівплощині графік f(x) не змінюється, в правій будується симетричний образ лівої напівплощини відносно OY. |
10 |
y=|f(x)| |
Частина графіка f(x),що розташована в верхній напівплощині не змінюється частина графіка f(x) з нижньої напівплощини симетрично відбивається відносно осі OX. |
11. |
y=|f(|x|)| |
В правій напівплощині будується |f(x)|, а потім симетрично відбивається відносно осі OY. |
12 |
|y|=f(x) |
Залишають частину графіка f(x), що лежить над віссю OX і на осі OX та симетрично відбивають її відносно осі OX. |
13 |
|y|=f(|x|) |
В правій напівплощині залишають частину графіка f(x) що лежить над віссю OX та на осі OX, та симетрично відбивають відносно осі OY. Добавляють точки графіка y=f(x),що лежать на осі OX в лівій напівплощині. |
14 |
|y|=|f(|x|)| |
Будують спочатку y=|f(|x|), а потім симетрично відбивають його відносно OX. |
15 |
|y|=|f(x)| |
Будують спочатку графік y=|f(x)|, а потім симетрично відбивають його відносно OX. |

 Y
Y

 У
У 0
Х
0
Х
 У
У
У
У
 У
У
 У
У
 У У
У У У
У
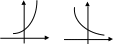 У
У
У
У
 У
У
У
У