МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

ОДЕСЬКА ДЕРЖАВНА АКАДЕМІЯ БУДІВНИЦТВА ТА АРХІТЕКТУРИ

КАФЕДРА ЗЕМЛЕУСТРОЮ ТА КАДАСТРУ

МЕТОДИЧНІ ВКАЗІВКИ

до виконання лабораторних та розрахунково-графічних робіт з дисципліни «Вища Геодезія»

(частина І )

для студентів 3-го курсу

Для студентів напряму 6.080101 – «Геодезія, картографія та землеустрій»

Освітньо кваліфікаційний рівень Бакалавр

Спеціальність «Землевпорядкування та кадастр»

Форма навчання денна та заочна

Одеса 2011 р.

«ЗАТВЕРДЖЕНО»

Вченою радою факультету ЕКУБ

Протокол № ____від_________

Методичні вказівки розглянуті і рекомендовані до друку на засіданні науково-методичної комісії факультету ЕкУБ, протокол №_____ від ________

Методичні вказівки розглянуті і рекомендовані до друку на засіданні кафедри «Землеустрій та кадастр», протокол №5 від 05.12.2011 р.

Укладачі: ст. викл. Колиханін С. П.

ас. Колосов О. В.

ас. Константінова О. В.

Рецензенти:

зав. кафедрою інженерної геодезії Одеської державної академії будівництва та архітектури, к.т.н., проф. Юрковський Р. Г.

зав. кафедрою гідрографії і морської геодезії Одеської національної морської академії, д.т.н., проф. Гладкіх І.І.

Відповідальний за випуск: зав. кафедрою «Землеустрою та кадастру»

к.т.н., доц. Хропот С.Г.

Лабораторна робота №1. Основні параметри земного еліпсоїда.

Е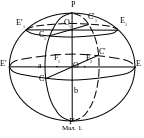 ліпсоїдом обертання називається геометричне тіло, утворене обертанням еліпса навколо його малої осі.

Земний еліпсоїд – еліпсоїд, який характеризує фігуру і розміри Землі.

Референц-еліпсоїд – земний еліпсоїд, прийнятий в конкретній країні для обробки геодезичних вимірів і встановлення системи геодезичних координат.

Позначення:

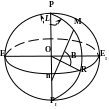
O – центр еліпсоїда; P – північний полюс; P’ – південний полюс; PP′ – вісь обертання еліпсоїда; F₁ и F₂ – точки фокусу еліпсоїда; a – велика піввісь; b – мала піввісь; ECE’C’ - екватор; E₁C₁E′₁C′₁ - паралель; PE₁EP′E′E′₁ и PC′₁C′P′CC₁ – меридіани.

Меридіаном називається переріз поверхні еліпсоїда площиною, що проходить через малу піввісь еліпсоїда. Меридіани являють собою еліпс. Наприклад, PE₁EP′E′E′₁ и PC′₁C′P′CC₁ – меридіани.

Паралеллю називається переріз поверхні еліпсоїда площиною, перпендикулярною до осі обертання еліпсоїда. Паралель являє собою коло. Наприклад, ECE′C′ и E₁C₁E′₁C′₁ – паралелі.

Найбільша паралель (ECE’C’), площина якої проходить через центр еліпсоїда О, називається екватором. Екватор є окружністю радіусу а, де а – велика піввісь еліпсоїда.

Лінійним ексцентриситетом називається відстань від центру еліпсоїда О до кожного з його фокусів F₁ або F₂. Лінійний ексцентриситет обчислюється за формулою:

(1.1)

де а – велика піввісь; b – мала піввісь.

Відношення лінійного ексцентриситету до великої півосі називається першим ексцентриситетом меридіанного еліпса:

(1.2)

де е – перший ексцентриситет.

Відношення лінійного ексцентриситету до малої півосі назівається другим ексцентриситетом меридіанного еліпсу:

(1.3)

де е^' – другий ексцентриситет.

Полярне стиснення еліпсоїда обчислюється за формулою:

(1.4)

де a и b - велика і мала півосі еліпсоїда.

Лінійні величини a та b (велика і мала півосі) визначають розміри еліпсоїда.

Відносні величини α, е и е^' (полярне стиснення, перший і другий ексцентриситети) визначають форму еліпсоїда, тобто більшу чи меншу приплюснутості біля полюсів.

У геодезії застосовують також і інші відносні величини, які не мають загальноприйнятої назви:

(1.5)

(1.6)

Основна властивість еліпса: сума відстаней від будь-якої точки еліпса до його фокусів є постійною величиною, рівною 2а.

Р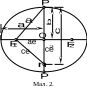 озміри еліпса визначаються розмірами його великої півосі а. Форма еліпса визначається однією з наведених вище відносних величин, найчастіше стисненням α.

Крім великої і малої півосей еліпса, часто застосовується ще одна лінійна величина, що визначається рівністю

(1.7)

Ця величина дорівнює гіпотенузі прямокутного трикутника РF₁n (мал. 2).

Завдання 1.1. В трикутнику РF₁n мал 2.) кут РF₁n прямий. Довести, що:

Завдання 1.2. Користуючись формулами (1.2) – (1.7) довести, що:

(1.8)

Завдання 1.3. Користуючись формулами (1.2) – (1.8) довести основні залежності між елементами еліпса:

(1.9)

(1.10)

(1.11)

(1.12)

(1.13)

(1.14)

(1.15)

Так як елементи еліпса є одночасно елементами еліпсоїда обертання, утворенням якого є цей еліпс, то і відносини між елементами еліпса справедливі для відносин між елементами еліпсоїда.

У нашій країні в даний час застосовуються референц-еліпсоїд Красовського (а = 6378245 м, α = 1:298,3) і загальноземний еліпсоїд (а = 6378137 м, α = 1:298,2572221).

Завдання 1.4. З відомих елементів еліпсоїда Красовського а = 6378245 м. і =1:298,3 (з точністю для лінійних елементів - 4 знаки після коми, для відносних елементів - 10 знаків після коми) обчислити: