15.7. Последовательность решения задач по определению скоростей соударяющихся тел
Задачи об определении скоростей соударяющихся тел в конце центрального косого частично упругого удара решать в последовательности:
1) направить ось n вдоль линии центра, ось τ - перпендикулярно к ней;
2)
вычислить проекции на оси n
и τ скоростей
соударяющихся тел в начале удара;
3)
вычислить проекцию общей скорости
соударяющихся тел на ось n
в конце неупругого удара по формуле
;
4)
вычислить проекции скоростей
,
,
,
соударяющихся тел на оси n
и τ
в конце удара по формулам:
,
,
,
;
5) определить скорости обоих тел в конце удара.
Модули скоростей равны:
,
.
Направление скоростей определяется формулами:
,
.
При ударе тела о неподвижную плоскость следует считать массу неподвижной плоскости бесконечно большой, а скорость до удара равной нулю (m2= ∞, v2=0). В случае центральных прямых ударов двух тел вычисления упрощаются, так как проекции скоростей на ось τ обращается в нуль.
Задача 3.28. Шар веса Р1=10 Н ударяется о неподвижный шар веса Р2=20 Н (рис. 3.101). Какую скорость v1 должен иметь центр тяжести первого шара до удара, для того чтобы после неупругого удара их общая скорость равнялась 6 м/c?
Рис. 3.101
Решение. Ось n направим вдоль линии центров С1С2 налево, как показано на рисунке. Проекции скоростей центров тяжести шаров на ось n в начале удара имеют вид:
.
Проекция общей скорости шаров на ось n в конце неупругого удара равна
.
Из
этого соотношения находим проекцию
искомой скорости
центра тяжести первого шара в начале
неупругого удара:
Тригонометрические величины
|
|
|
|
|
|
|
0o |
0 |
1 |
0 |
|
1 |
|
30o |
|
|
|
|
|
2 |
45o |
|
|
1 |
1 |
|
|
60o |
|
|
|
|
2 |
|
90o |
1 |
0 |
|
0 |
|
1 |
Градусная и радианная мера
Углы в градусах |
360о |
180о |
90о |
60о |
45о |
30о |
Углы в радианах |
2 |
|
|
|
|
|
Формулы приведения
Функции |
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Табличные дифференциалы
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
Табличные интегралы
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
.
\
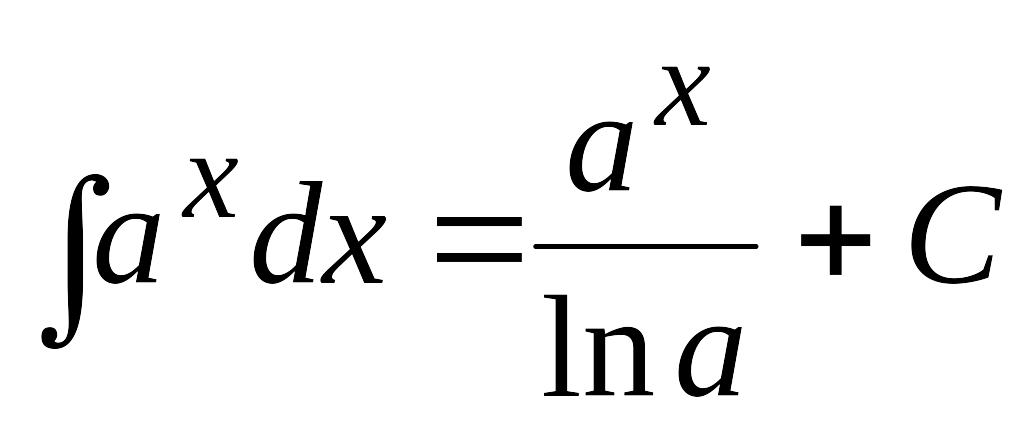