15.3. Классификация видов удара

Линией центров назы­вается ось, проходящая че­рез центры тяжести соуда­ряющихся тел.

Удар называется цен­тральным, если точка К со­прикосновения соударяю­щихся тел лежит на линии центров , а касательная плоскость, проведенная в точке соприкосновения к поверхностям этих тел, перпендикулярна к линии центров (рис. 3.94, а).

а) б)

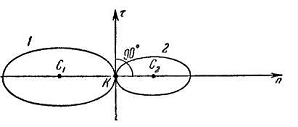
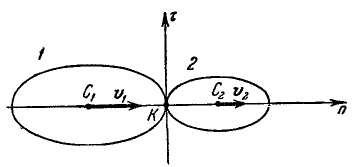
Рис. 3.94

Удар называется прямым, если скорости центров тяжести соуда­ряющихся тел в начале удара лежат на линии центров (рис. 3.96, б).

Если хотя бы одна из ско­ростей центров тяжести соуда­ряющихся тел в начале удара не лежит на линии центров, то удар называется косым (рис. 3.95).

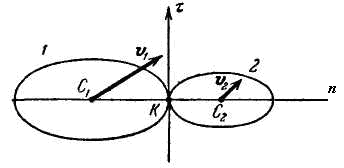
Рис. 3.95

В зависимости от степени вос­становления недеформированного состояния удары разделяются на неупругие, частично упру­гие и упругие.

Удар называется упругим, если недеформированное состояние пол­ностью восстанавливается (k=1,0).

Удар называется частично упругим, если недеформированное со­стояние не полностью восстанавливается. В конце удара центры тяжес­ти тел движутся с разными скоростями (0<k<1,0).

Удар называется не­упругим, если недеформированное состояние со­ударяющихся тел не вос­станавливается. В конце удара центры тяжести тел движутся с одинаковыми скоростями (k=0).

Для рассмотрения прямого центрального неупругого удара двух тел введем обозначения (табл. 3.2).

Таблица 3.2

Номер тела	Масса тела	Скорости
		В начале удара	В конце удара
1			u
2			u

Тогда проекция на ось п (рис. 3.96) общей скорости соударяю­щихся тел в конце удара равна

(ось п проведена вдоль линии центров).

Импульс мгновенной силы определяется формулой

.

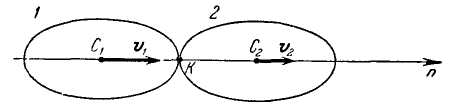
Рис. 3.96

Для рассмотрения прямого центрального частично упругого удара двух тел разделим процесс удара на два этапа. В течение первого этапа совершается деформация соударяющихся тел. В течение второго этапа — частичное восстановление недеформированного состояния. В момент окончания первого этапа и начала второго центры тяжести тел обладают одинаковыми скоростями, которые они имели бы в конце соответствующего неупругого удара. В конце второго этапа центры тяжести тел имеют уже различные скорости и . Введем обозначения (табл. 3.3):

Таблица 3.3

Номер тела	Масса тела	Скорости
		В начале удара	В конце I этапа	В конце II этапа
1 2		I этап	u u	II этап

Тогда проекции на ось п соударяющихся тел в конце удара равны

; ,

где

(ось п проведена вдоль линии центров). Из этих формул можно получить выражение коэффициента восстановления

,

которое иногда используется в качестве определения этого понятия.

В случае упругого удара, т. е. при k=1:

; .

Для рассмотрения прямого частично упругого удара тела о непо­движную плоскость введем обозначения (табл. 3.4):

Таблица 3.4

Номер тела	Масса тела	Скорости
		В начале удара	В конце I этапа	В конце удара
1 2		0	0 0	0

Тогда проекция на ось п скорости центра тяжести падающего тела в конце удара равна , причем , где - высота свободного падения тел на неподвижную плоскость, - высота отражения тела после частично упругого удара (рис. 3.97).

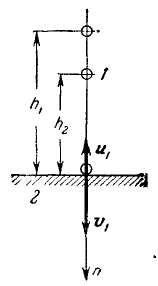
Рис. 3.97

При рассмотрении косого центрального ча­стично упругого удара двух тел поверхно­сти соударяющихся тел считаются абсолютно гладкими. Ось п проводится вдоль линии центров (рис. 3.98). Ось перпендикулярна к оси п. Проекции скоростей центров тяжести со­ударяющихся тел в начале удара имеют вид

.

Проекции скоростей центров тяжести соударяющихся тел в конце удара (рис. 3.99) равны:

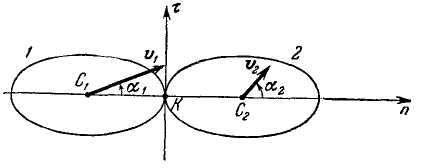
Рис. 3.98

где

;

; .

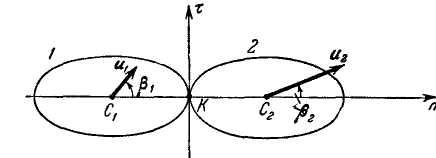
Рис. 3.99

Модули скоростей центров тяжести соударяющихся тел в конце удара равны:

.

При изучении косого частично упругого удара тела о неподвижную плоскость поверхности тела и неподвижной плоскости считаются абсолютно гладкими. Направления осей п и указаны на рис. 3.100.

Проекции скорости центра тяжести падающего тела в начале уда­ра имеют вид:

.

Проекции скорости центра тяжести падающего тела в конце удара равны:

Модуль скорости центра тяжести падающего тела в конце удара определяется формулой

.

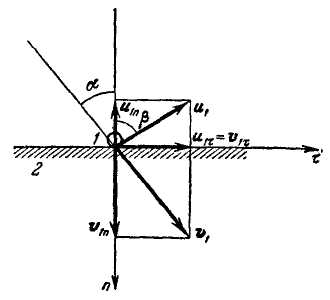
Рис. 3.100

Коэффициент восстановления вычисляется по формуле , где — угол падения, — угол отражения.