14.3. Вариационный принцип Гамильтона — Остроградского

После соответствующих математических преобразований общее уравнение динамики примет вид

. (3.33)

Ограничим произвольность выбора путей сравнения условием пересечения действительной траектории и кривой сравнения в мо­менты времени и , т. е. условием, чтобы при и (рис. 3.93):

. (3.34)

Рис. 3.93

Кривые сравнения должны выбираться из класса дважды диф­ференцируемых функций.

Так как по условию (3.50) вариации радиуса-вектора на границах равны нулю, то имеем

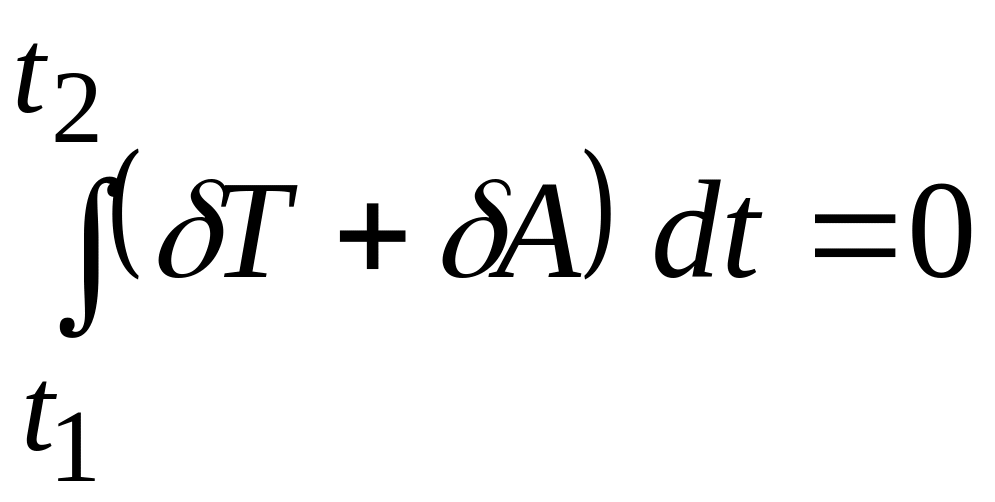. (3.35)

Это уравнение выражает принцип Гамильтона —Остроградского: действительное движение механической системы с голономными дву­сторонними идеальными связями отличается от всех иных возможных ее движений, удовлетворяющих условию (3.34) тем, что только для действительного движения выпол­няется равенство (3.35).

В том случае, если раздельно рассматривать работу задаваемых консервативных и неконсервативных сил, уравнение (3.35) можно представить в следующем виде:

,

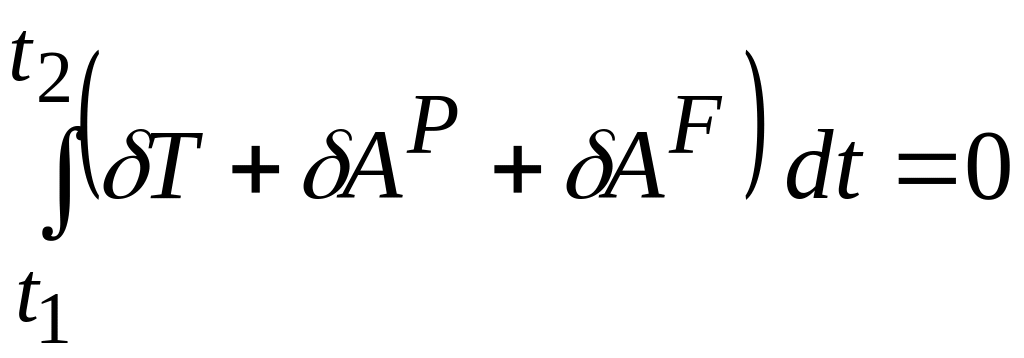где — элементарная работа консервативных сил, а — элементарная работа неконсервативных сил.

Для консервативной системы выражение принципа Гамильтона — Остроградского имеет вид

.

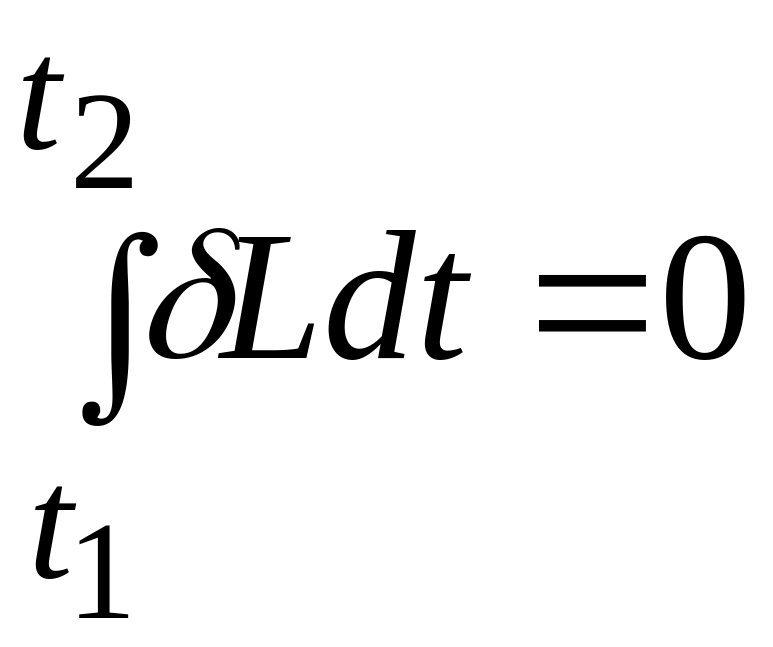Введем обозначение

,

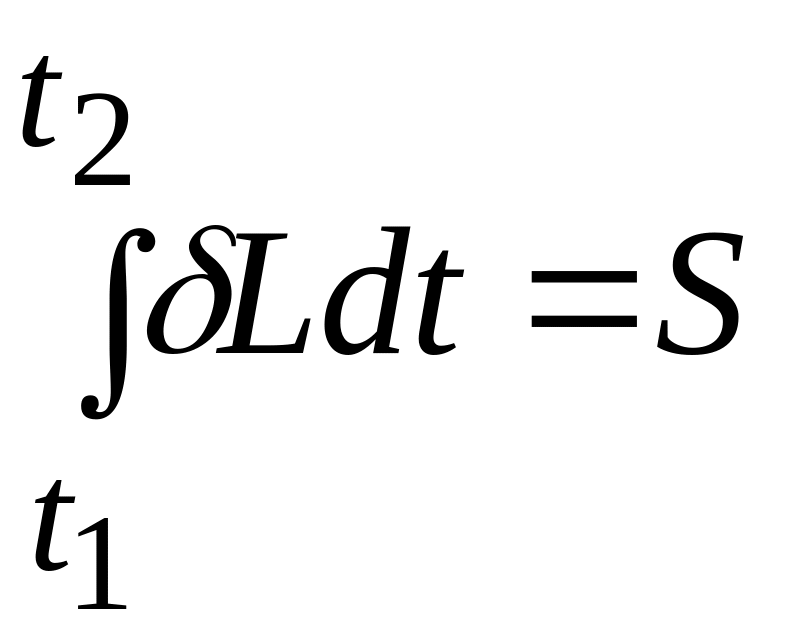где величина S называется действием по Гамильтону.

Размерность величины S есть работа, умноженная на время (единицы измерения в системе МКС — кг∙м²/с, в технической сис­теме — кгс∙м∙с).

Глава 15. Теория удара

15.1. Явление удара

Ударом называется взаимодействие тел, в результате которого за бесконечно малый промежуток времени скорости точек изменяются на конечную величину.

Ударной силой называется сила, возникающая при мгновенном

взаимодействии тел и достигающая больших значений за бесконечно малый промежуток времени.

Временем удара называется промежуток времени τ действия ударной силы.

Ударным импульсом называется векторная величина

.

В теории удара принимают следующие допущения; скорости точек практически мгновенно изменяются на конечную величину; импульсами неударных сил и перемещениями точек за время удара как бесконечно малыми величинами пренебрегают.

В результате удара скорость точки до удара становится равной после удара.

Изменение количества движения материальной точки за время удара τ определяется следующей теоремой: изменение количества движения материальной точки за время удара равно ударному импульсу, приложенному к точке

. (3.36)

Уравнение (3.36) называется основным уравнением теории удара.

Коэффициентом восстановления при ударе о неподвижную поверхность называется отношение числового значения скорости после удара к числовому значению скорости до удара, т.е.

.

15.2. Теорема об изменении количества движения

механической системы при ударе

Теорема об изменении количества движе­ния механической системы при ударе формулируется так: изменение количества движения механической системы за время удара равно геометрической сумме всех внешних ударных импульсов, приложенных к точкам системы.

, (3.37)

где - количество движения механической системы в момент окончания действия ударных сил; - количество движения механической системы в момент начала действия ударных сил.

Векторному уравнению (3.37) соответствуют три уравнения в проек­циях на оси координат:

(3.38)

Эти уравнения показывают, что изменение проекции количества дви­жения системы на любую ось равно сумме проекций на ту же ось всех внешних ударных импульсов, приложенных к системе.

Количество движения механической системы можно выразить через массу всей системы m и скорости центра масс системы по формулам и . Подставим эти значения в уравнение (3.37)

. (3.39)

Уравнение (3.39) определяет изменение скорости центра масс системы при ударе. Векторному уравнению (3.39) соответствуют три уравнения в проекциях на оси координат:

(3.40)

Эти уравнения определяют изменение проекции скорости центра масс на любую ось при ударе. Из уравнений (3.37) и (3.38) при отсутствии внешних ударных импуль­сов имеем

.

т.е. при действии на механическую систему лишь внутренних ударных импульсов количество движения системы не изменяется.

Таким образом, удары, возникающие при столкновении тел, входящих в одну механическую систему, не могут вызвать изменения количества движения системы, т. е. скорости движения ее центра масс.