13.5. Малые свободные колебания механической системы с одной степенью свободы
Состояние покоя (равновесия) механической системы может быть устойчивым, неустойчивым и безразличным (рис. 3.89). Состояние покоя механической системы называется устойчивым, если система, выведенная из положения покоя, совершает колебания около этого положения.
Неустойчивое - если при сколь угодно малом отклонении системы из положения покоя она удаляется от этого положения и колебаний не возникает.
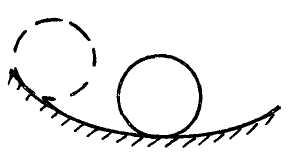
Устойчивое Неустойчивое Безразличное
Рис. 3.89
Безразличное - если при отклонении ее из положения покоя система и в новом положении может остаться в состоянии покоя.
Условие равновесия механической системы вытекает из принципа возможных перемещений: необходимым и достаточным условием равновесия механической системы с идеальными связями является равенство нулю суммы элементарных работ всех активных сил на любом возможном ее перемещении, т.е.
.
В обобщенных координатах
.
Умножим
обе части равенства на
.
Правая часть будет равна нулю только в том случае, если сомножитель обобщенной координаты ноль, то есть для равновесия механической системы необходимо и достаточно, чтобы все обобщенные силы, соответствующие обобщенным координатам, были равны нулю.
-
условие равновесия.
Для консервативной системы
.
По уравнению равновесия консервативной системы нельзя судить об устойчивости состояния покоя.
Условие устойчивости состояния покоя содержится в теореме Лагранжа - Дирихле: те положения покоя консервативной системы, в которых потенциальная энергия системы достигает минимума, являются ее устойчивыми состояниями.
- условие наличия состояния покоя,
-
условие устойчивого состояния покоя.
Для описания колебательного движения механической системы в обобщенных координатах используется уравнение Лагранжа II рода:
,
(а)
где (а) - дифференциальное уравнение движения механической системы;
Т
- кинетическая энергия, приводимая к
виду
(а
- обобщенный коэффициент инерции); П
- потенциальная энергия, приводимая к
виду
(с – обобщенный коэффициент жесткости);
- обобщенная скорость; q
- обобщенная координата; Q
- обобщенная сила.
Если на механическую систему действуют только консервативные силы, то
.
После приведения кинетической энергии к виду , потенциальной энергии к виду и преобразований, указанных в уравнении Лагранжа II рода, получим
.
Поделив
обе части равенства на а
и произведя замену —
,
запишем дифференциальное уравнение
свободных колебаний системы с одной
степенью свободы без учета сил
сопротивления
,
где
k
- циклическая (круговая) частота колебаний,
размерность рад/с
или
.
Период свободных колебаний системы определяется по формуле
.
Решение дифференциального уравнения свободных колебаний записывается в виде
.
Амплитуда колебаний А и начальная фаза колебаний α определяются по начальным условиям движения.
Задача
3.27. Определить
циклическую частоту свободных колебаний
механической системы с одной степенью
свободы (рис. 3.90), состоящей из груза 1
массой
кг,
колеса 2 массой
кг,
радиус которого R
= 2 м,
радиуса инерции
м,
коэффициент жесткости пружины с
= 40 Н/см.
Трением, массами нити и пружины
пренебречь.
Решение.
Приведем систему в движение и покажем
направления скоростей тел
,
,
.
Пусть тело 1 опускается со скоростью
,
тогда колесо 2, совершая плоское движение,
будет иметь угловую скорость
,
направленную против хода часовой
стрелки. В точке контакта колеса и
поверхности находится мгновенный центр
скоростей.
Обозначим буквой А точку прикрепления пружины к колесу. Скорости точек С и А должны быть пропорциональны их расстояниям до мгновенного центра скоростей.
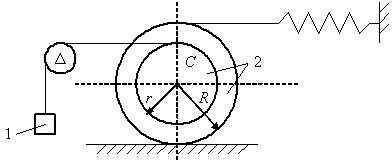
Рис. 3.90
Активными
силами в задаче будут
и
.
Принцип освобождаемости от связей
применим только к внешним связям
(поверхность качения и упругая связь -
пружина), иначе нельзя описать поведение
всех тел системы одним уравнением (рис.
3.91).
Отбрасывая
неподвижную поверхность, показываем
нормальную реакцию
и силу трения, так как по абсолютно
гладкой поверхности качение тела 2
невозможно. Силу трения
изобразим в сторону, противоположную
скорости центра масс
.
Мысленно отбросив пружину, покажем силу
упругости
,
направив ее противоположно
.
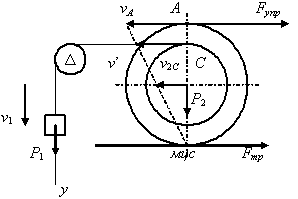
Рис. 3.91
Задачу решаем в обобщенных координатах. За q можно принять и угол поворота 2-го тела и вертикальную координату 1-го тела, выбор не изменит конечного результата, изменяется только уравнение связей.
Пусть q =y, покажем ось у на рисунке.
Уравнение Лагранжа I I рода
.
Обобщенная сила
.
Сила трения в нашей задаче работу совершить не может, так как приложена все время движения к точке, скорость которой равна нулю. Это означает, что обобщенная сила определяется только для консервативных (потенциальных) сил, т.е.
.
Дифференциальное уравнение малых колебаний этой системы имеет вид
,
,
где с - обобщенный коэффициент жесткости; а - обобщенный коэффициент инерции.
Значения обобщенных коэффициентов получим, записав кинетическую и потенциальную энергию системы.
Кинетическая энергия системы равна сумме кинетических энергий каждого тела системы и должна быть приведена к виду
.
Тело 1 совершает поступательное движение, поэтому кинетическую энергию запишем в виде
.
Тело 2 совершает плоское движение, кинетическая энергия в этом случае
.
Для системы
.
Составим уравнения связей, выразив все скорости через обобщенную скорость^
;
(а)
.
Скорость точки схода гибкой связи с малого барабана такая же как у тела 1, так как связь идеальна. Тогда
или
.
(б)
Подставим
(б) в формулу для
.
(в)
Теперь подставим (а), (б) и (в) в выражение кинетической энергии
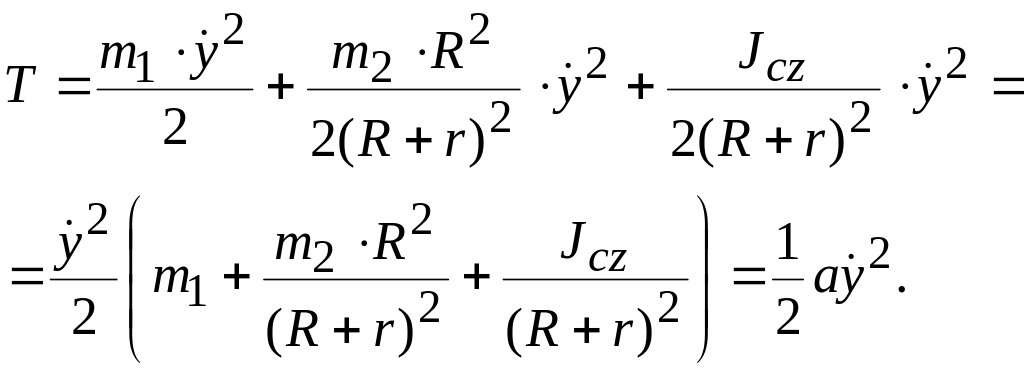
Коэффициент
инерции системы (выражение, заключенное
в квадратные скобки) содержит только
постоянные и известные значения (
),
т.е. это просто число, если задача решается
в числовых параметрах.
Потенциальная энергия П системы численно равна работе потенциальных сил, которую необходимо совершить, чтобы вернуть систему из отклоненного положения в положение равновесия. П приводится к виду
.
Для
системы
.
.
Здесь
,
так как точка приложения силы не
перемещается по вертикали.
;
,
где
-
система не может быть так организована,
чтобы статическое удлинение пружины
отсутствовало.
Для определения конечного удлинения пружины х удобнее записать скорость точки А, выразив ее через обобщенную скорость, а затем эту зависимость проинтегрировать
.
Проинтегрировав при нулевых начальных условиях, получим перемещение точки А:
.
Окончательно конечное удлинение пружины
;
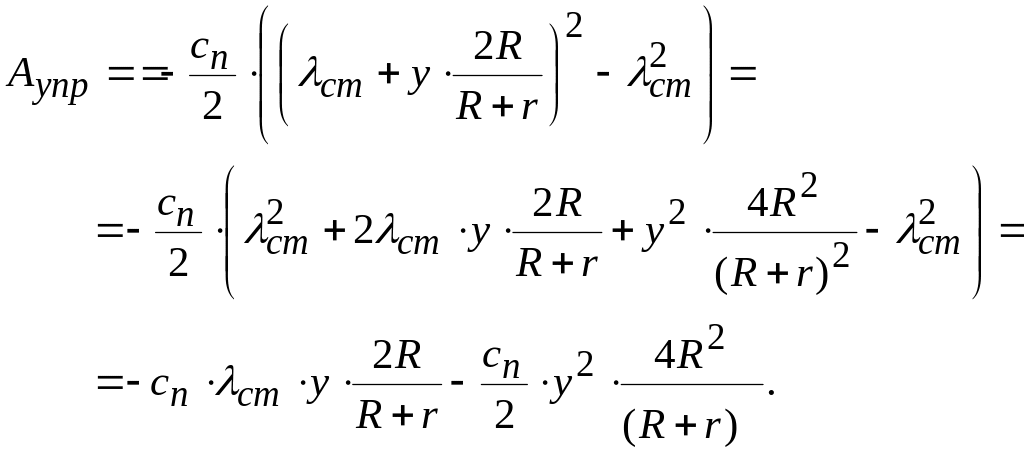
Потенциальная энергия системы
.
Это выражение содержит слагаемые с обобщенной координатой у в первой степени, что не соответствует общему виду П (см. начало пункта 4).
Используя критерий Лагранжа-Дирихле, запишем:
,
т.е. в положении равновесия (у =0) два первых слагаемых в сумме дают 0, поэтому можем сделать вывод, что для осуществления колебаний системы имеет значение только третье слагаемое.
Таким образом, потенциальную энергию системы запишем как
.
В квадратных скобках записан обобщенный коэффициент жесткости системы, это тоже постоянное значение, то есть число.
Циклическая частота колебаний.
.
При
решении задачи было проверено наличие
положения равновесия. Это можно сделать,
не используя критерий Лагранжа-Дирихле,
а вспомнив статику: в положении равновесия
силы
и
создают моменты относительно мгновенного
центра скоростей с противоположными
знаками, но равными модулями
,
т.е.
.
В положении равновесия эти две силы уравновешивают друг друга.
Можно также заметить, что если пружина жестко прикреплена к колесу, а не намотана свободным концом на него, то результат задачи будет приблизительным.