5.3. Угловое ускорение тела при сферическом движении

При сферическом движении тела положение мгновенной оси вра­щения со временем изменяется, а следовательно, изменяется не только модуль, но и направление вектора угловой скорости тела. Векторная величина, характеризующая изменение угловой скорости в данный момент времени называется мгновенным угловым ускорением. Вектор углового ускорения равен производной от вектора угловой скорости по времени

.

Рис. 2.89

Направление вектора углового ускорения не совпадает с мгновенной осью вращения (рис. 2.89).

5.4. Скорости точек твердого тела при сферическом движении

Скорости точек твердого тела, совершающего сферическое движе­ние, в каждый момент времени определяются как их вращательные скорости при вращении вокруг мгновенной оси ОΏ (рис. 2.90). Из этого вытекает, что любая точка тела имеет в данный момент времени такую же скорость, какую она имела бы при вращении тела с угловой скоростью вокруг неподвижной оси, совпадающей с мгновенной осью.

Модуль скорости точки

,

где h_Ώ — расстояние от точки до мгновенной оси вращения.

Рис. 2.90

Распределение скоростей то­чек тела в данный момент времени t при сфери­ческом движении по отношению к мгновенной оси вращения не отличается от распределения ско­ростей при вращении тела вокруг неподвижной оси.

Проекции скорости точки на неподвижные оси декартовых координат определяются по форму­лам Эйлера:

Проекции скорости на подвижные оси декартовых координат определяются по аналогичным формулам (рис. 2.91):

Рис. 2.91

Если положение мгновенной оси Ώ уже установлено, то для нахож­дения угловой скорости достаточно знать скорость какой-либо точки А, не лежащей на мгновенной оси (рис. 2.92). Тогда, опустив из этой точки перпендикуляр АК на мгновен­ную ось Ώ , получим

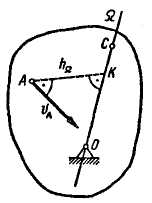
Рис. 2.92

откуда

т. е. для определения модуля угловой скорости тела следует модуль скорости точки разделить на расстояние от точки А до мгно­венной оси вращения.

5.5. Ускорения точек твердого тела при сферическом движении

Теорема Ривальса: ускорение любой точки твердого тела при сферическом движении определяется как геометрическая сумма ее вращательного и осестремительного ускорений (рис. 2.93).

Здесь — вращательное ускорение точки; — осестремительное (центростремительное) ускорение точки.

Вектор вращательного ускорения точки направлен перпен­дикулярно плоскости, проходящей через вектор углового ускорения и радиус-вектор точки , в ту сто­рону, откуда поворот вектора к вектору на наименьший угол ви­ден происходящим в сторону, об­ратную вращению часовой стрелки.

Рис. 2.93

Модуль вращательного ускоре­ния

,

где =МК₁ - расстояние от точки М до оси углового ускорения Е.

Вектор осестремительного ускорения направлен перпендикулярно векторам угловой ско­рости и линейной скорости точки , т. е. по перпендикуляру, опу­щенному из точки М на мгновенную ось Ώ, в ту сторону, откуда поворот вектора , условно отложенного в точке М, к вектору на наименьший угол виден происходящим в сторону, обратную враще­нию часовой стрелки.

Модуль осестремительного ускорения

,

где h_Ώ = MК₂ — расстояние от точки М до мгновенной оси Ώ.

Модуль ускорения точки как диагонали параллелограмма ускорений

или

Вращательное ускорение точки при сферическом движении тела определяется относительно оси углового ускорения Е и направлено перпендикулярно плоскости, проходящей через вектор углового уско­рения и радиус-вектор (перпендикулярно h_Е), т. е. и . Следовательно, направление не совпадает с направлением скорости точки .

Вращательное и осестремительное ускорения точки и при сферическом движении не следует смешивать с ее касательным и нормальным ускорениями и .