4.4. Мгновенный центр скоростей

При плоском движении плоской фигуры в каждый момент времени существует точка, связанная с плоской фигурой, скорость которой в этот момент равна нулю. Эту точку называют мгновенным центром скоростей. Пусть известны скорость некоторой точки О плоской фигуры (рис. 2.55) и угловая скорость фигуры в некоторый момент времени. Примем точку О за полюс. Тогда скорость любой точки фигуры будет равна геометрической сумме скорости полюса и вращательной скорости точки вокруг этого полюса. Восставим в точке О перпен­дикуляр к скорости так, чтобы направление поворота скорости к этому перпендикуляру совпадало с направлением вращения фигуры.

Вращательные скорости всех точек этого перпендикуляра вокруг полюса О направлены противоположно скорости полюса.

Найдем такую точку Р, вращательная скорость которой равна по модулю скорости полюса , т.е. = . Так как направления этих скоростей противоположны, то = - . Скорость точки Р

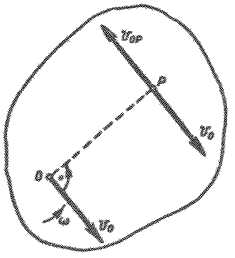
Рис. 2.55

Следовательно, точка Р в рассматриваемый момент времени является мгновенным центром скоростей.

Определим положение точки Р. Вычислим вращательную скорость точки Р вокруг полюса О и приравняем ее скорости полюса

откуда

Следовательно, мгновенный центр скоростей плоской фигуры на­ходится на перпендикуляре к направлению скорости полюса на рас­стоянии от полюса, равном .

4.5. Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей

Скорость любой точки плоской фигуры в данный момент времени представляет собой вращательную скорость этой точки вокруг мгновенного центра скоростей, поэтому

т. е. скорость любой точки плоской фигуры в каждый момент времени имеет модуль, равный произведению угловой скорости фигуры на длину отрезка, соединяющего точку с мгновенным центром скоростей, и направлена перпендикулярно этому отрезку в сторону вращения фигуры.

Модули скоростей точек плоской фигуры в каждый момент вре­мени пропорциональны расстояниям от этих точек до мгновенного центра скоростей.

Следовательно, чтобы определить скорости точек плоской фигуры с помощью мгновенного центра скоростей, необходимо знать положение мгновен­ного центра скоростей и угловую скорость фигуры.

4.6. Различные случаи определения положения мгновенного центра скоростей

1. Известны прямые, по которым направлены скорости двух точек плоской фигуры А и В (рис. 2.56). В этом случае мгновенный центр скоростей фигуры определится как точка пересечения перпендикуляров к этим прямым, восставленных в точках А и В.

2. Если скорости двух точек А и В плоской фигуры параллельны и не перпендикулярны АВ (рис. 2.57), то мгновенный центр скоростей находится в бесконечности (АР = ∞).

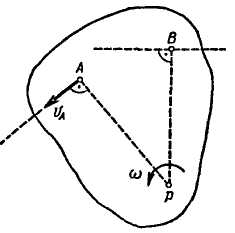
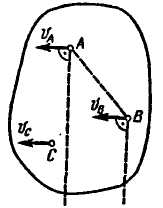
Рис. 2.56 Рис. 2.57

3. Если плоская фигура катится без скольжения по некоторой неподвижной поверхности (рис. 2.58), мгновенный центр скоростей находится в точке соприкасания фигуры с поверхностью.

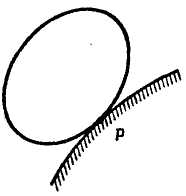
Рис. 2.58

4. Если скорости точек А и В плоской фигуры параллельны между собой и перпендикулярны АВ, то для определения положения мгно­венного центра скоростей должны быть известны модули скоростей обеих точек А и В (рис. 2.59, а, б). Известно, что модули скоростей точек фигуры пропорциональны их расстояниям от мгновенного центра скоростей, т. е.

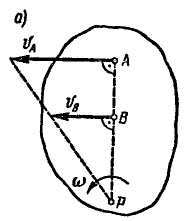
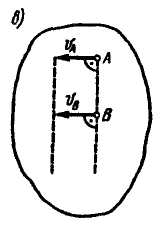
Рис. 2.59

Следовательно, концы скоростей точек А и В лежат на прямой, проходящей через мгновенный центр скоростей. Пересечение этой пря­мой с прямой АВ определяет мгновенный центр скоростей фигуры.

Если скорости точек А и В плоской фигуры равны, параллельны между собой и перпендикулярны АВ (рис. 2.59, в), то мгновенный центр скоростей находится в бесконечности (АР = ∞), а угловая скорость фигуры

Задача 2.11. Колесо радиуса R = 0,5 м катится без скольжения по прямолинейному участку пути; скорость центра его постоянна и равна =10 м/с. Найти скорости концов и (рис. 2.60) вертикального и горизонтального диаметров колеса. Определить его угловую скорость.

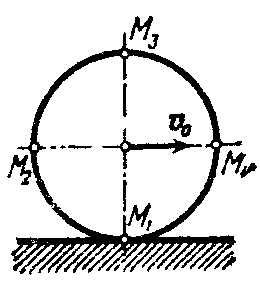
Рис. 2.60

Решение. Мгновенный центр скоростей лежит в М₁

м/с;

м/с; м/с; .

Задача 2.12. Каток в виде цилиндра радиуса R = 2 м катится по горизонтальной плоскости с угловой скоростью ω = 20 рад/c. Определить скорость точки С касания катка с плоскостью, если известно, что скорость точки В направлена вертикально вниз, а угол  α = 45^о (рис. 2.61, а).

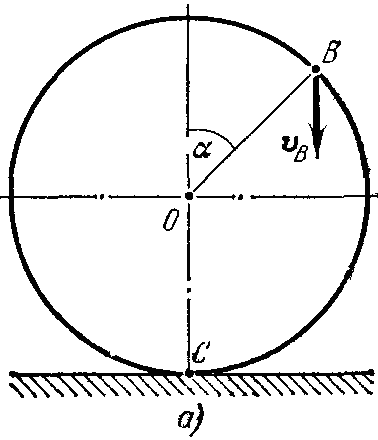
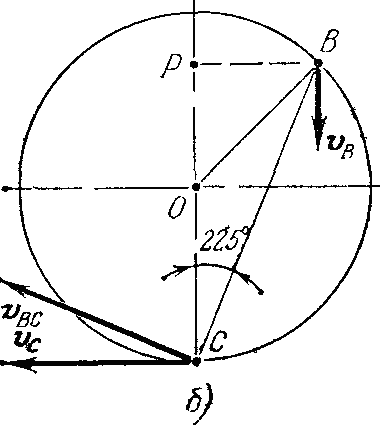
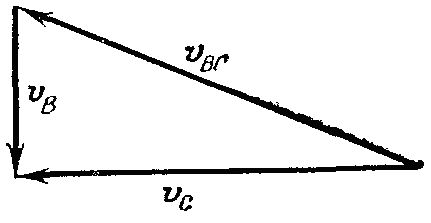
Рис. 2.61

Решение. Графический способ. Скорость точки С состоит из двух слагаемых (рис. 2.58, б)

. (2.14)

Известны направления всех трех векторов, входящих в (2.14), и величина скорости

.

Из треугольников ОВС находим ВС=2R·cos 22,5^о. Следовательно,

м/c.

Этих условий достаточно для построения треугольника скоростей. Построив треугольник скоростей (рис. 2.62, в) в выбранном масштабе, получаем

м/c.

Решим данную задачу аналитическим способом. Спроецируем равенство (2.14) на горизонтальную ось. Получим

м/c.

Можно решить данную задачу третьим способом. Найдем мгновенный центр скоростей Р. Тогда

.

Из треугольника ВСР находим . Тогда

м/с.

Задача 2.13. Ползуны А и В (рис. 2.63,a), соединенные шарнирно с линейкой АМ эллипсографа, перемещаются по двум взаимно перпендикулярным направляющим. Расстояние АВ и ВМ равны соответственно l и а. Определить скорости точек В и М линейки и ее угловую скорость, если в рассматриваемый момент , а .

а) б)

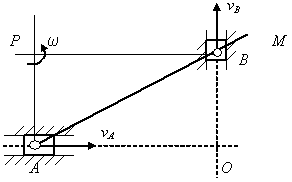
Рис. 2.63

Решение. Скорости точек А и В линейки направлены вдоль направляющих, по которым движутся ползуны. Восстанавливая в этих точках перпендикуляры к скорости и линии действия , находим мгновенный центр скоростей линейки Р (рис. 2.63,б). Скорости точек линейки пропорциональны их расстояниям от мгновенного центра Р, т.е.

,

отсюда

.

Расстояния АР и ВР (мгновенные радиусы) находим из прямоугольного треугольника АРВ, а расстояние МР – из треугольника РВМ:

, ,

.

Таким образом,

.

Угловая скорость линейки .