
- •1 Метод Гаусса (lu-разложений).
- •2 Нахождения определителя матрицы методом Гаусса.
- •3 Уточнение решения полученного методом Гаусса.
- •4 Нахождение элементов обратной матрицы методом Гаусса.
- •Пусть дана слау
- •29 Квадратурные формулы Ньютона-Котеса.
- •Свойства коэффициентов Ньютона-Котеса.
- •30 Формула трапеций.
- •Оценим остаточный член:
- •31 Формула Симпсона ( параболы).
- •32 Квадратурные формулы Ньютона-Котеса.
- •Свойства коэффициентов Ньютона-Котеса.
- •33 Квадратурные формулы наивысшей степени точности.
- •Свойства.
- •34 Интегрирование быстроосциллирующих функций.
- •Существование и единственность задачи Коши дается в теореме Пикара.
- •36 Метод Пикара.
- •37 Метод Эйлера.
- •Т.Е. Хоть и не сказано о том, что выполняется условие Липшица, но зато ограничено, и мы можем оценить | |l.
- •48 Метод правой прогонки.
- •49. Метод левой прогонки.
- •51 Метод Либмана.
- •Рассмотрим уравнение эллиптического типа – уравнение Пуассона:
- •53 Метод сеток для решения уравнений параболического типа.
- •8. Итерационные методы решение систем линейно-алгебраических уравнений.
- •Пусть дана слау
- •9. Метод простых итераций для решения линейно-алгебраических уравнений.
- •Нормы векторов и матрицы.
- •11. Метод Зейделя. Условия сходимости метода
- •1.Теорема об lu-разложении кв. Матрицы. Метод Гаусса решения слау.
- •Теорема: (об lu – разложений матрицы).
- •Методика решения.
- •2. Теорема об lu-разложении кв. Матрицы. Нахождения определителя матрицы методом Гаусса. Теорема: (об lu – разложений матрицы).
- •Нахождения определителя матрицы методом Гаусса
- •3.Уточнение решения полученного методом Гаусса.
- •4. Нахождение элементов обратной матрицы методом Гаусса.
- •Пусть дана слау
- •14. Проблема собственных значений. Метод Данилевского.
- •Метод а.М. Данилевского
- •Теорема: Преобразование подобия не изменяет собственных значений матрицы.
- •15. Проблема собственных значений. Степенной метод .
- •Степенной метод.
- •Обозначим соответствующие собственные векторы через
- •Степенной метод имеет задачу нахождения пары:
- •17. Скалярное нелинейное уравнение.Метод половинного деления (дихотомии).
- •Требуются решить уравнение: (1), другими словами – найти нули функции, т.Е. Такие , которые обращают уравнение (1) в тождество.
- •Метод половинного деления
- •12.Метод вращения решения слау
- •18.Скалярное нелинейное уравнение. Метод хорд.
- •Требуются решить уравнение: (1), другими словами – найти нули функции, т.Е. Такие , которые обращают уравнение (1) в тождество.
- •18. Скалярное нелинейное уравнение. Метод касательных.
- •Требуются решить уравнение: (1), другими словами – найти нули функции, т.Е. Такие , которые обращают уравнение (1) в тождество.
- •20.Скалярное нелинейное уравнение. Комбинированный метод хорд и касательных.
- •Требуются решить уравнение: (1), другими словами – найти нули функции, т.Е. Такие , которые обращают уравнение (1) в тождество.
- •21. Скалярное нелинейное уравнение. Метод простых итераций.
- •Требуются решить уравнение: (1), другими словами – найти нули функции, т.Е. Такие , которые обращают уравнение (1) в тождество.
- •22. Система скалярных нелинейных уравнений. Метод простых итераций.
- •Если обозначить
- •23. Система скалярных нелинейных уравнений. Метод наискорейшего спуска.
- •24. Метод скорейшего спуска решения система линейных алгебраических уравнений. Пусть дана система линейных алгебраических уравнений:
32 Квадратурные формулы Ньютона-Котеса.
Рассмотрим интервал на котором построена равномерная сетка узлов и известны значения функции в этих узлах:
Тогда где
Так как система узлов равномерна, то
Следовательно
Отсюда получим
Коэффициенты называются квадратурными коэффициентами Ньютона-Котеса.
Свойства коэффициентов Ньютона-Котеса.
Коэффициенты Ньютона-Котеса для узлов равноудаленных от концов отрезка, равны:
Сумма всех коэффициентов Ньютона-Котеса на равна 1:
Доказательство: Возьмем в формуле (1) . Тогда ч.т.д.
При и среди коэффициентов Ньютона-Котеса существуют отрицательные коэффициенты. Как правило, квадратичные формулы строятся с малым числом n т.к. большее число и ведет к росту погрешности.
33 Квадратурные формулы наивысшей степени точности.
Их так же называют
формулами Гаусса. Мы заменяем интеграл
квадратурной формулой:
Интерполирование
функции
![]() ,
причем
,
причем
![]() когда
когда
![]() - множество многочленов степени не выше
.Степенью
точности квадратурной формулы называется
такая степень многочлена, при подстановке
которого вместо функции
в интеграл получится точное равенство
в квадратурной формуле или остаточный
член равен нулю. Таким образом, степень
точности квадратурной формулы равна
на
- множество многочленов степени не выше
.Степенью
точности квадратурной формулы называется
такая степень многочлена, при подстановке
которого вместо функции
в интеграл получится точное равенство
в квадратурной формуле или остаточный
член равен нулю. Таким образом, степень
точности квадратурной формулы равна
на
![]() узле.
узле.
Замечание. Без ограничения общности рассуждений будем считать, что узлы нумеруются от 1 до n.
Тогда имеем для
квадратурных формул
узлов и
![]() - степень точности.
- степень точности.
Пусть необходимо
найти
![]() .
Как правило, сложно построенные функции
или функции, имеющие особенности на
,
стремятся представить в виде произведения:
.
Как правило, сложно построенные функции
или функции, имеющие особенности на
,
стремятся представить в виде произведения: ![]()
где
![]() - достаточно гладкая функция,
- достаточно гладкая функция,
![]() - весовая функция, которая вбирает в
себя особенности функции
.
Тогда заменим
- весовая функция, которая вбирает в
себя особенности функции
.
Тогда заменим
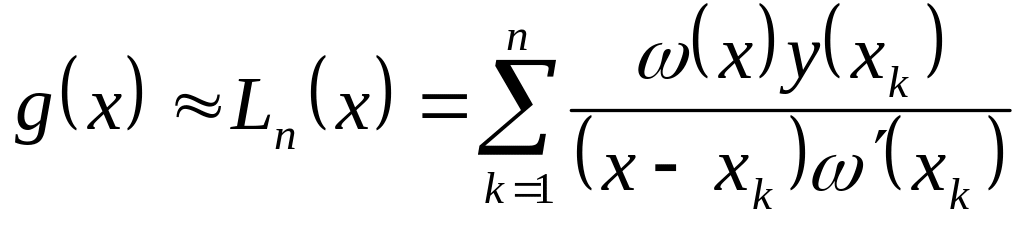

Оказывается, равномерный способ распределения узлов интегрирования для повышения степени точности не является удовлетворительным, т.е. путем выбора (специального) узлов интегрирования можно повысить степень точности.
Th:
Для того чтобы квадратурная формула
имела наивысшую степень точности
![]() ,
где
- число узлов интегрирования, необходимо
и достаточно, чтобы:
,
где
- число узлов интегрирования, необходимо
и достаточно, чтобы:
квадратурная формула была формулой интерполяционного типа, т.е.
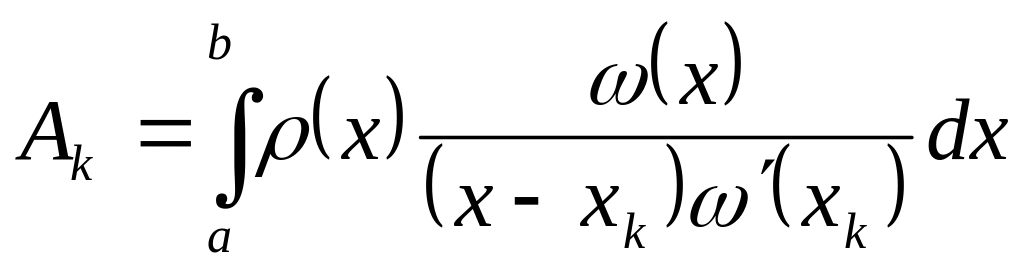
2.многочлен
![]() был ортогонален с весом
на отрезке
любому многочлену степени не выше, чем
,
т.е.
был ортогонален с весом
на отрезке
любому многочлену степени не выше, чем
,
т.е.
![]() ,
где
,
где
![]() - многочлен степени не выше
.
- многочлен степени не выше
.
Доказательство:
Необходимость.
Первое свойство,
очевидно, выполняется из выкладок. Пусть
квадратурная формула точна, докажем
выполнение второго свойства: Пусть
степень многочлена![]() -
,
а
-
,
тогда степень многочлена
-
,
а
-
,
тогда степень многочлена
![]() будет
будет
![]() ,
так как
,
так как
![]() .
.
Достаточность. Пусть имеется свойство ортогональности. Докажем, что квадратурная формула будет точной.
Возьмем функцию
- многочлен степени не выше чем
.
Тогда ![]() ,
,
где
![]() ,
,![]() - многочлены степени меньше
.Тогда
- многочлены степени меньше
.Тогда
![]() ч.т.д. Рассмотрим
второе условие – условие
ортогональности:
. Пусть
многочлен
имеет степень
ч.т.д. Рассмотрим
второе условие – условие
ортогональности:
. Пусть
многочлен
имеет степень
![]() ,
так как равенство выполняется для
многочлена степени
,
то оно должно выполнятся для элементарных
многочленов
,
так как равенство выполняется для
многочлена степени
,
то оно должно выполнятся для элементарных
многочленов
![]() ,
т.е.
,
т.е. ![]() (*)
(*)
Это есть система
нелинейных
![]() уравнений относительно неизвестных
значений узлов многочлена
,
которых
штук. Для однозначной разрешимости
необходимо чтобы число уравнений было
равно числу неизвестных, т.е.
уравнений относительно неизвестных
значений узлов многочлена
,
которых
штук. Для однозначной разрешимости
необходимо чтобы число уравнений было
равно числу неизвестных, т.е.
![]() ,
следовательно
,
следовательно
![]() .
С учетом степени самого члена
мы имеем, что степень
-
.
.
С учетом степени самого члена
мы имеем, что степень
-
.
Для точности рассуждений требуется показать существование и единственность такого многочлена , что его корни все различны, действительны и лежат внутри отрезка .
Докажем это.
Потребуем, чтобы
функция
была знакопостоянной, т.е.
![]() .
.
Выпишем СЛАУ (*):
Т.к.
![]() ,
то
,
то
![]()
![]()
![]()
это система неоднородных линейных уравнений относительно
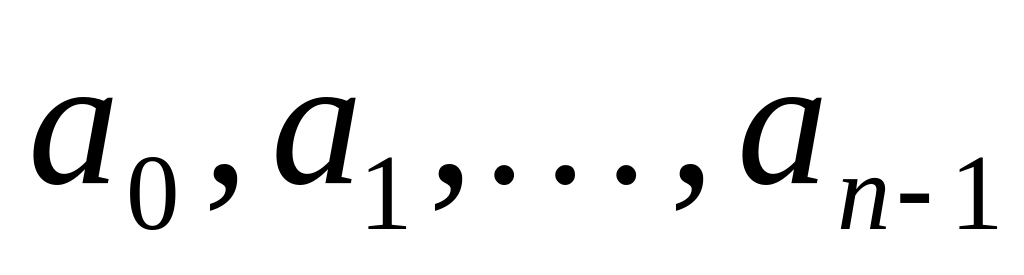 .
Она имеет единственное решение, когда
однородная система
.
Она имеет единственное решение, когда
однородная система
![]() , т.е.
, т.е. ![]()
имеет только
тривиальное решение. Покажем это. Для
этого умножим каждое уравнение системы
на соответствующий коэффициент
![]() и просуммируем по
и просуммируем по
![]() .
.
![]()
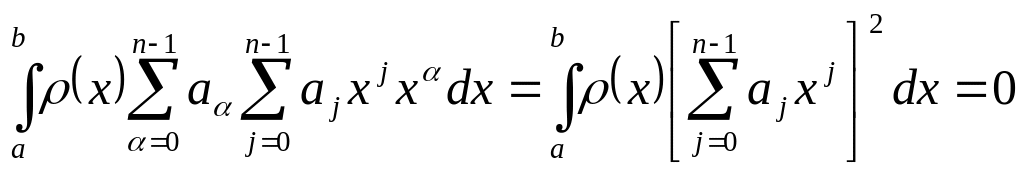
Т.к.
![]() и
и
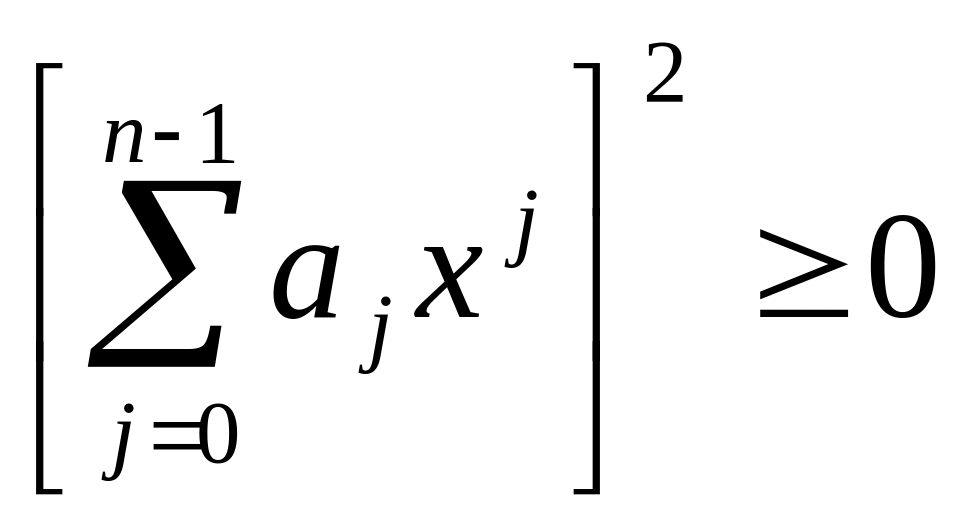 ,
то для любого
,
то для любого
![]() ,
,
![]() .
.
Следовательно, мы доказали, что однородное СЛАУ имеет только тривиальное решение. Это означает, что неоднородное система имеет единственное решение, т.е. многочлен ортогонален с весом любому многочлену степени меньше существует и единственен.
Покажем, что его корни лежат внутри и их ровно штук.
Пусть многочлен имеет действительных корней лежащих на , нечетной кратности:
![]() соответственно
их кратности:
соответственно
их кратности: ![]()
Так как степень
равна
,
то
![]() .
.
Тогда
![]() ,
где
,
где
![]() - многочлен степени меньше
,
знакопостоянной на
.
Найдем
- многочлен степени меньше
,
знакопостоянной на
.
Найдем
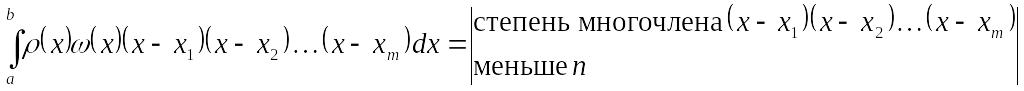
Допустим противное,
т.е. что
![]() .
Тогда из последнего выражения получим
следующее:
.
Тогда из последнего выражения получим
следующее:
![]() ,
,
![]() ,
,
так как ортогонален с весом любому многочлену степени меньше .
Но с другой стороны
интеграл отличен от нуля, поэтому наше
предположение неверно. Значит
![]()
