
- •1 Метод Гаусса (lu-разложений).
- •2 Нахождения определителя матрицы методом Гаусса.
- •3 Уточнение решения полученного методом Гаусса.
- •4 Нахождение элементов обратной матрицы методом Гаусса.
- •Пусть дана слау
- •29 Квадратурные формулы Ньютона-Котеса.
- •Свойства коэффициентов Ньютона-Котеса.
- •30 Формула трапеций.
- •Оценим остаточный член:
- •31 Формула Симпсона ( параболы).
- •32 Квадратурные формулы Ньютона-Котеса.
- •Свойства коэффициентов Ньютона-Котеса.
- •33 Квадратурные формулы наивысшей степени точности.
- •Свойства.
- •34 Интегрирование быстроосциллирующих функций.
- •Существование и единственность задачи Коши дается в теореме Пикара.
- •36 Метод Пикара.
- •37 Метод Эйлера.
- •Т.Е. Хоть и не сказано о том, что выполняется условие Липшица, но зато ограничено, и мы можем оценить | |l.
- •48 Метод правой прогонки.
- •49. Метод левой прогонки.
- •51 Метод Либмана.
- •Рассмотрим уравнение эллиптического типа – уравнение Пуассона:
- •53 Метод сеток для решения уравнений параболического типа.
- •8. Итерационные методы решение систем линейно-алгебраических уравнений.
- •Пусть дана слау
- •9. Метод простых итераций для решения линейно-алгебраических уравнений.
- •Нормы векторов и матрицы.
- •11. Метод Зейделя. Условия сходимости метода
- •1.Теорема об lu-разложении кв. Матрицы. Метод Гаусса решения слау.
- •Теорема: (об lu – разложений матрицы).
- •Методика решения.
- •2. Теорема об lu-разложении кв. Матрицы. Нахождения определителя матрицы методом Гаусса. Теорема: (об lu – разложений матрицы).
- •Нахождения определителя матрицы методом Гаусса
- •3.Уточнение решения полученного методом Гаусса.
- •4. Нахождение элементов обратной матрицы методом Гаусса.
- •Пусть дана слау
- •14. Проблема собственных значений. Метод Данилевского.
- •Метод а.М. Данилевского
- •Теорема: Преобразование подобия не изменяет собственных значений матрицы.
- •15. Проблема собственных значений. Степенной метод .
- •Степенной метод.
- •Обозначим соответствующие собственные векторы через
- •Степенной метод имеет задачу нахождения пары:
- •17. Скалярное нелинейное уравнение.Метод половинного деления (дихотомии).
- •Требуются решить уравнение: (1), другими словами – найти нули функции, т.Е. Такие , которые обращают уравнение (1) в тождество.
- •Метод половинного деления
- •12.Метод вращения решения слау
- •18.Скалярное нелинейное уравнение. Метод хорд.
- •Требуются решить уравнение: (1), другими словами – найти нули функции, т.Е. Такие , которые обращают уравнение (1) в тождество.
- •18. Скалярное нелинейное уравнение. Метод касательных.
- •Требуются решить уравнение: (1), другими словами – найти нули функции, т.Е. Такие , которые обращают уравнение (1) в тождество.
- •20.Скалярное нелинейное уравнение. Комбинированный метод хорд и касательных.
- •Требуются решить уравнение: (1), другими словами – найти нули функции, т.Е. Такие , которые обращают уравнение (1) в тождество.
- •21. Скалярное нелинейное уравнение. Метод простых итераций.
- •Требуются решить уравнение: (1), другими словами – найти нули функции, т.Е. Такие , которые обращают уравнение (1) в тождество.
- •22. Система скалярных нелинейных уравнений. Метод простых итераций.
- •Если обозначить
- •23. Система скалярных нелинейных уравнений. Метод наискорейшего спуска.
- •24. Метод скорейшего спуска решения система линейных алгебраических уравнений. Пусть дана система линейных алгебраических уравнений:
Метод половинного деления
Пусть
дано уравнение f(x)=0
и отделен простой корень x*
т.е. найден такой отрезок [a;b],
что x*[a;b],
и на концах отрезка функция имеет
значения, противоположные по знаку.
Процедура уточнения положения корня
заключается в построении последовательности
вложенных друг в друга отрезков, каждый
из которых содержит корень уравнения.
Отрезок
делиться пополам точкой
,
где
![]() .
Определяется, на каком интервале лежит
корень, на
.
Определяется, на каком интервале лежит
корень, на
![]() или на
или на
![]() ,
т.е. определяется знак значения
,
т.е. определяется знак значения
![]() и знаки произведений
и знаки произведений
![]() и
и
![]() .
Если
.
Если
![]() ,
то на интервале
находиться корень. Если же
,
то на интервале
находиться корень. Если же
![]() - то корень на
.
Интервал сужается, и точка
переименовывается в точку
- то корень на
.
Интервал сужается, и точка
переименовывается в точку
![]() и процесс продолжается, т.е.
и процесс продолжается, т.е.
![]() ,
,
![]() ,
,
![]() ,
,
…
![]()
![]()
Имеем замкнутые
вложенные отрезки
![]() .
По теореме Кантора о системе замкнутых
вложенных друг в друга отрезках с
.
По теореме Кантора о системе замкнутых
вложенных друг в друга отрезках с
![]() ,
существует единственная точка,
принадлежащая всем отрезкам, которая
и будет точным решением уравнения(1).
,
существует единственная точка,
принадлежащая всем отрезкам, которая
и будет точным решением уравнения(1).![]()
![]()
левые концы отрезков
![]() образуют неубывающую ограниченную
последовательность, а правые концы
образуют неубывающую ограниченную
последовательность, а правые концы
![]() - не возрастающую последовательность.
По теореме и та и другая последовательности
имеют предел.
- не возрастающую последовательность.
По теореме и та и другая последовательности
имеют предел.
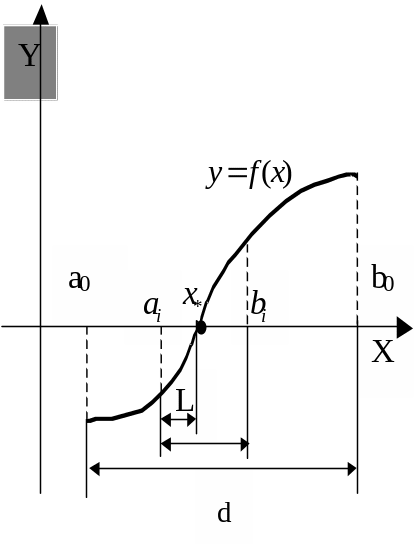 Метод
половинного деления не требует
дифференцируемости функции.
Метод
половинного деления не требует
дифференцируемости функции.
Скорость сходимости
этого метода есть скорость сходимости
геометрической прогрессии со знаменателем
![]() .
Итерационный процесс прекращается,
когда
.
Итерационный процесс прекращается,
когда
![]() .Мы
попадаем в интервал длины
.
Любая точка этого интервала можно
принять за решения. Но точность, как
правило, увеличивается, если взять
середину этого отрезка.
.Мы
попадаем в интервал длины
.
Любая точка этого интервала можно
принять за решения. Но точность, как
правило, увеличивается, если взять
середину этого отрезка.
Метод является достаточно универсальным. На функцию кроме непрерывности и разности знаков на концах не накладываются дополнительные условия. Для увеличения скорости сходимости метода интервал делиться на большее количество частей.
+
+
+![]()
![]()
![]()
![]()
![]()













12.Метод вращения решения слау
В решении системы методом Гаусса, коэффициенты системы могут возрастать.
Рассмотрим систему Ax=f, т.е.
a 11x1+a12x2+…+a1nxn=f1
*k1
*(-k2)
11x1+a12x2+…+a1nxn=f1
*k1
*(-k2)
a21x1+a22x2+…+a2nxn=f2 *k2 *k1
…………………..
an1x1+a2nx2+…+annxn=fn
Сложим, получим
a 12 a 1n f1
(k1a1+k2a21)x1+(k1a12+k2a22)x2+…+(k1a1n+k2a2n)xn=(k1f1+k2f2)
(-k2a11+k1a21)+…+(-k2a1n+k1a2n)xn= f2
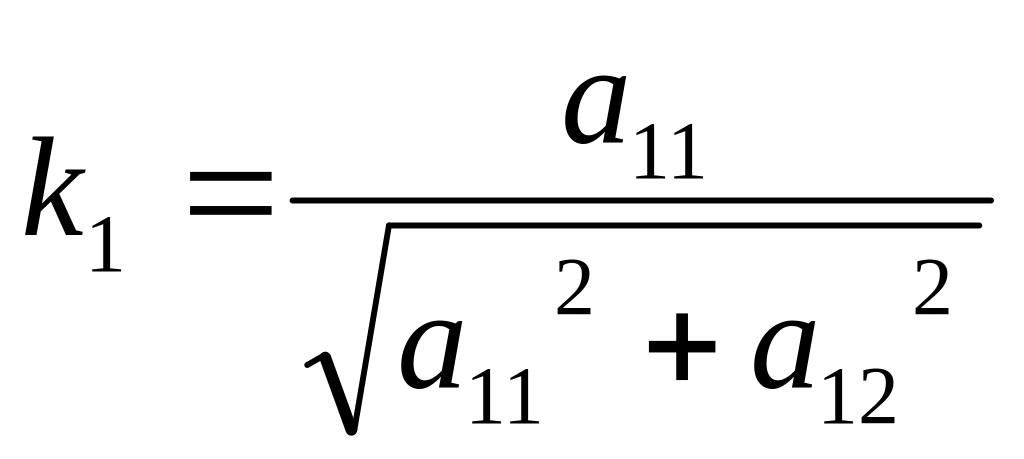
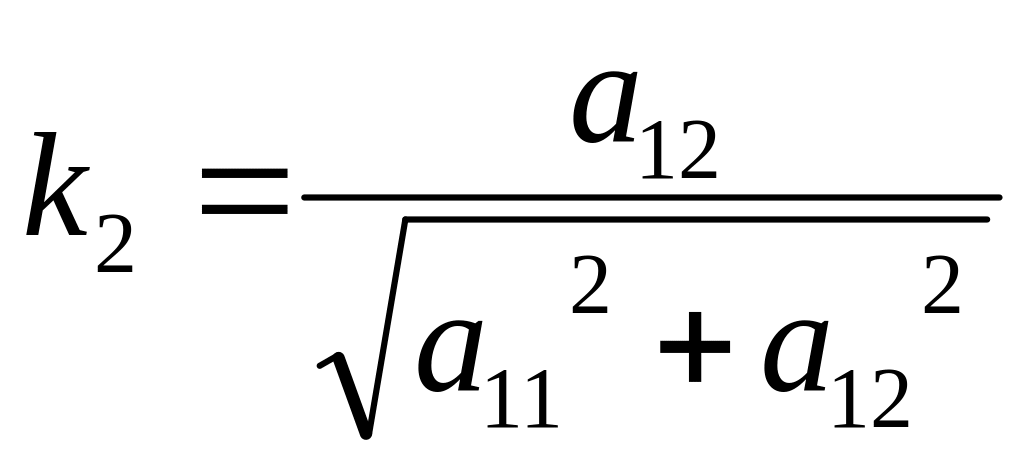
18.Скалярное нелинейное уравнение. Метод хорд.
Р ассмотрим функцию одной переменной f(x).
Требуются решить уравнение: (1), другими словами – найти нули функции, т.Е. Такие , которые обращают уравнение (1) в тождество.
Корней может быть либо:
1)нечетное множество;
2)счетное множество;
3)конечное множество.
Поэтому, как правило, оговаривается интервал, в котором ищутся корни.
Функция имеет единственный корень на отрезке когда она:
1)непрерывна на отрезке , т.е. ;
2)на концах имеет значение разных знаков, т.е.
3)строго монотонна (для дифференцируемых функций строгая монотонность эквивалентна знакопостоянству производной).
Прежде чем решить задачу (1) требуется отделить корни, т.е. указать такие интервалы , каждый из которых содержит единственный корень.
Если функция - достаточно простая функция, то отделение корней можно осуществить графически. Если же вид функции сложный или функция не задана явно, то отделение корней осуществляется программно.
Для отделения корней поступают следующим образом:
задается некоторый шаг
ищутся отрезки длины изменения знака функции.
Будем считать, что корни уравнения (1) отделены и будем рассматривать отрезок , где существует единственный корень.
Метод хорд
Потребуется , чтобы
![]() - была дважды дифференцируема на
- была дважды дифференцируема на
![]() .
.
Рассмотрим 4 случая различающиеся знаком 1-ой и 2-ой производной.
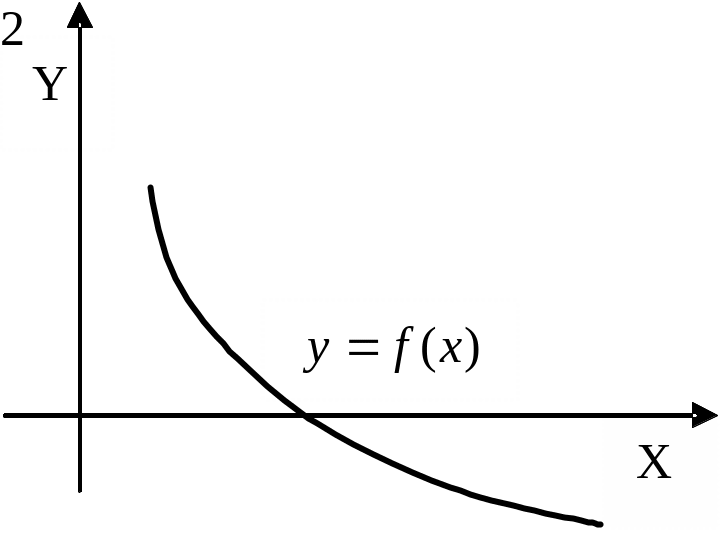
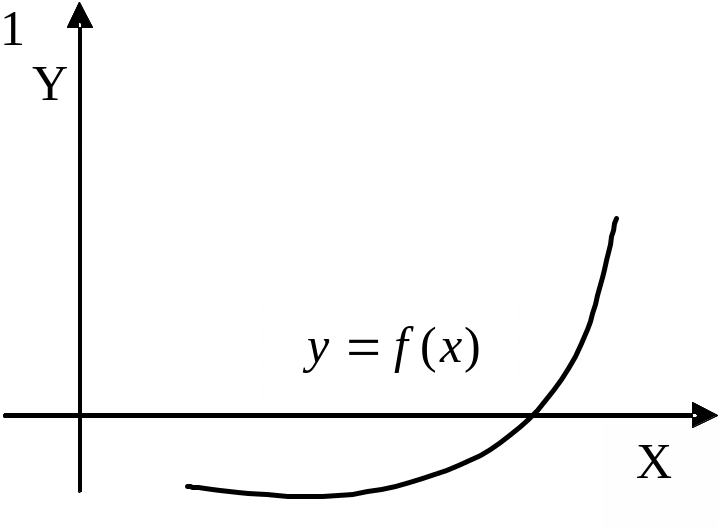
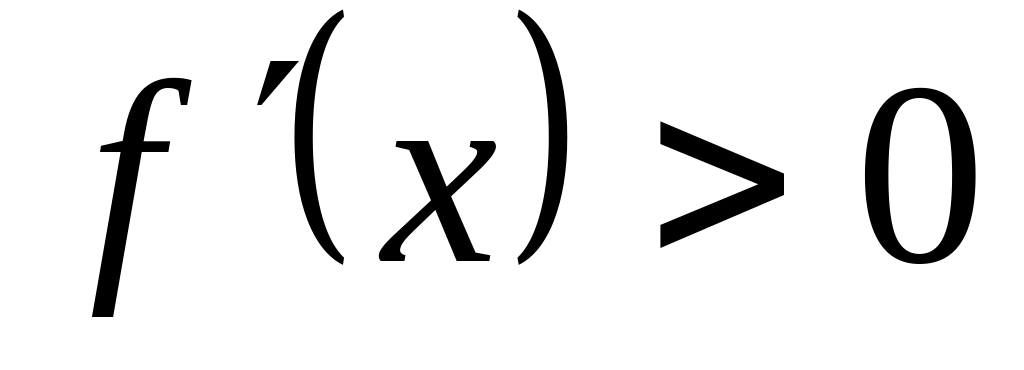 ,
,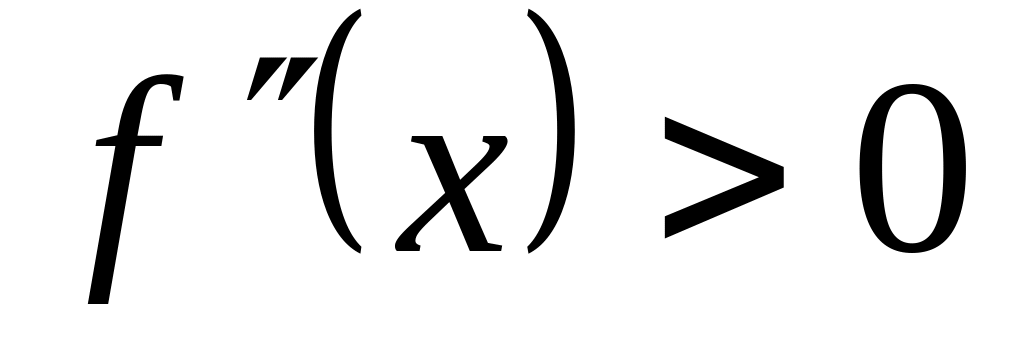
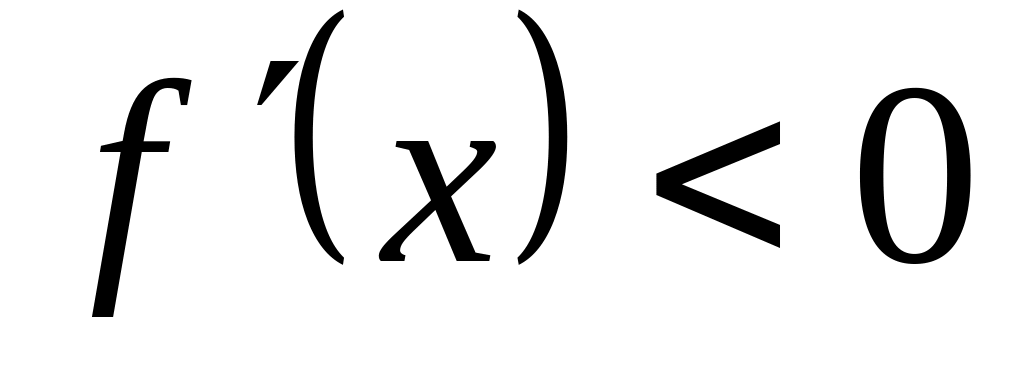 ,
,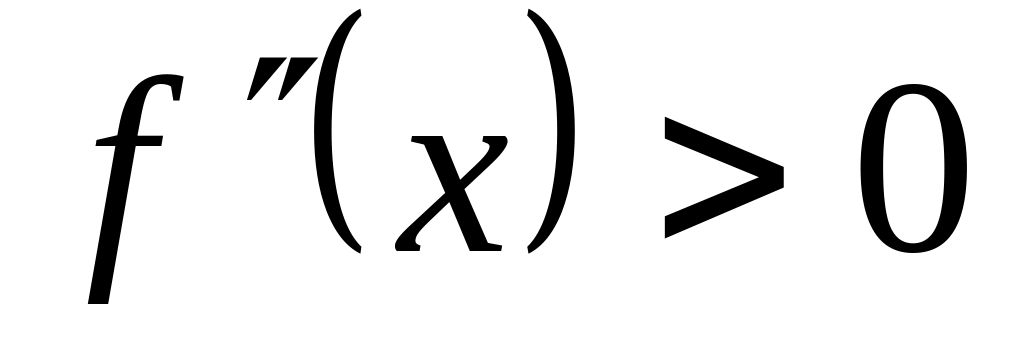
,
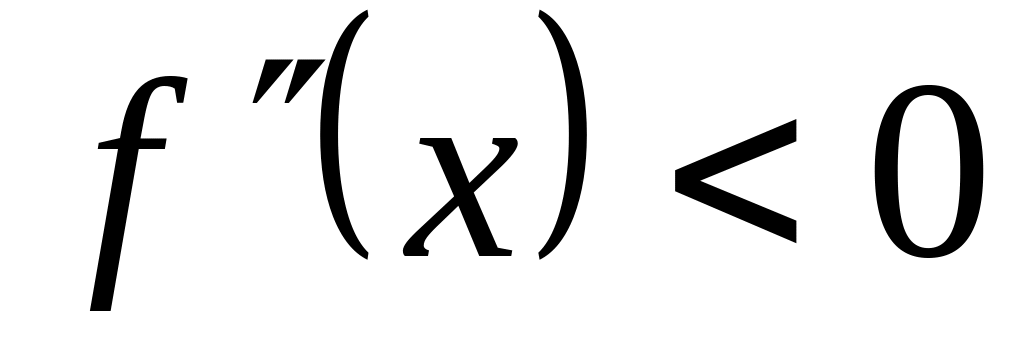
,
Р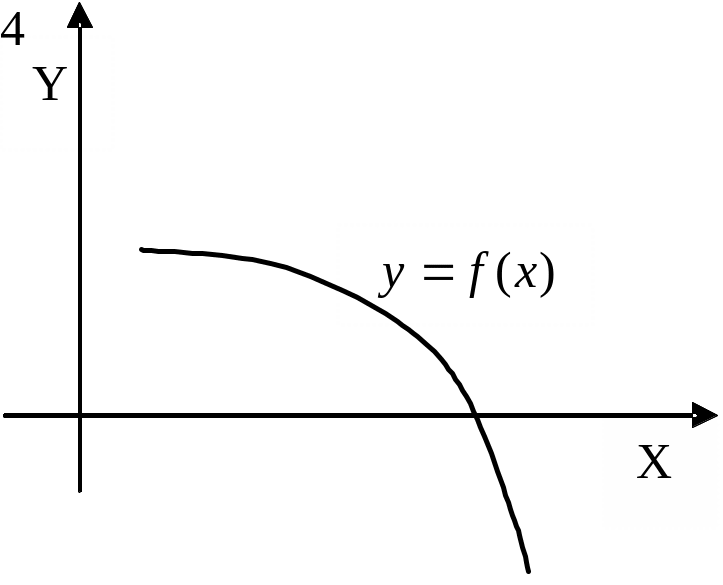
 ассмотрим
2-ой случай.
ассмотрим
2-ой случай.
2. ,
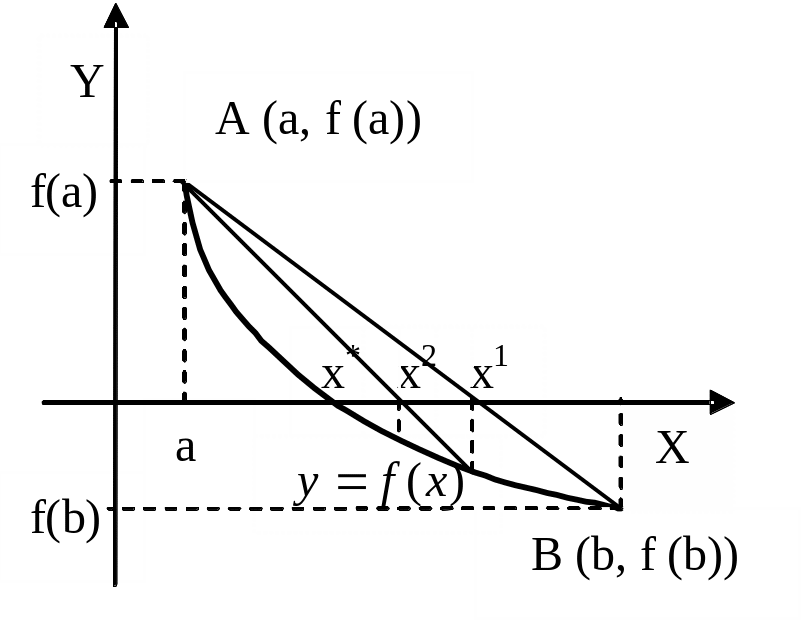
Требуется найти
уравнение прямой проходящей через две
точки,
![]() и
и
![]() ,
и найти координаты точки пересечения
этой прямой с осью ОX.
,
и найти координаты точки пересечения
этой прямой с осью ОX.
1.Найдем прямую проходящую через точки А и .B
![]()
Выразим точку пересечения прямой с осью OX из уравнения прямой:
![]()
![]()
Если
![]() тогда
тогда
![]()
- первое приближение через нулевую точку x0 справа.
Аналогично, строим
прямую через точки
и
![]() .Находим
точку пересечения построенной прямой
с осью ОХ и выражаем через построенное
уравнение. В итоге получим второе
приближение. Аналогичными построениями
получим
.Находим
точку пересечения построенной прямой
с осью ОХ и выражаем через построенное
уравнение. В итоге получим второе
приближение. Аналогичными построениями
получим
![]() -ое
приближение справа.
-ое
приближение справа.
![]() (*)
(*)
Если взять в качестве нулевой точки точку , то получим соответствующее приближение справа:
![]() (**).
(**).
Для установления неподвижности точки применяется следующий критерий:
Критерий
неподвижности точки: Точка будет
неподвижной тогда и только тогда, когда
![]() ,
где t=а или t=b
Если
,
где t=а или t=b
Если
![]() - тогда конец,
является неподвижным и применяется
формула (**), а если
- тогда конец,
является неподвижным и применяется
формула (**), а если
![]() ,
то
неподвижный конец и применяется формула
(*).
,
то
неподвижный конец и применяется формула
(*).
Условие
![]() является условием выхода из итерационного
процесса.
является условием выхода из итерационного
процесса.
