
- •1 Метод Гаусса (lu-разложений).
- •2 Нахождения определителя матрицы методом Гаусса.
- •3 Уточнение решения полученного методом Гаусса.
- •4 Нахождение элементов обратной матрицы методом Гаусса.
- •Пусть дана слау
- •29 Квадратурные формулы Ньютона-Котеса.
- •Свойства коэффициентов Ньютона-Котеса.
- •30 Формула трапеций.
- •Оценим остаточный член:
- •31 Формула Симпсона ( параболы).
- •32 Квадратурные формулы Ньютона-Котеса.
- •Свойства коэффициентов Ньютона-Котеса.
- •33 Квадратурные формулы наивысшей степени точности.
- •Свойства.
- •34 Интегрирование быстроосциллирующих функций.
- •Существование и единственность задачи Коши дается в теореме Пикара.
- •36 Метод Пикара.
- •37 Метод Эйлера.
- •Т.Е. Хоть и не сказано о том, что выполняется условие Липшица, но зато ограничено, и мы можем оценить | |l.
- •48 Метод правой прогонки.
- •49. Метод левой прогонки.
- •51 Метод Либмана.
- •Рассмотрим уравнение эллиптического типа – уравнение Пуассона:
- •53 Метод сеток для решения уравнений параболического типа.
- •8. Итерационные методы решение систем линейно-алгебраических уравнений.
- •Пусть дана слау
- •9. Метод простых итераций для решения линейно-алгебраических уравнений.
- •Нормы векторов и матрицы.
- •11. Метод Зейделя. Условия сходимости метода
- •1.Теорема об lu-разложении кв. Матрицы. Метод Гаусса решения слау.
- •Теорема: (об lu – разложений матрицы).
- •Методика решения.
- •2. Теорема об lu-разложении кв. Матрицы. Нахождения определителя матрицы методом Гаусса. Теорема: (об lu – разложений матрицы).
- •Нахождения определителя матрицы методом Гаусса
- •3.Уточнение решения полученного методом Гаусса.
- •4. Нахождение элементов обратной матрицы методом Гаусса.
- •Пусть дана слау
- •14. Проблема собственных значений. Метод Данилевского.
- •Метод а.М. Данилевского
- •Теорема: Преобразование подобия не изменяет собственных значений матрицы.
- •15. Проблема собственных значений. Степенной метод .
- •Степенной метод.
- •Обозначим соответствующие собственные векторы через
- •Степенной метод имеет задачу нахождения пары:
- •17. Скалярное нелинейное уравнение.Метод половинного деления (дихотомии).
- •Требуются решить уравнение: (1), другими словами – найти нули функции, т.Е. Такие , которые обращают уравнение (1) в тождество.
- •Метод половинного деления
- •12.Метод вращения решения слау
- •18.Скалярное нелинейное уравнение. Метод хорд.
- •Требуются решить уравнение: (1), другими словами – найти нули функции, т.Е. Такие , которые обращают уравнение (1) в тождество.
- •18. Скалярное нелинейное уравнение. Метод касательных.
- •Требуются решить уравнение: (1), другими словами – найти нули функции, т.Е. Такие , которые обращают уравнение (1) в тождество.
- •20.Скалярное нелинейное уравнение. Комбинированный метод хорд и касательных.
- •Требуются решить уравнение: (1), другими словами – найти нули функции, т.Е. Такие , которые обращают уравнение (1) в тождество.
- •21. Скалярное нелинейное уравнение. Метод простых итераций.
- •Требуются решить уравнение: (1), другими словами – найти нули функции, т.Е. Такие , которые обращают уравнение (1) в тождество.
- •22. Система скалярных нелинейных уравнений. Метод простых итераций.
- •Если обозначить
- •23. Система скалярных нелинейных уравнений. Метод наискорейшего спуска.
- •24. Метод скорейшего спуска решения система линейных алгебраических уравнений. Пусть дана система линейных алгебраических уравнений:
1 Метод Гаусса (lu-разложений).
Теоретической основой метода Гаусса является следующее разложение:
Теорема: (об
LU – разложений матрицы).
Любая квадратная невырожденная матрица
А, у которой главные миноры отличные от
нуля, может быть представлена в виде
произведения двух матриц А=В![]() С,
где
С,
где
В – нижне-треугольная матрица (лево треугольная матрица);
С – верхне-треугольная матрица (право треугольная матрица).
Причём это разложение единственно с точностью до диагональных членов.
Определение: Если мы зафиксируем элементы диагонали, то разложение будет единственно, такое разложение называется разложением с точностью до диагональных членов.
Берут в качестве фиксированных элементов на диагонали обычно 1.
Так
как разложение матрицы А представляется
в виде произведения, то уравнение (1)
преобразуется:
![]() (2).
(2).
![]()
![]()
Определение: Разложение матрицы А в разложение В и С называется прямым ходом метода Гаусса.
Определение: Нахождение вектора х по (3) и (4) называется обратным ходом метода Гаусса. Решим уравнение (3):
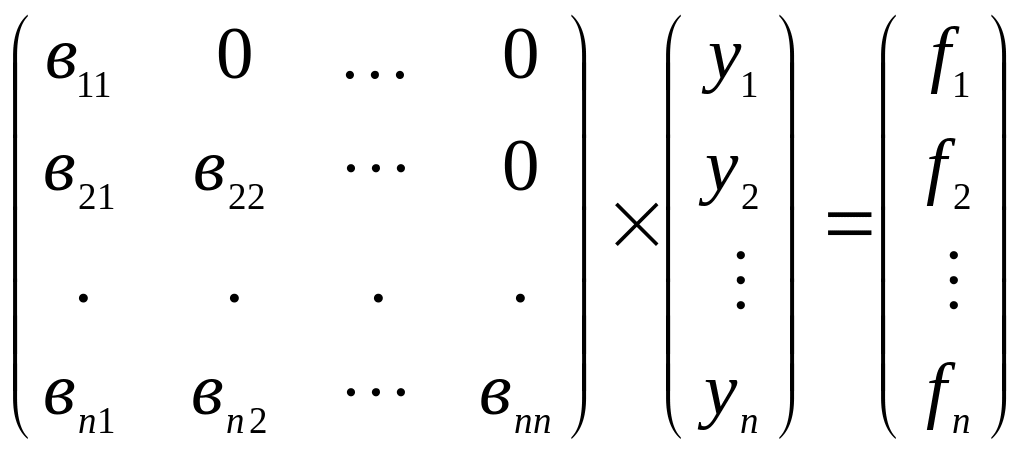 для
этого решим систему уравнений:
для
этого решим систему уравнений:
![]()
Решим уравнение (4):
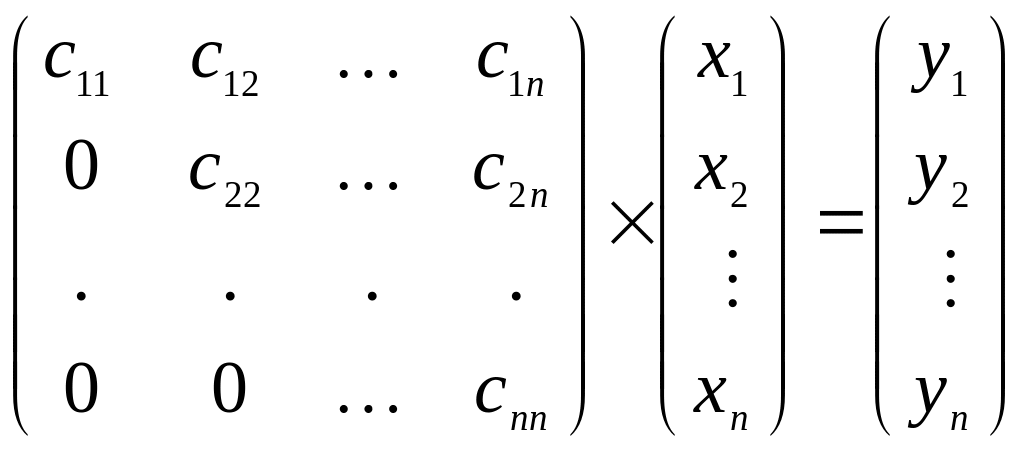
![]()
Пусть имеет место разложение, т.е.
А=В С или
 Тогда:
Тогда:
![]()
 ,
то
,
то
![]()
 ,
то
,
то
![]()
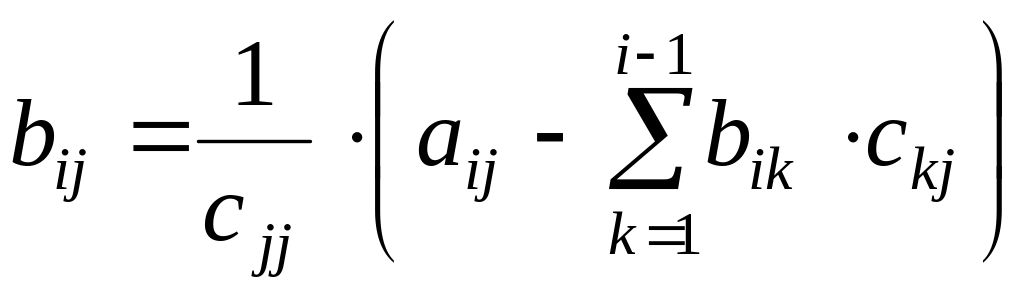 ,
(7)
,
(7)
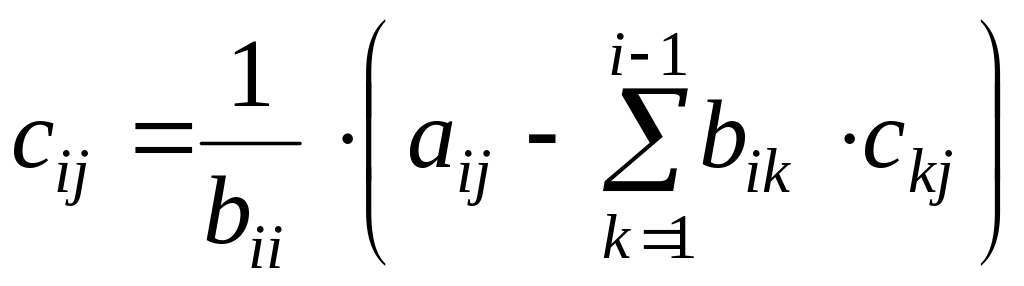 ,
,
![]() (8)
(8)
Снятие неопределённости в (7) и (8) следует из правильного порядка вычисления этих формул.
Счёт
по формулам ведётся следующим образом:
с помощью пар индексов
![]() счёт ведётся по строкам
обеих матриц сразу.
счёт ведётся по строкам
обеих матриц сразу.
2 Нахождения определителя матрицы методом Гаусса.
Согласно теореме об LU разложении: А=В*С, по свойству определителя
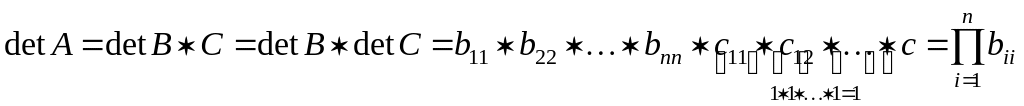
3 Уточнение решения полученного методом Гаусса.
Пусть
![]() приближённое решение уравнения:
приближённое решение уравнения: ![]() (1)
(1)
где
погрешность находится по следующей
формуле:
![]() ,
,
а
невязка:
![]() .
.
Найдем
взаимосвязь между невязкой
![]() и погрешностью
и погрешностью
![]() .
Для этого подействуем оператором А на
погрешность
,
т.е.
.
Для этого подействуем оператором А на
погрешность
,
т.е.
![]() т.е.
т.е.
![]() .
.
Пусть
для любой правой части
![]() в (1) имеет место, следующее неравенство:
в (1) имеет место, следующее неравенство:
![]() .
.
Построим итерационный процесс уточнения. Начальное приближение:
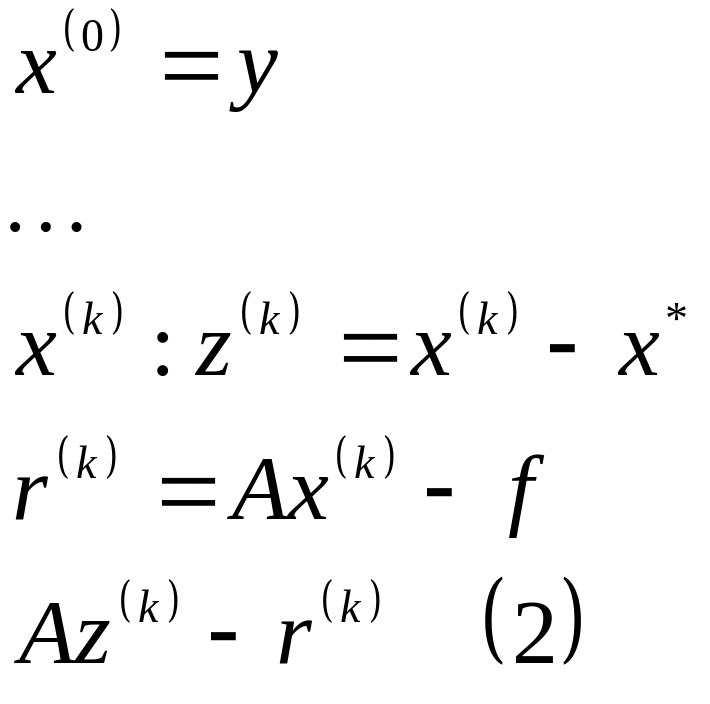
Для
любого k
найдём
![]() .
.
![]() - погрешность.
- погрешность.
Найдём
![]() -ое
приближение:
-ое
приближение:
![]() (3)
(3)
и
докажем что
![]() -ое
приближение будет наиболее ближе к
точному
-ое
приближение будет наиболее ближе к
точному
![]() ,
чем
,
чем
![]() -тое
-тое
приближение.
Док – во:
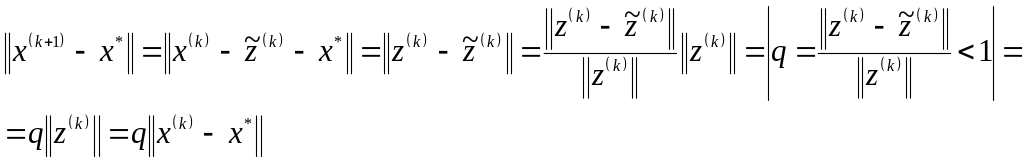
т.е.
приближение ![]() ближе к точному решению
ближе к точному решению
![]() ,
чем
,
чем
![]() .
.
ч.т.д.
Таким
образом, решая систему (1) с правой частью
![]() методом Гаусса. Решение обозначаем за
методом Гаусса. Решение обозначаем за
![]() .
Находиться невязка
.
Находиться невязка
![]() ,
решается система
,
решается система
![]() и находиться
и находиться
![]() .
.
Из равенства (3) определяем новое приближение. Процедура выполняется до выполнения условия:
![]() .
.
Замечание.
Уточнение иногда производят по упрощенной схеме. Задаются системы векторов невязок с убывающей нормой.
4 Нахождение элементов обратной матрицы методом Гаусса.
Определение. Ненулевая матрица А называется обратимой, если существует матрица А-1, называемая обратной и выполнено условие:
![]()
Пусть Х – обратная матрица. Тогда ![]() (*)
(*)
где
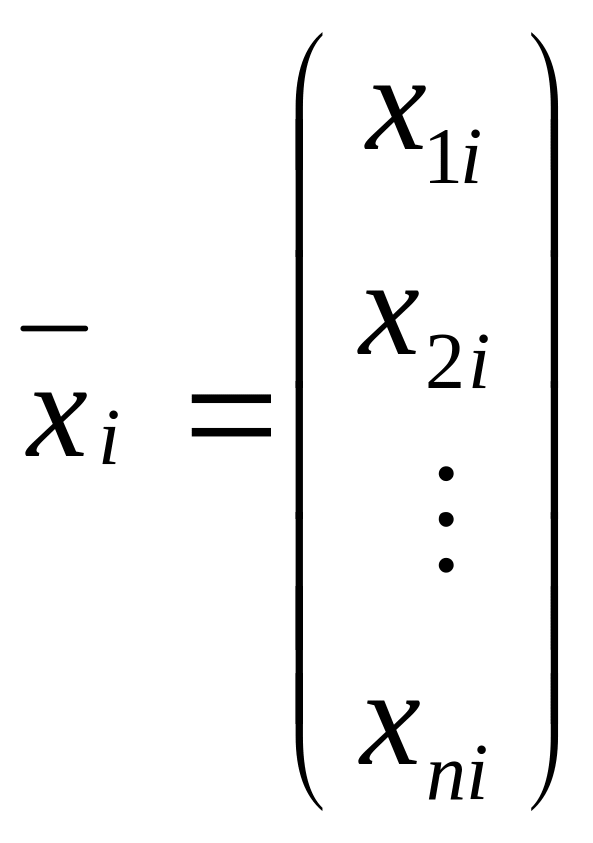 ,
и
,
и
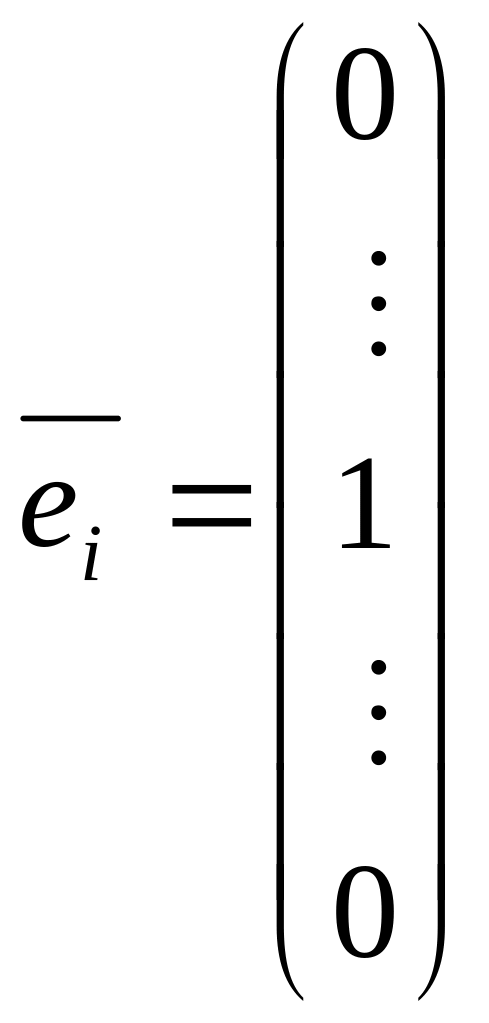 .
.
Тогда уравнение (*) можно представить следующим образом:
![]() .(**)
.(**)
частями
Правило:
Подставляя
различные k
в (**) мы получим k-ый
столбец. Затем запишем матрицу состоящую
из
![]() .
Таким образом, нужно решить n
СЛАУ, с различными правыми частями , где
в качестве столбца свободных членов
поочередно берутся столбцы единичной
матрицы. Разложение матрицы А достаточно
сделать один раз.
.
Таким образом, нужно решить n
СЛАУ, с различными правыми частями , где
в качестве столбца свободных членов
поочередно берутся столбцы единичной
матрицы. Разложение матрицы А достаточно
сделать один раз.
5 Метод квадратного корня, решения систем линейно-алгебраических уравнений с эрмитовыми матрицами.
