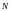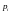Эффективное кодирование. Коды Шеннона-Фано.
Сущность кодов заключается в том, что они неравномерные, то есть с неодинаковым числом разрядов, причем длина кода обратно пропорциональна вероятности его появления. Еще одна замечательная особенность эффективных кодов – они не требуют разделителей, то есть специальных символов, разделяющих соседние кодовые комбинации. Это достигается при соблюдении простого правила: более короткие коды не являются началом более длинных. В этом случае сплошной поток двоичных разрядов однозначно декодируется, поскольку декодер обнаруживает вначале более короткие кодовые комбинации. Эффективные коды долгое время были чисто академическими, но в последнее время успешно используются при формировании баз данных, а также при сжатии информации в современных модемах и в программных архиваторах [39].
Ввиду неравномерности вводят среднюю длину кода. Средняя длина – математическое ожидание длины кода:
|
(2.22) |
.Здесь
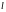– длина
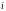-той
кодовой комбинации;
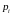– ее вероятность;
– число различных комбинаций. Особенностью
эффективных кодов является то, что
средняя длина кода приближается к
энтропии источника:
|
(2.23) |
,
причем,
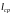стремится к
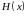сверху (то есть
).
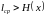Выполнение условия (2.23) усиливается при увеличении .
Существует две разновидности эффективных кодов: Шеннона-Фано и Хафмана. Рассмотрим их получение на примере. Предположим, вероятности символов в последовательности имеют значения, приведенные в таблице 2.1.
Таблица 2.1
Вероятности символов
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0,1 |
0,2 |
0,1 |
0,3 |
0,05 |
0,15 |
0,03 |
0,02 |
0,05 |
Символы ранжируются, то есть представляются в ряд по убыванию вероятностей. После этого по методу Шеннона-Фано периодически повторяется следующая процедура: вся группа событий делится на две подгруппы с одинаковыми (или примерно одинаковыми) суммарными вероятностями. Процедура продолжается до тех пор, пока в очередной подгруппе не останется один элемент, после чего этот элемент устраняется, а с оставшимися указанные действия продолжаются. Это происходит до тех пор, пока в последних двух подгруппах не останется по одному элементу. Продолжим рассмотрение нашего примера, которое сведено в таблице 2.2.
Т
аблица
2.2.
Кодирование по методу Шеннона-Фано
|
|
1 |
2 |
3 |
4 |
5 |
|
4 |
0,3 |
|
I |
|
|
|
11 |
2 |
0,2 |
I |
II |
|
|
|
10 |
6 |
0,15 |
|
I |
I |
|
|
011 |
3 |
0,1 |
|
|
II |
|
|
010 |
1 |
0,1 |
|
|
I |
I |
|
0011 |
9 |
0,05 |
II |
|
|
II |
|
0010 |
5 |
0,05 |
|
II |
|
I |
|
00001 |
7 |
0,03 |
|
|
II |
II |
I |
000001 |
8 |
0,02 |
|
|
|
|
II |
000000 |
Как
видно из таблицы 2.2, первый символ с
вероятностью
участвовал в двух процедурах разбиения
на группы и оба раза попадал в группу
с номером I . В соответствии с этим он
кодируется двухразрядным кодом II.
Второй элемент на первом этапе разбиения
принадлежал группе I, на втором – группе
II. Поэтому его код 10. Коды остальных
символов в дополнительных комментариях
не нуждаются.
Обычно неравномерные коды изображают в виде кодовых деревьев. Кодовое дерево – это граф, указывающий разрешенные кодовые комбинации [24]. Предварительно задают направления ребер этого графа, как показано на рис.2.10 (выбор направлений произволен).
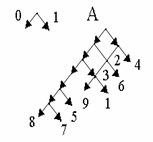
Рис. 2.1. Кодовое дерево для табл. 2.2
По графу ориентируются следующим образом: составляют маршрут для выделенного символа; количество разрядов для него равно количеству ребер в маршруте, а значение каждого разряда равно направлению соответствующего ребра. Маршрут составляется из исходной точки (на чертеже она помечена буквой А). Например, маршрут в вершину 5 состоит из пяти ребер, из которых все, кроме последнего, имеют направление 0; получаем код 00001.
Вычислим для этого примера энтропию и среднюю длину слова:
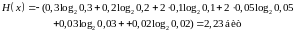
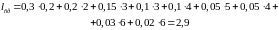
Как видно, средняя длина слова близка к энтропии.
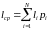