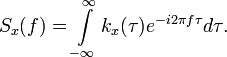26. Теорема Парсевалля применительно к случайным процессам. Пример использования для определения интервала дискретизации.

В статистической радиотехнике и физике при изучении детерминированных сигналов и случайных процессов широко используется их спектральное представление в виде спектральной плотности, которая базируется на преобразовании Фурье.

Если процесс x(t) имеет конечную энергию и квадратично интегрируем (а это нестационарный процесс), то для одной реализации процесса можно определить преобразование Фурье как случайную комплексную функцию частоты:

((1))

Однако она оказывается почти бесполезной для описания ансамбля. Выходом из этой ситуации является отбрасывание некоторых параметров спектра, а именно спектра фаз, и построении функции, характеризующей распределение энергии процесса по оси частот. Тогда согласно теореме Парсеваля энергия

((2))

Функция   характеризует, таким образом, распределение энергии реализации по оси частот и называется спектральной плотностью реализации. Усреднив эту функцию по всем реализациям можно получить спектральную плотность процесса.

Перейдем теперь к стационарному в широком смысле центрированному случайному процессу x(t), реализации которого с вероятностью 1 имеют бесконечную энергию и, следовательно, не имеют преобразования Фурье. Спектральная плотность такого процесса может быть найдена на основании теоремы Винера-Хинчина как преобразование Фурье от корреляционной функции:

((3))

Если существует прямое преобразование, то существует и обратное преобразование Фурье, которое по известной S_x(f) определяет k_x(τ):

((4))

Если полагать в формулах (3) и (4) соответственно f = 0 и τ = 0, имеем

((5))

((6))

Формула (6) с учетом (2) показывает, что дисперсия определяет полную энергию стационарного случайного процесса, которая равна площади под кривой спектральной плотности. Размерную величину S_x(f)df можно трактовать как долю энергии, сосредоточенную в малом интервале частот от f − df / 2 до f + df / 2. Если понимать под x(t) случайный (флуктуационный ток) или напряжение, то величина S_x(f) будет иметь размерность энергии [В²/Гц] = [В²с]. Поэтому S_x(f) иногда называют энергетическим спектром. В литературе часто можно встретить другую интерпретацию:   – рассматривается как средняя мощность, выделяемая током или напряжением на сопротивлении 1 Ом. При этом величину S_x(f) называют спектром мощностислучайного процесса.

Под теоремой Парсеваля обычно понимают унитарность преобразования Фурье. То есть сумма (или интеграл) квадрата функции равна сумме (или интегралу) квадрата результата преобразования. Следует заметить, что общий вид теоремы Парсеваля часто называют Теоремой Планшереля или Обобщенной формулой Рэлея.

Запись теоремы имеет вид

где   обозначает непрерывное преобразование Фурье, которое связывает временной или пространственный сигнал x(t) с его представлением в частотной области X(f).

В дискретном виде теорему записывают следующим образом:

,

где X(k) представляет собой дискретное преобразование Фурье сигнала x(k), имеющего N отсчетов.

Теорема Парсеваля устанавливает равенство между энергией сигнала и энергией его спектра.