5.Постановка задачи точечного оценивания параметра. Риск оценки (квадратичный). Понятие состоятельности, несмещенности, асимптотической нормальности оценки.

Постановка задачи точечного оценивания параметра. Риск оценки:

Пусть ( )- статистический эксперимент, результатом которого является набор наблюдений X₁…X_n. Задача точечного оценивания заключается в том, чтобы используя результаты наблюдений, выбрать из множества параметров θ значение, наиболее подходящее в том или ином смысле.

Пусть в качестве оценки параметра θ (или функции от пар-ра g(θ)) выбрана оценка .Для определения близости оценки к истинному значению пар-ра θ вводится функция потерь W(δ, θ) удовлетворяющая следующим условиям:

неотрицательность W(δ, θ)

если δ=0, то потери нулевые: W(θ, θ)=0

Наиболее употребительными функциями потерь являются W (δ, θ)=( δ - θ)² - функция потерь Гаусса и W(δ, θ)= |δ - θ| - функция потерь Лапласа.

Функция потерь – величина случайная, зависящая от двух параметров.

Точность оценки измеряется функцией риска R(δ, θ)=E_θ W(δ , θ), где E_θ берется при условии , что распределение соответствует значению параметра θ , т.е. средними потерями при оценивании с помощью δ.

Риск в случае функции потерь Гаусса R(δ, θ)=E_θ т.н. средне квадратичное отклонение

Хотелось бы найти оценку , минимизирующую риск при каждом значении θ. Однако в такой постановке задача неразрешима. Действительно, если выбрать в качестве оценки параметра θ некоторое постоянное значение δ = θ₀ , θ₀ , то при θ= θ₀ данная оценка абсолютно точна, т.е. имеет нулевой риск. Ясно , что подобная оценка с точки зрения матстатистики абсолютно бесполезна, однако приведённый пример показывает , что , за исключением тривиальных случаев (когда параметр определяется абсолютно точно), оценки , минимизирующей риск при каждом не существует.Для преодоления этой трудности можно ограничить класс рассматриваемых оценок:

рассматривать только состоятельные оценки

рассматривать только несмещенные оценки

Понятие состоятельности, несмещенности, асимптотической нормальности оценки:

Пусть имеется (Х, Д_n,Ρ), где Ρ={Р_θ,θєΘ} - статистический эксперимент.

Статистика - V отображение из Х в какое-то пространство Е (T: Х->E)

Отображение δ: Х->Θ точечная оценка параметра Θ (δ(х) – оценка параметра).

δ(х) можно сделать зависящей от n определенным образом δ(х)= δ_n(х) sdfg

Оценка δ(х) (в смысле δ_n(х)) называется состоятельной, если δ_n(х)-> θ ; V θєΘ по вероятности, т.е. Р_θ(|δ_n(х) – θ|>ε)->0 при n->∞.

Оценка сильносостоятельная, если Р_θ(δ_n(х) –> θ(почти наверное))->1

Оценка δ(х) называется несмещенной, если Е_θδ(х)= θ и асимптотически несмещенной если Е_θδ_n(х)-> θ при n->∞.

Асимптотически нормальна, если по распределению

6. Несмещенные оценки с равномерно-минимальной дисперсией. Минимаксный и байесовский подходы. Метод построения Байесовсих оценок.

Несмещенные оценки:

Оценка параметрической функции называется несмещенной , если при любом значении параметра

или просто

Смещением оценки называется величина .

Отметим что выборочная дисперсия не является несмещенной. С учетом независимости наблюдений (не умаляя общности считаем что ):

Тогда смещение . Нетрудно заметить что несмещенной оценкой дисперсии будет .

Несмещенная оценка не всегда может быть построена.Рассмотрим семейство распределений Пуассона. 1) θ= λ → -несмещенная оценка; 2)если Ограничимся одним наблюдением и построим несмещенную оценку:

, т.е. равенство не достижимо.

несмещенной оценки.

Риск несмещенной оценки совпадает с её дисперсией, поэтому если существует равномерно наилучшая из несмещенных оценок (т.е. имеющая наименьший среди всех несмещенных оценок риск при каждом значении ), то она называется несмещенной с равномерно минимальной дисперсией(НРМД).Т.е. , где δ^*- несмещ оценка.

Минимаксный и байесовский подходы. Метод построения Байесовсих оценок:

Оценка называется минимаксной если она минимизирует максимальный риск , т.е. или

Другой подход : Байесовский.

Пусть Q распределение задано на множестве

Байесовским риском оценки , с соответствующим функции потерь W, называется величина

Оценка минимизирующая байесовский риск, называется байесовской.

Пусть на задана (мера) вероятность , плотность которой (относительно доминирующей меры ) задается формулой , где - плотность р-ния θ, а - условная плотность р-ния при условии θ [ (- где - мера Лебега)],относительно некоторой доминирующей меры . Байесовский риск(функция потерь Гаусса)

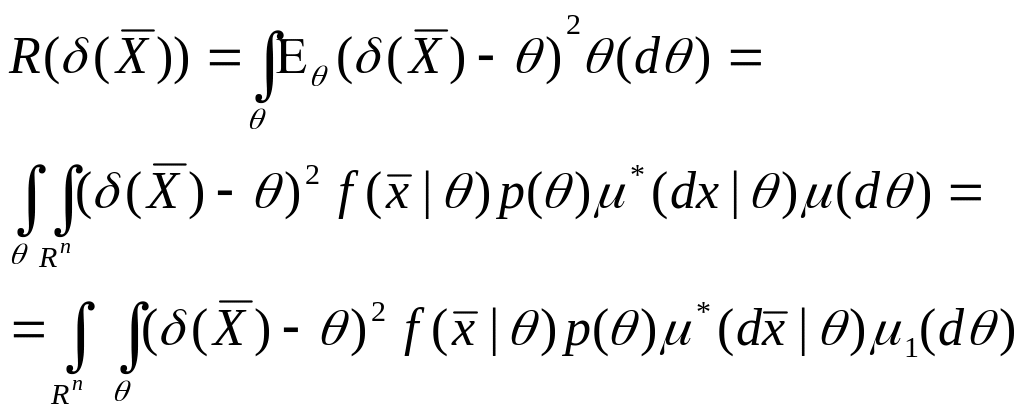
Найдем минимум этой функции по оценкам . Поскольку , фиксируем X, будем минимизировать интегральное выражение по d

Тогда -байесовская оценка.

Совместная плотность

Условная плотность (апостериорная)

- формула Байеса в непрерывном случае

-апостериорное матожидание при условии .